引言
通常使用的笛卡尔坐标系在某些情况下可能难以应用。其中一些最常见的情形包括存在圆形、圆柱形或球面对称性的场景。在这些情况下,使用其他坐标系往往更为便捷。
极坐标系
在极坐标系中,平面上的一个点由其到原点的距离 r 以及该点与原点连线和 x 轴之间的夹角 θ(以弧度为单位)确定(见下图)。
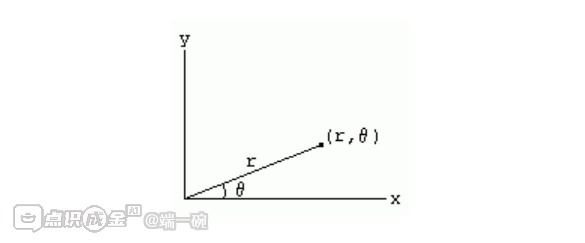
在极坐标系中,通常用有序对 (r, θ) 来表示一个点。利用标准的三角函数关系,我们可以推导出笛卡尔坐标系与极坐标系之间的转换公式:
- 从极坐标到笛卡尔坐标:
- x=rcosθ
- y=rsinθ
- 从笛卡尔坐标到极坐标:
- r=sqrt(x²+y²)
- θ=arctan(x/y)(需根据点所在象限调整角度值)
例子
具有直角坐标 (−1,0) 的点可以表示为极坐标 (1,π),而直角坐标 (3,−4) 的点对应的极坐标为 (5,−0.927)(其中 r=5 是距离原点的长度,θ≈−0.927 弧度对应第四象限的角度)。
极坐标的一个重要特性是:一个点可以有多种极坐标表示。以下是常见的情况:
- 角度的周期性
由于三角函数具有周期性,角度 θ 可以加上任意 2π 的整数倍,表示同一方向。例如:
$$
(r, \theta) \equiv (r, \theta + 2\pi n) \quad (n \in \mathbb{Z})
$$
- 负的半径 r
如果允许半径 r 为负数,则可以通过将 r 取相反数并调整角度 θ 加 π 来表示同一点:
$$
(r, \theta) \equiv (-r, \theta + \pi)
$$
- 原点的表示
当 r=0 时,无论 θ 取何值,都表示原点 (0,0)。
圆柱坐标系
圆柱坐标系是通过将笛卡尔坐标系中的 x 和 y 坐标替换为极坐标 r 和 θ(保持 z 坐标不变)而得到的。该坐标系特别适用于描述具有圆柱对称性或旋转对称性的问题。(本篇以数学方式将z作为向上的轴,游戏开发应把y作为向上轴)。

以下是圆柱坐标系与笛卡尔坐标系之间的转换关系:
从圆柱坐标到笛卡尔坐标
设圆柱坐标为 (r,θ,z),对应的笛卡尔坐标 (x,y,z) 为:
$$
\begin{cases}
x = r \cos\theta \
y = r \sin\theta \
z = z
\end{cases}
$$
从笛卡尔坐标到圆柱坐标
设笛卡尔坐标为 (x,y,z),对应的圆柱坐标 (r,θ,z) 为:
$$
\begin{cases}
r = \sqrt{x^2 + y^2} \
\theta = \arctan\left(\frac{y}{x}\right) \quad (\text{需调整象限}) \
z = z
\end{cases}
$$
示例
在笛卡尔坐标系中,点 (3,4,−1) 在圆柱坐标系中的表示为 (5,0.927,−1)。
类似地,对于函数的转换,利用上述转换关系,笛卡尔坐标系中的函数
f(x, y, z)
通过圆柱坐标系中的转换表示为
f(rcosθ, rsinθ, z)
球坐标系(Spherical Coordinates)
球坐标系是一种三维坐标系,通过三个参数 (ρ,θ,ϕ) 描述空间中的点,特别适用于具有球对称性或旋转对称性的问题。
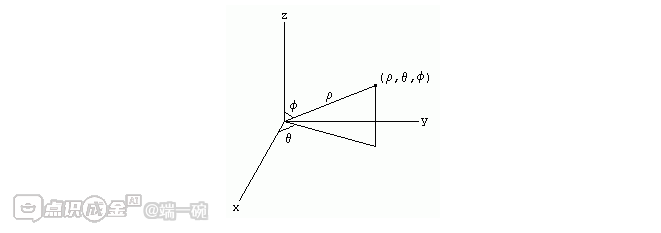
在球坐标系中,点的位置由三个参数表示:(ρ,θ,ϕ),其中:
- ρ:点到原点的距离(径向距离),ρ≥0
- θ:方位角(在 xy 平面内,从正 x-轴到点的投影与正 x-轴之间的夹角),0≤θ<2π
- ϕ:极角(从正 z-轴到点的连线与正 z-轴之间的夹角),0≤ϕ≤π
从球坐标 (ρ,θ,ϕ) 到笛卡尔坐标 (x,y,z) 的转换公式:
$$
\begin{cases}
x = \rho \sin\phi\cos\theta \
y = \rho \sin\phi\sin\theta \
z = \rho \cos\phi
\end{cases}
$$
以下是笛卡尔坐标 (x,y,z) 到球坐标 (ρ,θ,ϕ) 的转换公式:
$$
\begin{cases}
\rho = \sqrt{x^2 + y^2 + z^2} \
\theta = \arctan\left(\frac{y}{x}\right) \quad (\text{需调整象限}) \
\phi = \arctan\left(\frac{\sqrt{x^2 + y^2}}{z}\right)
\end{cases}
$$
从球坐标到圆柱坐标的转换关系
球坐标系 (p,θ,ϕ) 与圆柱坐标系 (r,θ,z) 之间的转换关系如下:
$$
\begin{cases}
r = p \sin\phi \
\theta = \theta \
z = p \cos\phi
\end{cases}
$$
从圆柱坐标到球坐标的转换关系
圆柱坐标系 (r,θ,z) 与球坐标系 (p,θ,ϕ) 之间的转换公式如下:
$$
\begin{cases}
p = \sqrt{r^2 + z^2} \
\theta = \theta \
\phi = \arctan\left(\frac{r}{z}\right)
\end{cases}
$$