上篇实验我们对2D极坐标系已经有过了解,这篇实验主要对极坐标系进行实践
案例的完整代码如下:
mat2 roatate2d(float theta) {
return mat2(cos(theta), -sin(theta),
sin(theta), cos(theta)
);
}
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
vec2 uv = 2.*(2.* fragCoord - iResolution.xy)/iResolution.y;
uv = roatate2d(iTime) * uv;
float r = atan(uv.y, uv.x);
float d = 0.5 + sin(r * 3.) * 0.5;
d = pow(d, 0.4);
float d2 = 0.5 + cos(r * 6.) * 0.15;
d += d2;
float v = smoothstep(d, d-0.01, length(uv));
float h = length(uv)/d;
vec4 col = mix(vec4(1.), vec4(0.5*h,.5*h+0.5,0.,1.), v);
// Output to screen
fragColor = col;
}
部分代码在2D极坐标系中有过讲解。
这里主要对如下代码进行分析:
float r = atan(uv.y, uv.x);
float d = 0.5 + sin(r * 3.) * 0.5;
d = pow(d, 0.4);
float d2 = 0.5 + cos(r * 6.) * 0.15;
d += d2;
float h = length(uv)/d;
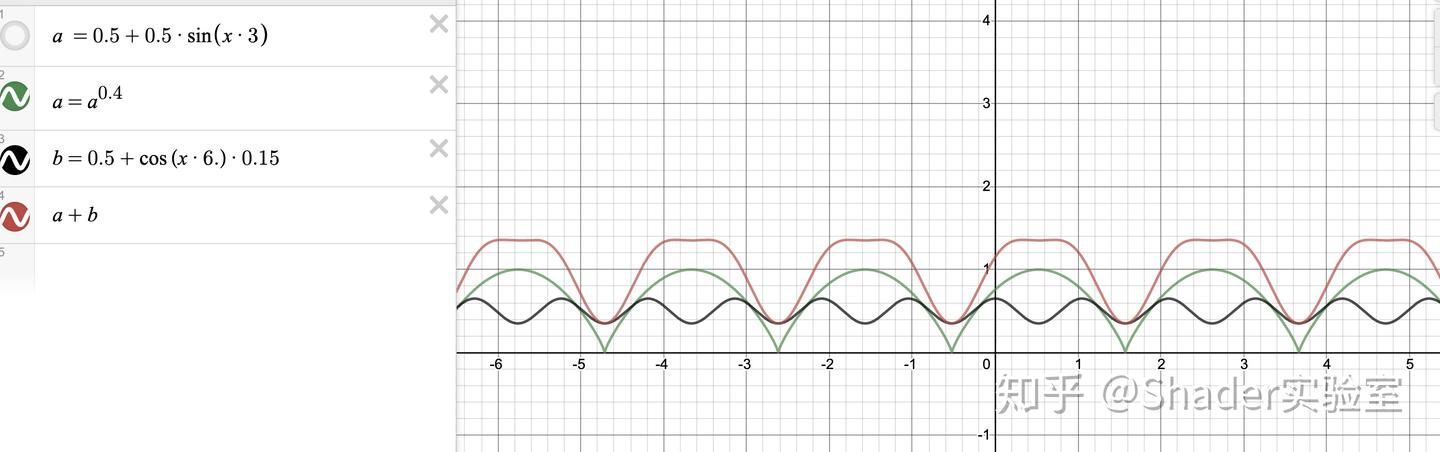
对d与d2值的相加操作可作图如下:
转为极坐标系图示如下:
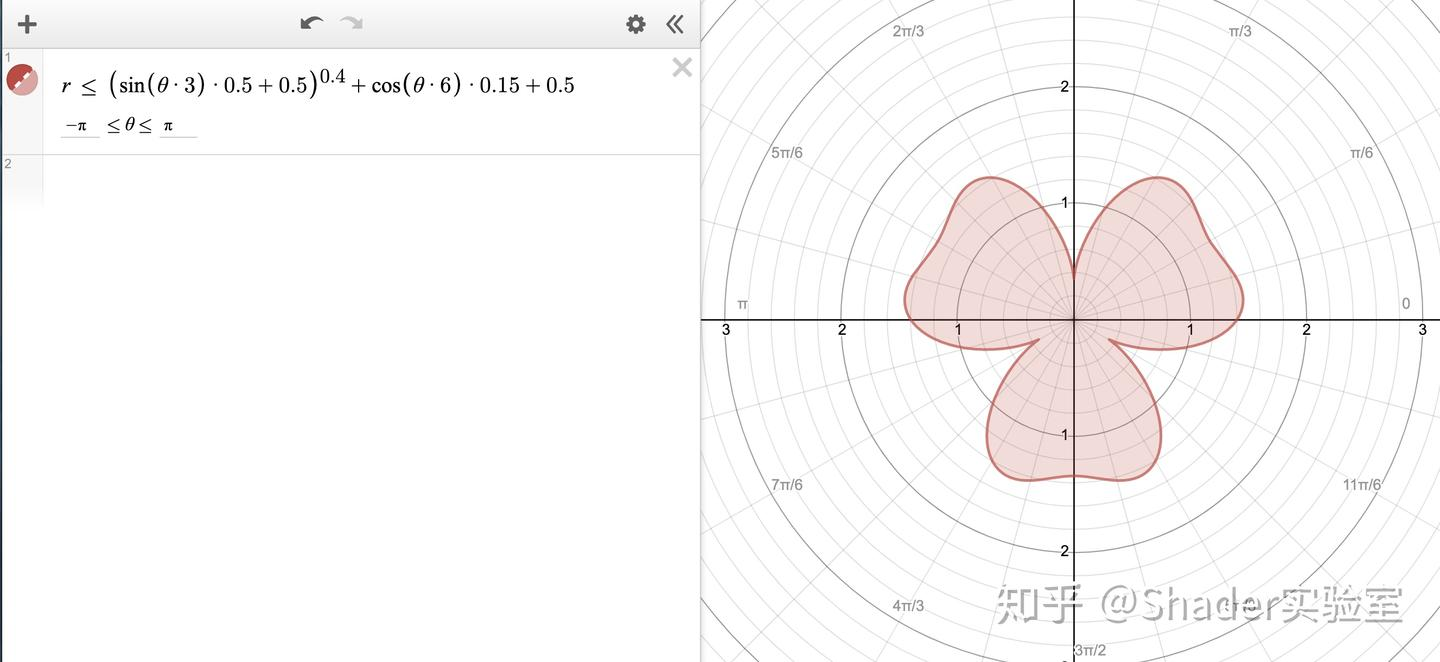
知道运作原理后,再分析下颜色渐变的实现,由于length(uv)是由中间往四周由小变大的方式扩散,而d值的映射是笛卡尔坐标系红色线的结果,通过length(uv)/d得出的结果作用于最终颜色上,很容易得出最终的映射结果。

感兴趣的伙伴可关注知乎"Shader实验室"或扫描下方二维码关注公众号
