2D极坐标系

Question

笛卡尔坐标系不是精确绘制空间和定义位置的唯一系统，笛卡尔系统的替代方案是极坐标系。本篇内容主要讨论的是二维极坐标系，关于三维极坐标系会在后续实验中继续讨论。

原理

与2D笛卡尔坐标系通过原点与两个穿过原点的轴来确立坐标系类似，2D极坐标系也有一个原点，称为极点，极点定义了坐标空间的“中心”。不同的是极坐标空间只有一个轴，通常称之为极轴，极轴常被用来描述为经过极点的射线。

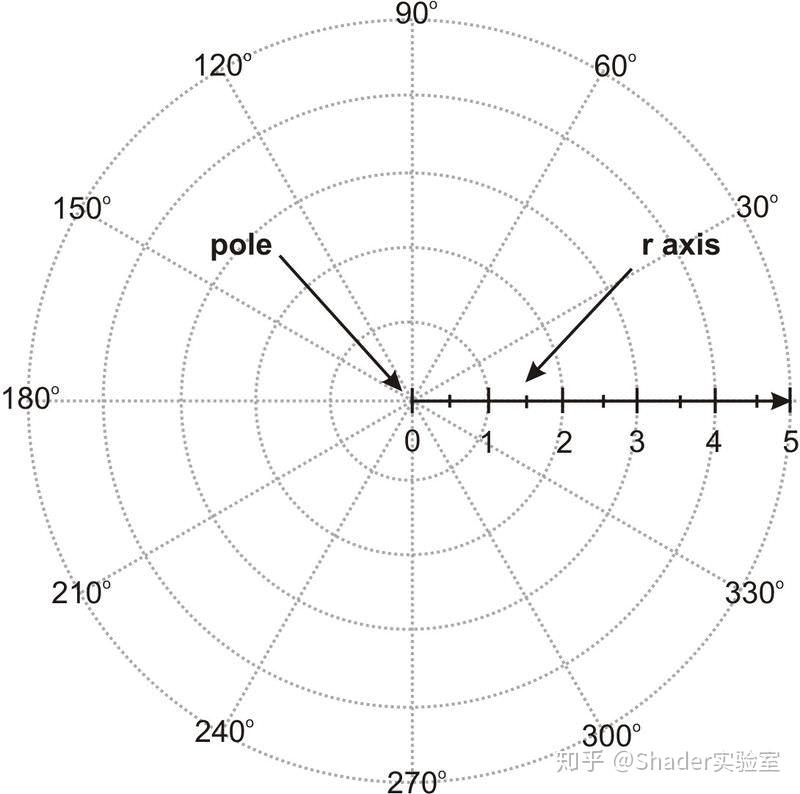
在笛卡尔坐标系中，通常使用两个有符号距离x和y来描述一个二维点，而极坐标系中通过距离r与角度θ来描述一个坐标点，通常用(r, θ)表示。

定位极坐标点(r, θ)需要两个步骤：

1.从极点开始，朝向极轴方向，并旋转角度θ，θ的正值通常被定义为沿逆时针旋转，反之负值就沿顺时针旋转。

2.通过步骤1确定的角度，从极点向前移动r个单位的距离，即可得到极坐标点(r, θ)。

总结上述步骤为：r定义了该点到极点的距离，θ定义了从极点开始的点的方向。

注：由于θ是一个角度值(计算机运算时需把角度转弧度),涉及到角度运算，必然有无数个可以重合的角度，比如
180°与540°等类似角度都代表着相同方向，这里我们不做过多讨论，这只是不同角度的相同方向表达。有些书籍
会对极坐标的坐标点进行规范化，如规定r需要大于0，角度限定范围为-180°~180°，r=0时θ对应也为0等，在
shader开发中，规范化坐标不做必要求取。

2D笛卡尔坐标与极坐标间的相互转换：

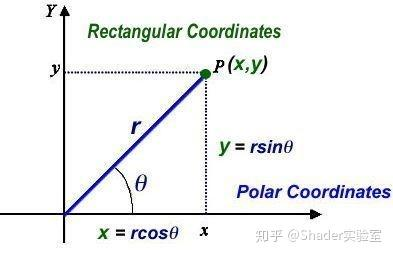
上图已经能完整表达笛卡尔坐标与极坐标的相互转换，将极坐标(r, θ)变换为相应的笛卡尔坐标，几乎可以立即得出正弦和余弦与笛卡尔坐标的关系。

x = r * cos(θ);
y = r * sin(θ);

如果已知笛卡尔坐标(x, y)要转为极坐标(r, θ)的方式也很简单：

// 通过毕达哥拉斯定理求取r
r = sqrt(x²+y²)

r已经能够正确求取了，剩下的工作就是求取θ，可通过下面的方式求取：

y/x = rsin(θ)/rcos(θ);
y/x = sin(θ)/cos(θ);
y/x = tan(θ);
θ = arctan(y/x);

表面上看θ已经能顺利求取了，但是这种方式存在两个问题：

1.当x为0时，算式未定义；

2.由于y与x为有符号值，容易受不同象限y与x的正负影响，求取的θ的结果为[-π/2, π/2]。

实际上上述结果的求取等效于glsl中atan函数的定义，

type atan (type y_over_x);

为了解决上述遇到的问题，glsl api为我们提供了另一个函数:

type atan (type y, type x);

通过传递相应的y与x值，即可得到[-π, π]的范围值，还可避免除0的问题，这是我们需要的。

atan(type y, type x) 的实现思路大体如下（注：这里以角度为例，实际开发以弧度为准）：

当x = 0，y = 0时， 结果为0°；
当x = 0, y > 0时， 结果为90°；
当x = 0，y < 0时， 结果为-90°；
当x > 0, 结果为arctan(y/x);
当x < 0, y >= 0, 结果为arctan(y/x) + 180°
当x < 0, y < 0, 结果为arctan(y/x) - 180°

实验

通过Shadertoy编写如下代码：

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
    // Normalized pixel coordinates (from 0 to 1)
    vec2 uv = fragCoord/iResolution.xy;
    // 将坐标中心从左下角移至中心
    uv -= 0.5;
    // atan(uv.y, uv.x)求取范围为-π~π，加上π的范围为0~2π
    fragColor = vec4(atan(uv.y, uv.x) + PI);
}

图像输出如下：

上述效果只考虑了把笛卡尔坐标(x, y)转为θ的过程，现在把极轴r的距离考虑进来，做个简单花瓣效果，代码如下：

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
    // Normalized pixel coordinates (from 0 to 1)
    vec2 uv = fragCoord/iResolution.xy;
    // 坐标转为-1 ~ 1,坐标原点为中心位置
    uv = (uv - 0.5) * 2.;
    // atan求取的θ值作为正弦的弧度值，求取的结果作为极轴的距离
    // 此时atan的结果为-π ~ π
    float r = sin(atan(uv.y, uv.x));
    // 通过(uv.x, uv.y)的长度与极轴的距离做对比
    float v = smoothstep(r, r+0.01, length(uv));
    // Output to screen
    fragColor = vec4(v);
}

图像结果如下：

相信很多伙伴不太理解图像会什么会这么形成，这里我做了下图进行分析：

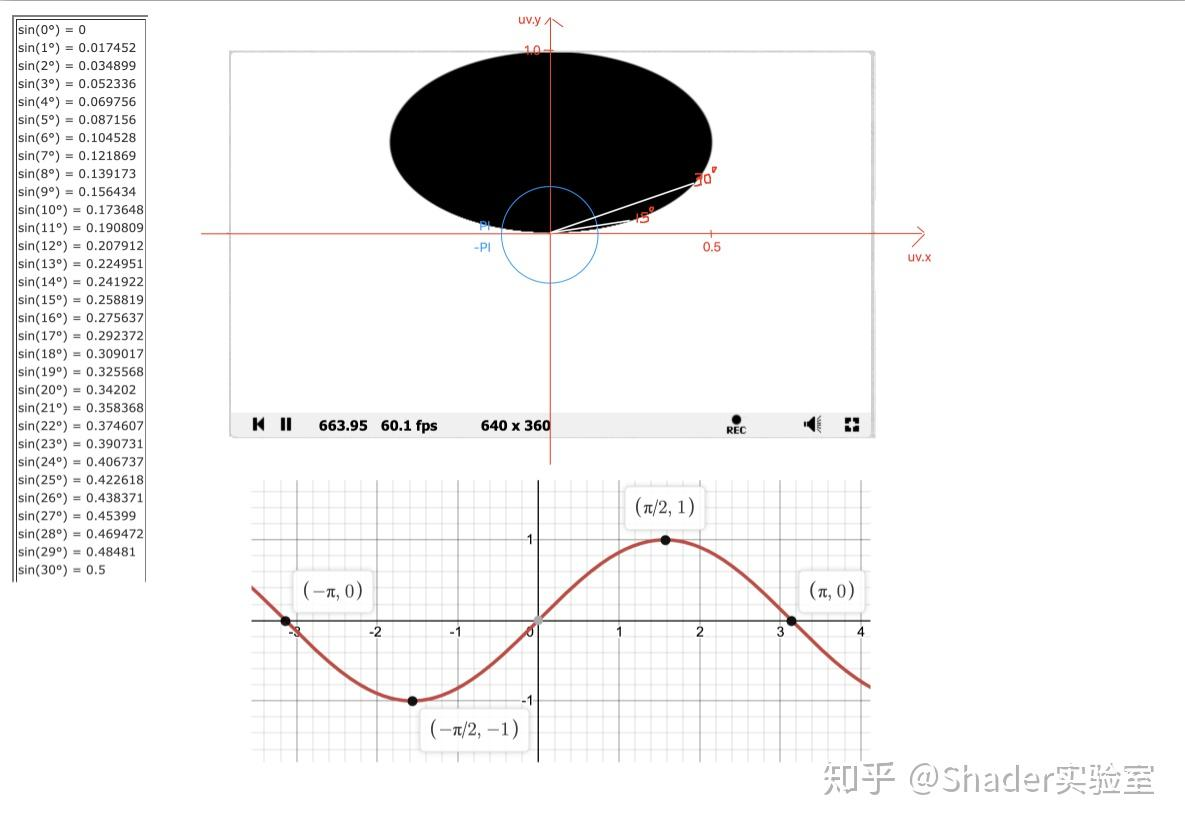
图像只形成于上半部的原因是因为atan的结果范围为[-π，π]，当atan结果小于0时，正弦的最终结果都为负值，但是length(uv)的结果为非负值，所以屏幕下半部分没有图像输出，上半部分的图像可结合正弦值的表与正弦图像，很容易进行相应映射。

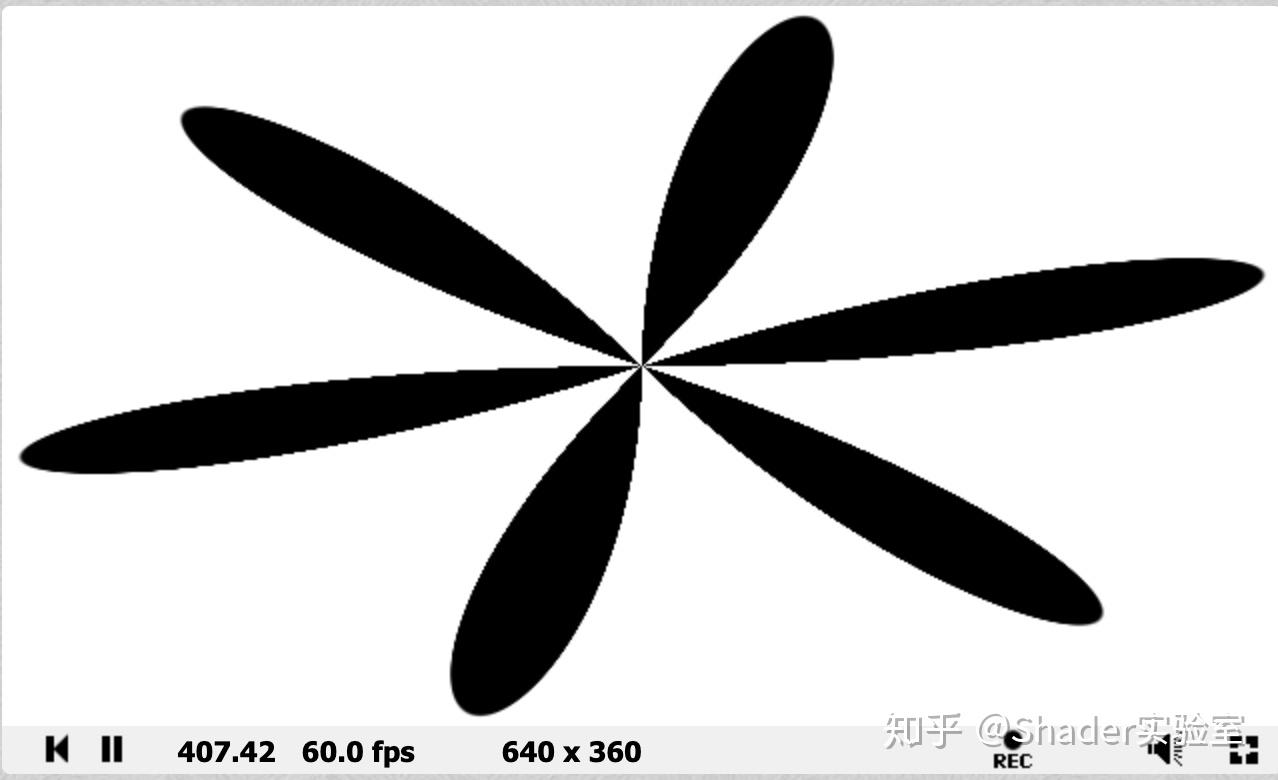
分析原理后，可适当修改代码，即可得到简单的花瓣形效果：

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
    // Normalized pixel coordinates (from 0 to 1)
    vec2 uv = fragCoord/iResolution.xy;
    // 坐标转为-1 ~ 1,坐标原点为中心位置
    uv = (uv - 0.5) * 2.;
    // atan求取的θ值作为正弦的弧度值，求取的结果作为极轴的距离
    // 原本atan的结果为-π ~ π
    // 这里乘上6，那么此时范围就为-6π~6π
    float r = sin(atan(uv.y, uv.x) * 6.);
    // 通过(uv.x, uv.y)的长度与极轴的距离做对比
    float v = smoothstep(r, r+0.01, length(uv));
    // Output to screen
    fragColor = vec4(v);
}

结合正弦函数：

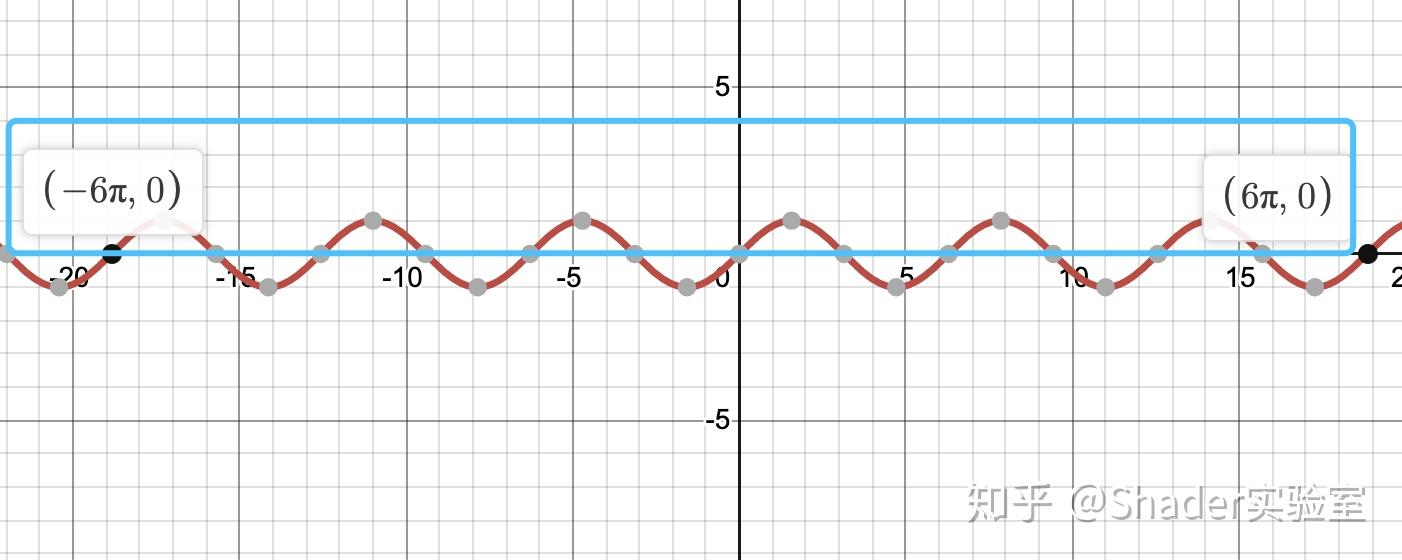
此时大于0的”驼峰“共6个，那花瓣数量必然为6：

感兴趣的伙伴可关注下方二维码：

2D极坐标系

原理

实验

0 Answers