Shader实验室: smoothstep函数

Question

smoothstep可以用来生成0到1的平滑过渡值，它也叫平滑阶梯函数

上图演示的是通过smoothstep产生的距离场(Distance Field)效果，它是smoothstep函数的一个简单实现，同样smoothstep也符合重映射(可查阅Shader实验室: remap函数)的定义。

原理

smoothstep公式定义如下(通过源码分析)：

float smoothstep(float t1, float t2, float x) {
  // Scale, bias and saturate x to 0..1 range
  // 还记得么？在remap算法中接触过
  x = clamp((x - t1) / (t2 - t1), 0.0, 1.0); 
  // Evaluate polynomial
  return x * x * (3 - 2 * x);
}

根据上式，我们找些数字代入，假设 t1 = -2，t2 = 3:

y = (x - (-2)) / (3 - (-2)) 。且 result = y * y * (3 - 2 * y)。

x还是取两个特殊值，分别为-2，3；

当x=-2，y=0，result = 0；

当x=3，y=1，result = 1；

此时可以作图如下：

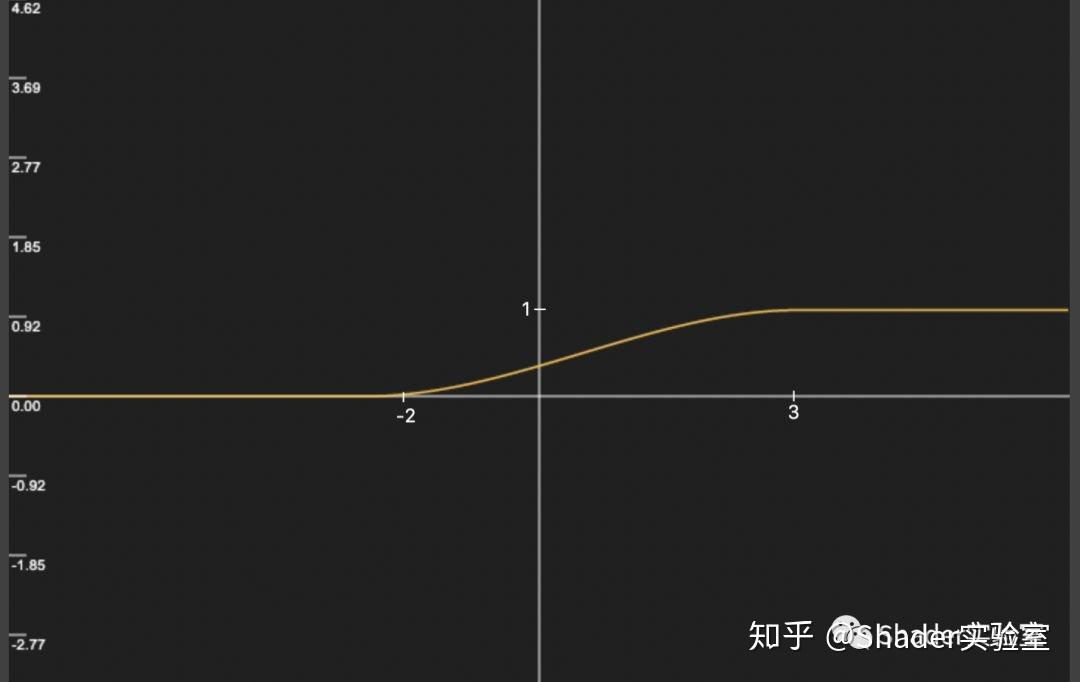
可以看出，x在 t1 到 t2 值的范围内变化曲线由缓到快再到缓的过程，并且我们可以得出结论：

当x等于t1时，结果值为0；

当x等于t2时，结果值为1；

(ps: 值限制在0~1之间的原因是因为clamp函数的限制)

为了验证得出的结论并有个与结论对应的效果，我们交换t1与t2的值，也就是此时t1 = 3，t2 = -2，作图如下：

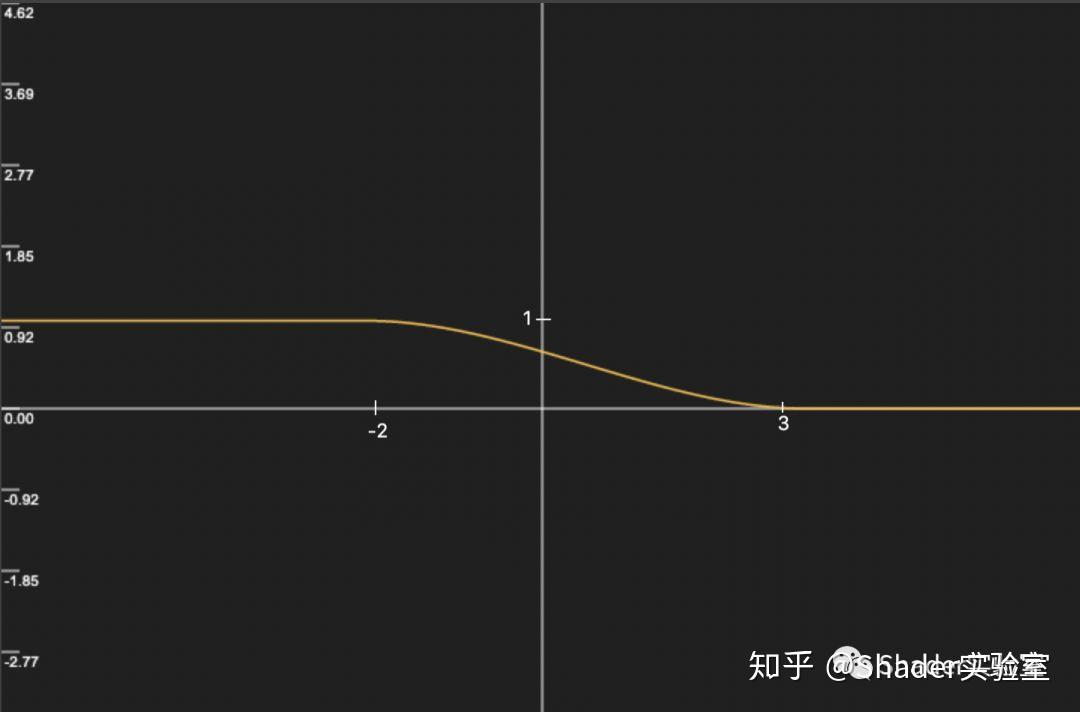
结合图像可知：
当x = t1 = 3时，结果值为0；
当x = t2 = -2时，结果值为1；

它再次验证了我们的结论，并且t1与t2值的位置也显得尤为重要，它决定了曲线变化的走向，请大家一定要记住该结论，并将它结合到我们的实际开发中。
我们已经分析了smoothstep函数的内部实现与原理，那么有一个问题不知道大家是否想过，假设有两个smoothstep函数(参数t1值都小于t2值)，第二个smoothstep的t1值正好等于第一个smoothstep的t2值，并且两个smoothstep进行了相减操作，结果会如何：

假设第一个为：smoothstep(1, 2, x)；

第二个为：smoothstep(2, 3, x);

作图如下：

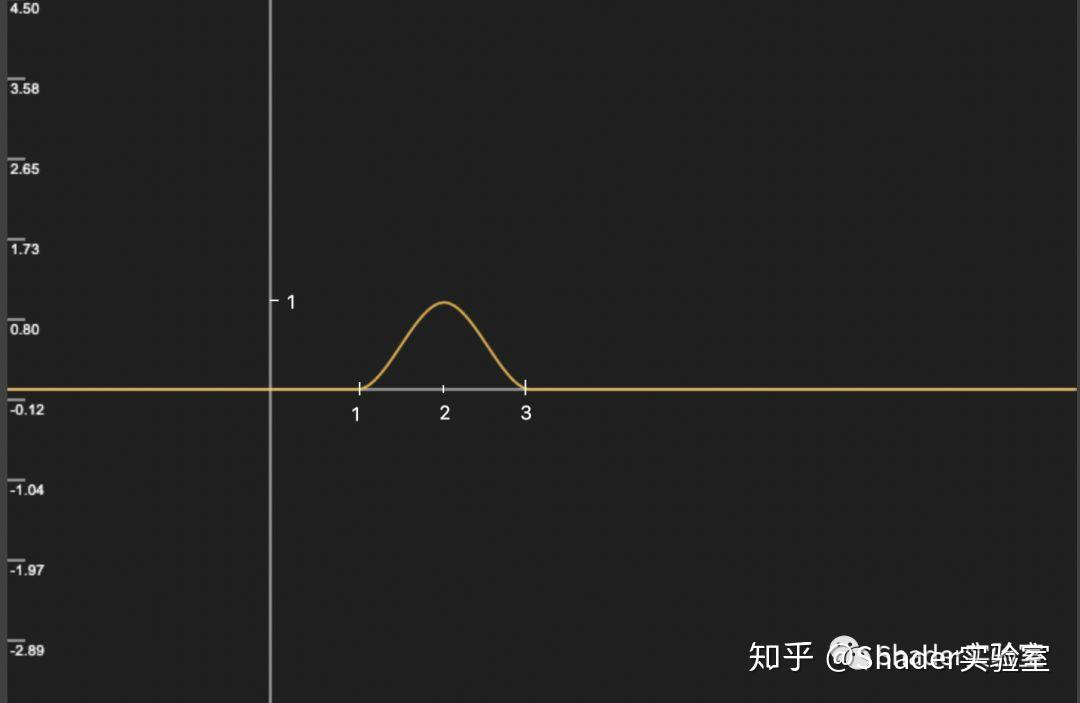
根据结果可知，示例中的两个smoothstep进行相减操作时，在x的值为2时达到了峰值，并会往两边递减。

那如果我们把第二个smoothstep改为：
smoothstep(3, 4, x)结果又会如何呢？

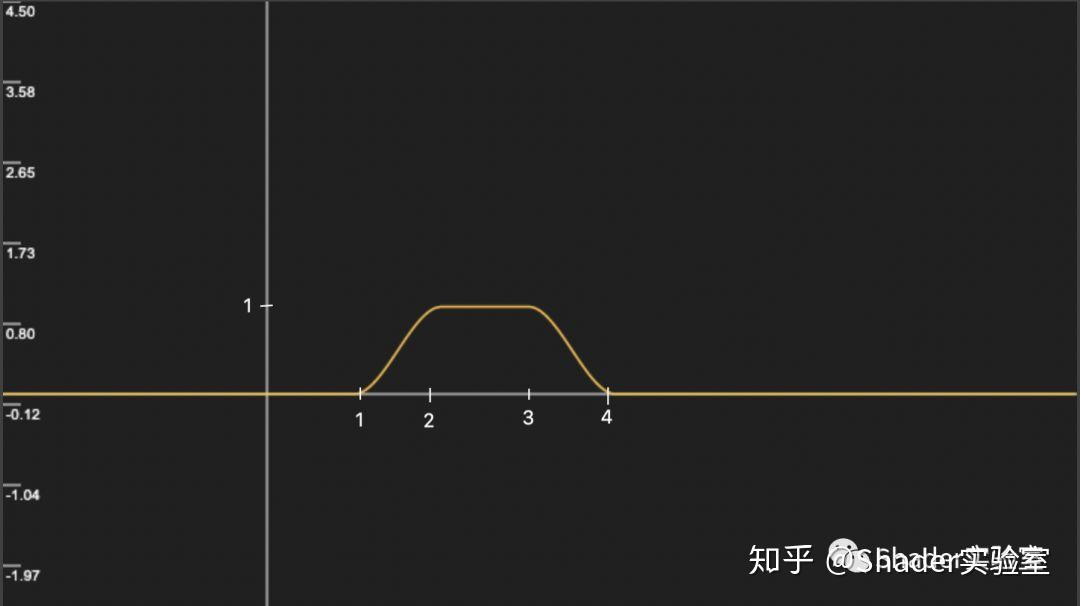
同样的，峰值依旧会在第一个smoothstep中的t2值与第二个smoothstep中的t1值之间产生，并随之会往两边递减。

这也是我们在开发中经常会直接用到的结论，在实验部分我们也会用这个结论做一个圆环效果。

实验

新建Unlit Shader与Material。
打开Unlit Shader文件，并修改frag函数：

fixed4 frag (v2f i) : SV_Target
{
   // 先把uv坐标原点从左下角移至中心位置
   // 通过length计算点（uv.x，uv.y）到原点的距离
   // x大于等于t1=0.5时，结果为0
   // x小于等于t2=0.2时，结果为1
   return smoothstep(0.5, 0.2, length(i.uv - 0.5));
 }

3.呈现的效果如下：

实现圆环，修改frag代码如下：

fixed4 frag (v2f i) : SV_Target
{
    half l = length(i.uv - 0.5);
    float s1 = smoothstep(0.2, 0.3, l);
    float s2 = smoothstep(0.3, 0.4, l);
    return s1 - s2;
}

最终效果。

对Shader开发感兴趣的话，可一起关注下面的二维码噢。

Shader实验室: smoothstep函数

原理

实验

0 Answers