本教程将开启逆向运动学的探索。虽解法众多,但皆始于正向运动学。
核心概念对比
- 逆向运动学(IK):给定空间目标点,求解如何运动肢体才能抵达该点
- 正向运动学(FK):已知肢体运动参数,计算末端在空间中的最终位姿
二者构成运动学中互为对偶的双向问题。
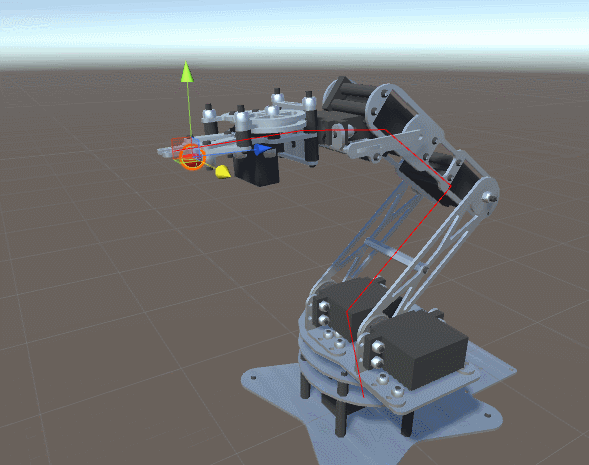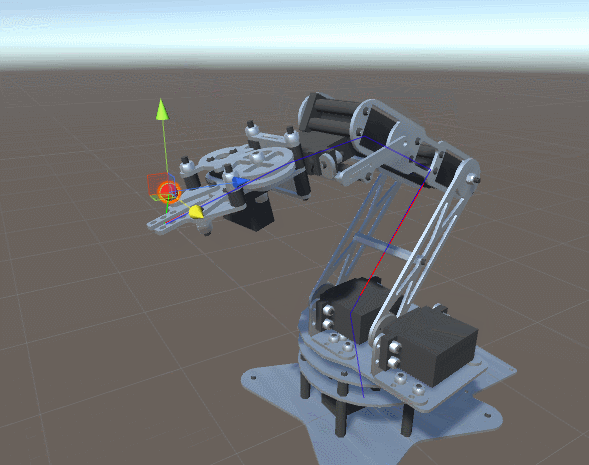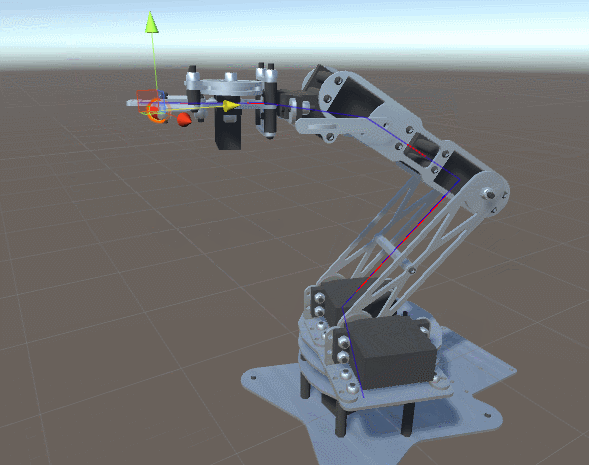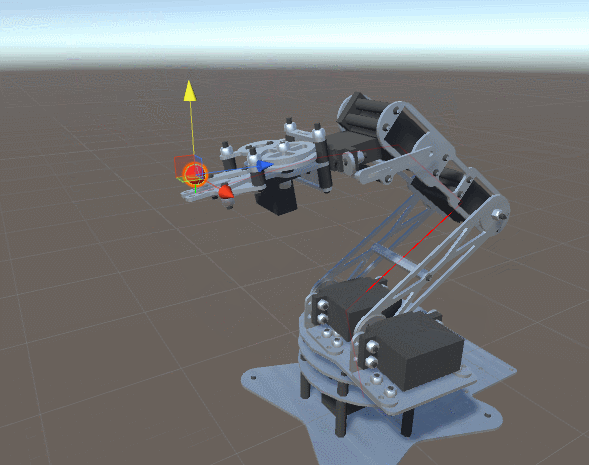
机械臂
尽管本教程使用机器人学术语,但IK技术同样适用于生物运动模拟(如人体、蜘蛛肢体、触手等)。首先明确机械臂的核心组成:
-
基座(Base)固定于参考坐标系的原点,提供运动基准
-
连杆(Links)刚性结构部件,通过关节串联构成运动链
-
关节(Joints)
- 旋转关节(Revolute):绕单轴转动(1自由度)
- 平移关节(Prismatic):沿单轴滑动(1自由度)
-
末端执行器(End Effector)
最终执行操作的部件(如夹爪、焊枪)
此结构定义虽源自工业机器人,但其数学框架可泛化至各类生物/虚拟运动系统。

上面的图片展示了一个典型的机器人手臂,由“肢体”通过“关节”连接而成。由于图中的机器人手臂有五个独立的关节,因此被称为具有五个自由度。每个关节由一个电机控制,允许连接的连杆旋转到一定的角度。
为了得出通用性的结论,我们可以绘制出关节的精确结构图。在本教程中,我们将假设每个关节只能在单一轴上旋转。
 在机器人手臂末端的工具被称为末端执行器(end effector)。根据具体情况,是否把它纳入自由度考量取决项目本身。在本教程中,我们将不考虑末端执行器,因为我们将专注于机械臂运动本身。
在机器人手臂末端的工具被称为末端执行器(end effector)。根据具体情况,是否把它纳入自由度考量取决项目本身。在本教程中,我们将不考虑末端执行器,因为我们将专注于机械臂运动本身。
正向运动学
在此简化示例中,每个关节可绕特定轴旋转,其状态由旋转角度度量。通过调整各关节至特定角度,末端执行器将抵达空间中不同位置。正向运动学的任务是:在已知所有关节角度的前提下,计算末端执行器的空间坐标。
正向运动学属于"简单"问题,即每个角度组合对应唯一确定且无歧义的计算结果。理解机械臂如何响应电机输入的运动规律,是求解其逆向运动学对偶问题的必要基础。
几何直观解析
在编写代码前,需从数学与空间几何层面理解正向运动学。鉴于3D旋转的复杂性,我们从2D平面机械臂入手分析。机械臂存在基准姿态——所有关节处于零角度旋转的位姿,这是后续运动分析的初始参考状态。
 上图展示了一个三自由度机械臂。当所有关节处于零角度时,系统处于基准姿态(初始构型)。若绕P₀节点旋转α₀度,将导致与之相连的关节与连杆链产生联动。这种运动传递效应可分解为:
上图展示了一个三自由度机械臂。当所有关节处于零角度时,系统处于基准姿态(初始构型)。若绕P₀节点旋转α₀度,将导致与之相连的关节与连杆链产生联动。这种运动传递效应可分解为:
 需注意,其他关节的驱动电机还未有其它动作。每个关节仅仅驱动其后续连杆链进行局部的旋转。下图展示了当第二关节旋转α₁角度时机械臂的位姿变化。
需注意,其他关节的驱动电机还未有其它动作。每个关节仅仅驱动其后续连杆链进行局部的旋转。下图展示了当第二关节旋转α₁角度时机械臂的位姿变化。

旋转参考系的累积效应需明确:
- P₁位置:仅由基关节α₀决定
- P₂位置:同时受α₀(基关节)与α₁(第二关节)的双重影响
坐标系定向规则:
- 每个关节的局部坐标系(红/蓝箭头)方向由前方关节旋转总和确定
- 示例:第二关节的旋转参考系 = 基关节旋转α₀后的坐标系(本地坐标系)
这种链式参考系传递机制,正是多关节系统实现复杂空间运动的核心数学基础。
数学解析
从前面的图示可以明确看出,要解决正向运动学问题,我们需要能够计算因旋转而嵌套的物体位置。
让我们以双关节系统为例说明计算方法。一旦解决了双关节问题,我们只需按顺序推广即可解算任意长度的关节链。
让我们从简单情况开始:假设第一个关节处于起始位置(即基关节角度α₀=0),其初始状态如下图所示:
 简而言之:
简而言之:
$$
P_1 = P_0 + D_1
$$
当α₀不为零时,需将静止状态下的距离向量D₁绕点P₀旋转α₀角度:

数学上我们可以这样写:
$$
P_1 = P_0 + rotate(D_1, P_0, α_0)
$$
后续将展示如何通过 AngleAxis函数(Unity文档)实现旋转运算,无需手动处理三角函数。
位姿方程推导:
套用相同逻辑,P₂的坐标可通过以下公式解算:
$$
P_2 = P_0 + R(\alpha_0) \cdot \left( D_1 + R(\alpha_1) \cdot D_2 \right)
$$
- ( R(α1)与 R(α2)) 为绕Z轴的旋转矩阵(2D场景)
- ( D1, D2 ) 为各连杆在基准姿态下的原始向量
最后得到通用的一般式:

Unity 已内置实现上述所有需求的功能:父子级关系。将一个游戏对象设为另一个对象的子级时,会自动继承父级的位置、旋转和缩放。
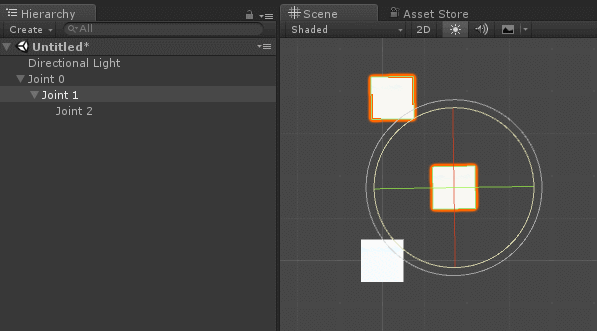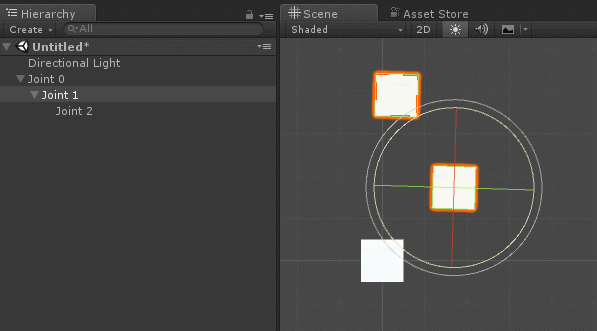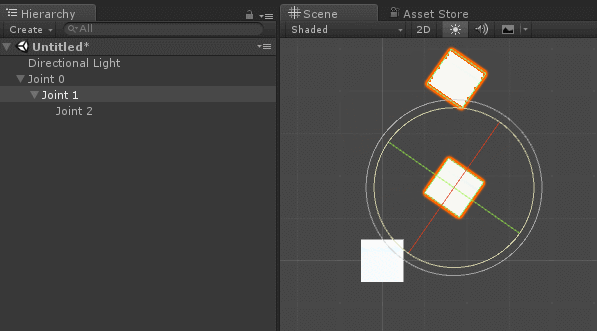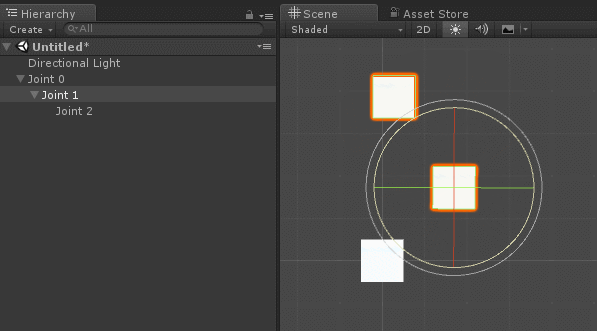
熟悉角色骨骼绑定的开发者对此应不陌生(Shader实验室的骨骼动画原理已有介绍)。在人体角色骨骼系统中,关节骨骼会以父子级关联的方式设置,使得旋转与位移属性能够被继承。如下图:

在创建机械臂关节层级时,需确保当所有本地欧拉角(Local Euler Angles)归零时,机械臂处于基准静止姿态。这类似于人形角色绑定中的T-Pose(见上图),此时所有骨骼处于无旋转的初始对齐状态。
《底特律:变人》中的仿生人关节系统即严格遵循此规范——所有机械关节的零角度姿态均对应工业设计图纸的展开状态,确保动画师可基于此基准姿态进行关键帧创作。
实现方案
Unity 的父子层级系统实际上已为我们解决了正向运动学问题。但遗憾的是,这仍不足够。在本教程后续关于梯度下降逆向运动学的部分中,我们将看到需要在不实际移动机械臂的情况下测试末端执行器位置的需求。这迫使我们必须重新在 Unity 中实现此基础功能。
第一步
需在机械臂的每个关节上存储特定信息。可通过添加脚本实现(如下方示例的 RobotJoint 脚本):
using UnityEngine;
public class RobotJoint : MonoBehaviour
{
public Vector3 Axis;
public Vector3 StartOffset;
void Awake ()
{
StartOffset = transform.localPosition;
}
}
你应该为每个用作机械臂关节的游戏对象添加 RobotJoint 脚本。每个你希望由 IK 系统旋转的游戏对象都应该附加这样一个脚本。
为了简化计算,我们假设每个关节只能绕其局部的一个轴旋转:X、Y 或 Z 轴。我们通过一个名为 Axis 的变量来表示这一点,该变量在相对于旋转轴的位置有一个值为 1。如果这个关节绕 Y 轴旋转,那么 Axis 就是 (0,1,0)。稍后我们会看到这如何帮助我们避免使用 IF 语句。
实际的 IK 代码应该存储在一个不同的脚本中,这个脚本将作为“IK 管理器”。你可以把它放在机械臂的根节点中,不过它放在哪里其实并不重要。它的作用是执行正向运动学和逆向运动学。为此,管理器脚本需要知道关节在哪里。这可以通过将它们存储在一个 RobotJoint 类型的数组或列表中实现,这个数组或列表将被称为 Joints。
管理器脚本需要一个名为 ForwardKinematics 的函数。它接受一个浮点数数组作为输入,这个数组被称为 angles。顾名思义,angles[i] 包含了 Joints 列表中第 i 个关节的局部旋转角度。该函数返回末端执行器在全局坐标中的位置。
public Vector3 ForwardKinematics (float [] angles)
{
...
}
这段代码是之前看到的关于计算末端效应器位置方程的 C# 实现。rotate 函数则是通过Unity内置的 Quaternion.AngleAxis 来实现的。
Vector3 prevPoint = Joints[0].transform.position;
Quaternion rotation = Quaternion.identity;
for (int i = 1; i < Joints.Length; i++)
{
// Rotates around a new axis
rotation *= Quaternion.AngleAxis(angles[i - 1], Joints[i - 1].Axis);
Vector3 nextPoint = prevPoint + rotation * Joints[i].StartOffset;
prevPoint = nextPoint;
}
return prevPoint;