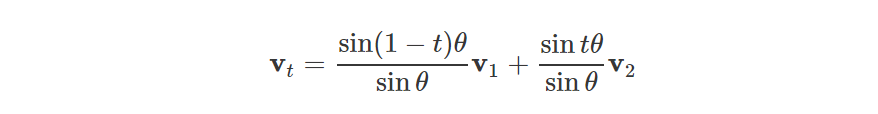在四元数与旋转中，我们看到如下的向量间的球面插值公式：
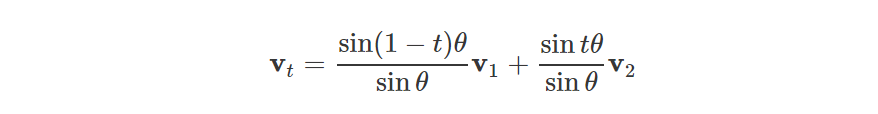
通过上述式子，引出两四元数间的球面插值公式：
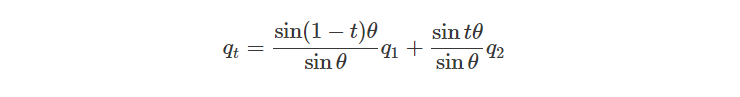
在游戏开发的背景下，slerp 通常对四元数表示的方向进行插值操作，而四元数可以表达为4D向量。在这种情况下，slerp 所沿的最短弧位于一个4D超球面上。
而开篇的公式可以用于任何维度高于1D的向量间的插值。因此，它也可以用来沿着球面对两个3D向量进行插值，或沿着圆周对两个2D向量进行插值。
在游戏开发的情境中，我们几乎只使用单位四元数。因此，在如下的推导过程中，假设我们处理的向量都是单位向量。即使向量不是单位向量，推导的过程也应该大致相同。
如下图所示，有两个向量v0与v1，两向量间的夹角为θ，vt向量是插值过程中的结果向量，vt与v0的夹角为tθ，vt与v1的夹角为(1-t)θ, 所以我们要求取的是vt向量：
对于vt，我们可以通过：
$$
v_t=av_0+bv_1
$$
剩下的就是求取a与b的值。我们先求取b，过vt末端作v0的垂线，且垂线过O点：
所以线段vtO的长度为：
$$
sin(tθ) = {{线段v_to}\over{|v_t|}}
$$
而|vt|的值为1(单位向量)，所以线段 vtO=sin(tθ)，而∠bv1v0的角度为θ(平行v1)，所以：
$$
sin(θ)={线段v_to \over b|v1|}={sin(tθ) \over b|v1|}
$$
因为|v1|等于1，所以b就等于：
$$
b={sin(tθ) \over sin(θ)}
$$
接下来求取a的值，求取方式与上述方法一致，我们移除无关的线段标注：
根据上图，我们得到：
$$
sin((1-t)θ)={线段v_to \over |v_t|}
$$
所以：
$$
线段v_to=sin((1-t)θ)
$$
又因为 ∠vtAO=θ，所以：
$$
sin(θ)={线段v_tO \over a|V_0|} = {sin((1-t)θ) \over a}
$$
所以最后就能求得a的值为：
$$
a={sin((1-t)θ) \over sin(θ)}
$$
所以vt的求取结果就如下公式所示：
