菲涅尔效应原理与实现

Question

当光从一种折射率为n1的介质向另一种折射率为n2的介质传播时，在两者的交界处可能会同时发生光的反射和折射

介绍

我们时常会去湖边散步，不知有没有看过一个现象：同一个地方的湖面，在不同的位置去观察它，总能看到它在不同位置所呈现的效果是不一样的，近处看可以看到清澈见底的湖水，远处看却是波光粼粼的湖面。现实生活中类似这种现象非常普遍，并且每天都可以观察到，当视线垂直于表面时，反射较弱，而当视线与表面呈一定夹角时，夹角越小，反射就越明显。而要研究夹角与反射光的关系时(同时折射也会伴随影响)，就需要了解菲涅尔效应。

原理

首先需要明确的是菲涅尔是一个人的名字，是他提出了用数学方式来描述我们在介绍部分描绘的现象，由于是他提出的数学方程，所以该方程又被称为菲涅尔方程(或称为菲涅尔条件)。菲涅尔方程的公式如下：

R(θ) = R(0)+(1- R(0))*(1-cos(θ))^5
R(0) = (n1 - n2)²/(n1 + n2)²

上面方程中的θ在有光照的情况下通常指的是光源方向(顶点到光源的向量)与摄像机方向(顶点到相机的向量)相加后所形成的半角向量与摄像机方向向量所形成的夹角，在不考虑光线影响的情况下，可把该半角向量用模型法线代替，即为摄像机方向向量与法线向量的夹角，R(0)表示0角度下的菲涅尔反射，n1是光源通常为空气或真空下的折射率，n2是表面材料的折射率，折射率根据材料的不同有所差异，如：真空的折射率为1.0，空气为1.000293，水为1.333333，钻石为2.417。大部分开发者在描述菲涅尔效应的着色效果编写中都会忽略折射率的影响，即n1 = n2，那么R(θ)就等于：
$$R(θ) = (1 - cos(θ))^5$$

这么做也是为了减少计算量，让菲涅尔方程的计算不至于太过复杂，但是有时候忽略折射率也会影响所呈现的效果，关于效果与计算量的取舍取决于开发者，这里不做过多讨论，R(θ)公式中的5次方在着色器编写中可作为可变量去做适当改变。前面在介绍部分我们说到菲涅尔效应是受视线与表面的夹角所影响，与表面的夹角越小，反射越强，把该结论用在该公式中，可以转换为：视线与法线的夹角越大反射越强。根据公式我们一起验证下该结论：

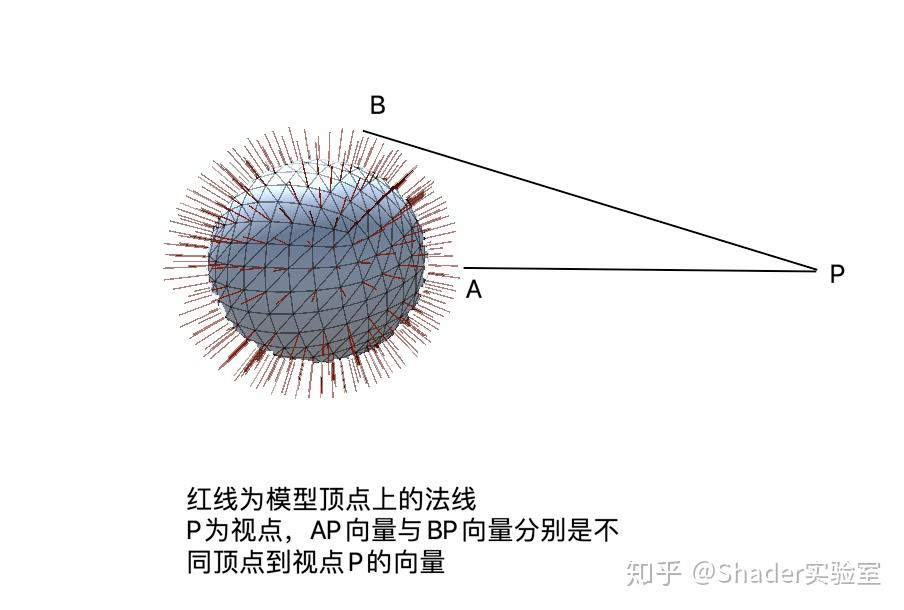
上图中，当点A到点B过渡时，视线与法线的夹角也将越来越大，假设AP与在该点A上的法线NA的夹角为0，BP与在该点B上的法线NB的夹角为120度(2π/3), 代入公式得：
$$R(0) = 0$$$$R(2π/3) = (1+0.5)^5 ≈ 7.6$$

论证结果确实证明了视线与法线的夹角越大反射越强的结论。

实验

着色器代码如下：

/*
** Simple example of rim lighting using fresnel reflection
*/

const int MAX_MARCHING_STEPS = 255;
const float MIN_DIST = 0.0;
const float MAX_DIST = 100.0;
const float PRECISION = 0.001;

float sdSphere(vec3 p, float r )
{
  vec3 offset = vec3(0, 0, -2);
  return length(p - offset) - r;
}

float sdScene(vec3 p) {
  return sdSphere(p, 1.);
}

float rayMarch(vec3 ro, vec3 rd) {
  float depth = MIN_DIST;

  for (int i = 0; i < MAX_MARCHING_STEPS; i++) {
    vec3 p = ro + depth * rd;
    float d = sdScene(p);
    depth += d;
    if (d < PRECISION || depth > MAX_DIST) break;
  }

  return depth;
}

vec3 calcNormal(vec3 p) {
    vec2 e = vec2(1.0, -1.0) * 0.0005;
    return normalize(
      e.xyy * sdScene(p + e.xyy) +
      e.yyx * sdScene(p + e.yyx) +
      e.yxy * sdScene(p + e.yxy) +
      e.xxx * sdScene(p + e.xxx));
}

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
  vec2 uv = (fragCoord-.5*iResolution.xy)/iResolution.y;
  vec3 col = vec3(0.1);

  vec3 ro = vec3(0, 0, 3);
  vec3 rd = normalize(vec3(uv, -1));

  float d = rayMarch(ro, rd);

  vec3 p = ro + rd * d;
  vec3 normal = calcNormal(p);
  vec3 lightPosition = vec3(4, 4, 7);
  vec3 lightDirection = normalize(lightPosition - p);

  float diffuse = clamp(dot(normal, lightDirection), 0., 1.);
  vec3 diffuseColor = vec3(0, 0.6, 1);

  float exponent = 2.; // lower number makes lighting go deeper into sphere
  float fresnel = pow(clamp(1. - dot(normal, -rd), 0., 1.), exponent);
  vec3 rimColor = vec3(1, 0.5, 1);
  
  vec3 sphereColor = diffuse * diffuseColor + fresnel * rimColor;
  
  col = mix(col, sphereColor, step(d - MAX_DIST, 0.));

  fragColor = vec4(col, 1.0);
}

菲涅尔效应原理与实现

介绍

实验

0 Answers