在计算机图形应用程序中,四元数用于表示三维旋转。与使用欧拉角定义通用旋转变换的传统方法相比,四元数提供了一些关键优势,比如四元数可以在给定的两个方向之间进行插值;因此对于需要方向插值的关键帧动画使用四元数的方式会非常方便。
本篇概述了四元数的代数、四元数变换的几何解释以及基于四元数的线性和球面插值函数。介绍了使用欧拉角、angle-axis(角度轴)表示和四元数的旋转插值方法的比较。
Complex Numbers
四元数是秩为4的超复数,因此回顾一下与复数相关的一些基本概念,以更好地了解四元数操作是有必要的。复数通常以z = a+bi 的方式表示,其中i是虚数,并且 i² = -1,那么虚数是什么?其实虚数的来源是为了解决特定无解的方程,比如:
$$
x^2+1=0
$$
分解得出x² = -1,这显然无解,因为任何实数的平方都为正数,但是对于数学家来讲,没有无解的方程,所以虚数因此诞生,即:
$$
i^2=−1
$$
这个等式是否有意义我们不作深究,只需要知道它是一种数学表示就好。
我们可以通过下述等式表述复数:
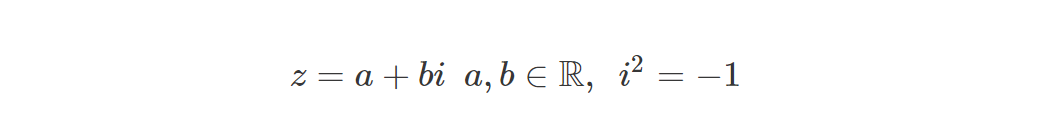
其中 a、b 分别表示 z 的实部和虚部,因此对复数z可以使用two-tuple(二元组) 符号 (a, b)表示。
可以认为所有实数都是b=0的复数、所有虚数都是a=0的复数。
Adding and Subtracting Complex Numbers
复数可以分别通过加减实数和虚数部分来作加减运算:
复数加法:
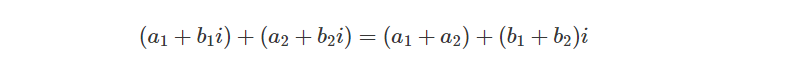
复数减法:
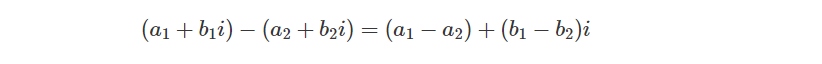
Multiply a Complex Number by a Scalar
复数与标量相乘是通过将复数的实部与虚部分别乘以标量来作乘法运算:
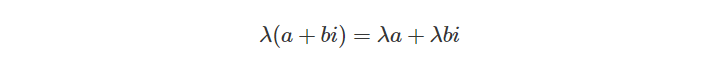
Product of Complex Numbers
两个复数的乘法可以通过应用普通代数规则相乘:
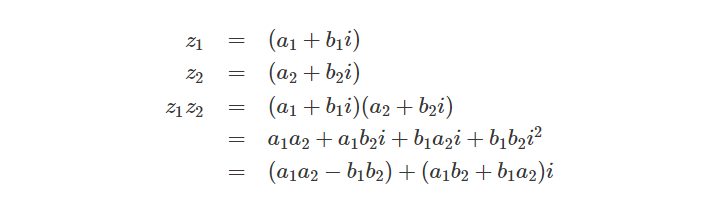
Square of Complex Numbers
复数也可以通过与自身相乘求取平方值:
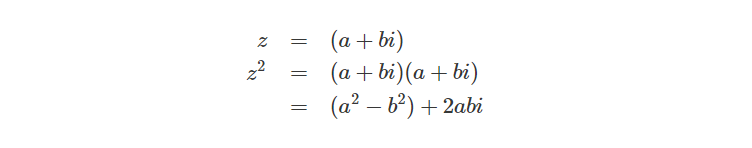
Complex Conjugate
两个实部相等,虚部互为相反数的复数互为共轭复数(conjugate complex number)。当虚部不为零时,共轭复数就是实部相等,虚部相反,如果虚部为零,其共轭复数就是自身(当虚部不等于0时也叫共轭虚数)。复数z的共轭复数记作z(上加一横),有时也可表示为Z 。
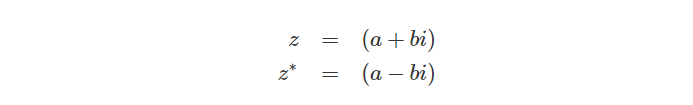
复数与它的共轭复数相乘会得到特殊的结果:
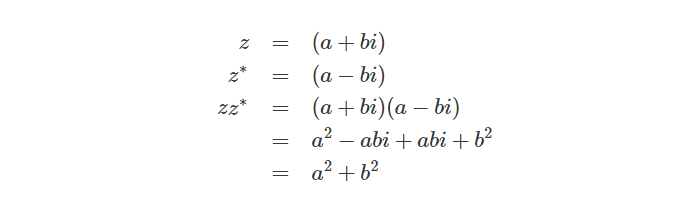
Absolute Value of a Complex Number
我们可以用复数的共轭来计算复数的绝对值(或模)。复数的绝对值是复数乘以它的共轭复数的平方根,记为|z|:
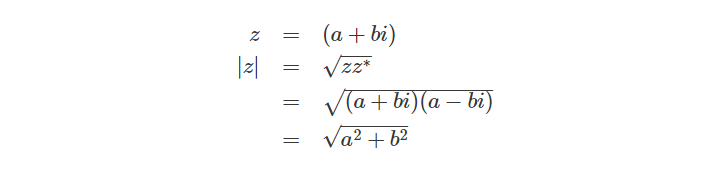
Quotient of Two Complex Numbers
要计算两个复数的除法运算,我们需要将分子和分母同时乘以分母的共轭复数,目的是为了让分母实数化,以便更容易计算结果:
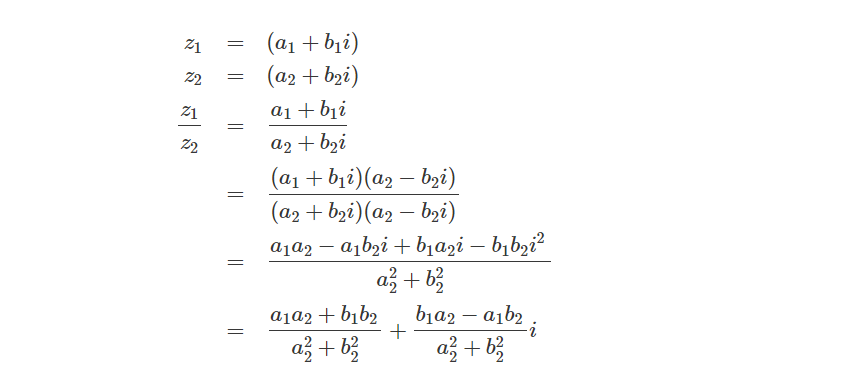
Powers of i
既然我们已经知道了 i² = -1,那么对i进行其它次幂的运算同样可以知道结果:
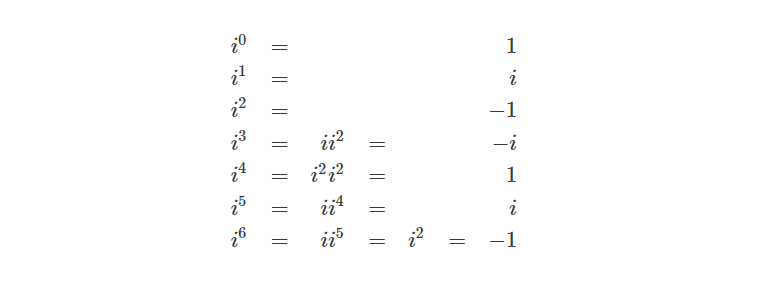
如果我们继续扩展上式对i进行无限次幂的运算,其结果总会得到下述规律:
$$
(1, i,−1,−i, 1, i, -1, -i, 1…)
$$
同样的,类似的情况也会出现在对i进行负次幂的运算,先看实数的负次幂:
所以i的负次幂可得:
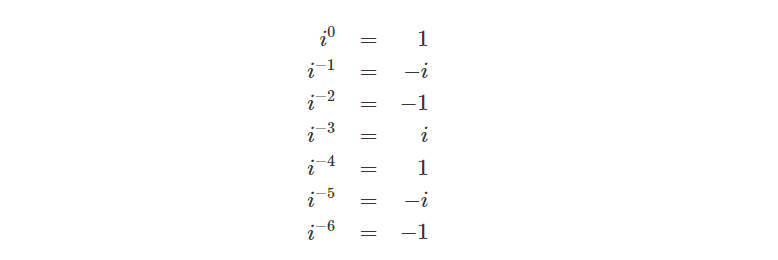
对上面的规律有没有似曾相识?我们在笛卡尔坐标系中见过类似的规律,但形式是(x, y,−x,−y, x,…),它是通过在二维笛卡尔平面上逆时针把一个点旋转90°生成的,而另一种序列形式(x,−y,−x, y, x,…)是通过在二维笛卡尔平面上顺时针对一个点旋转90°生成的。
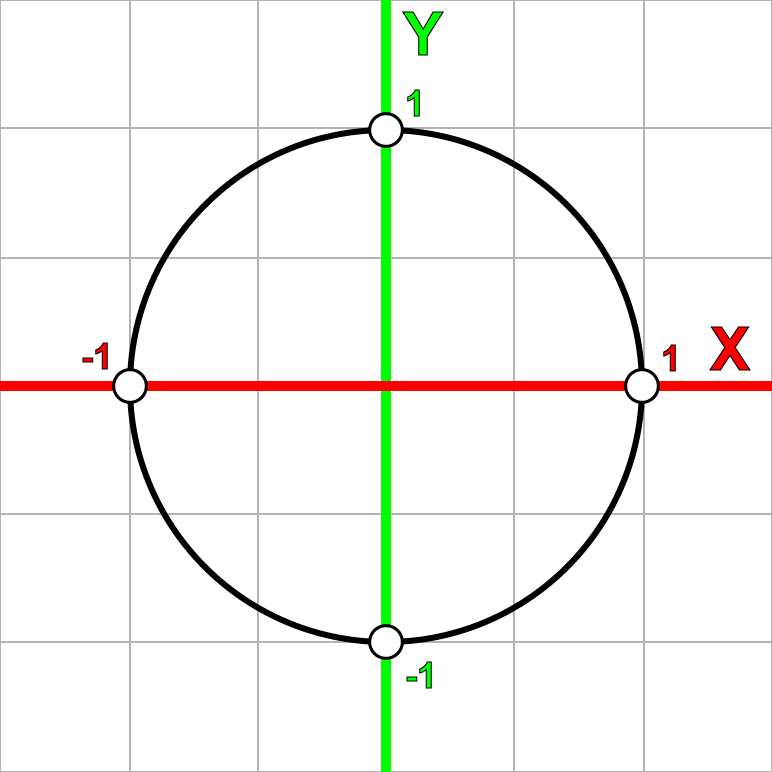
The Complex Plane
我们可以根据笛卡尔坐标系的方式将复数映射到一个称为复平面的二维坐标系中,方法是将实数部分映射到横轴上,将虚数部分映射到纵轴上。
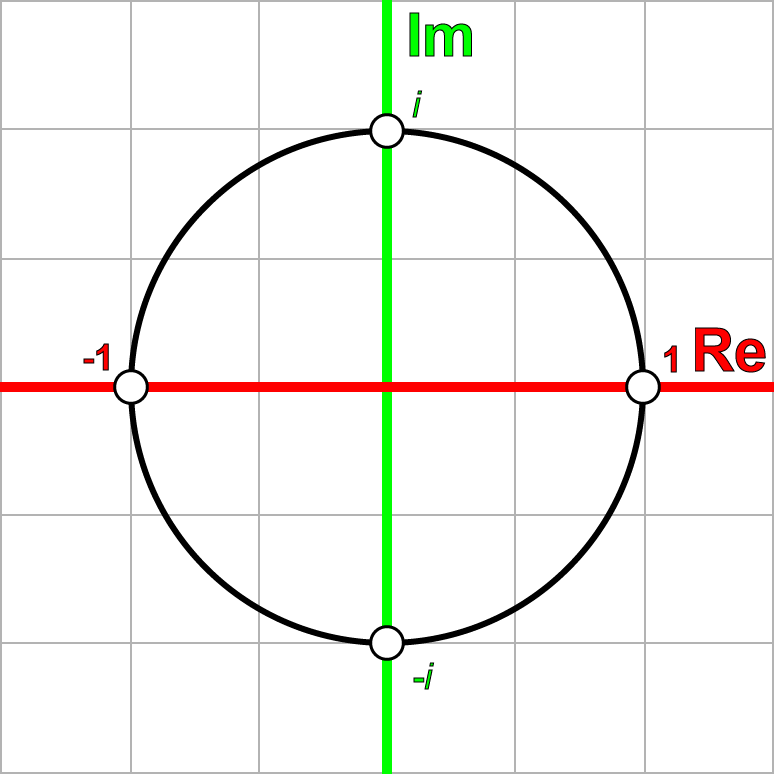
根据前面的规律,我们可以发现,如果我们将一个复数乘以i,它可以在复平面上以90°的增量进行旋转。
为了证明上述推断,我们可以在复平面上取任意点p:
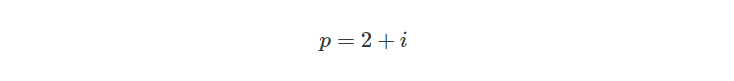
然后让p乘上i,可得q:
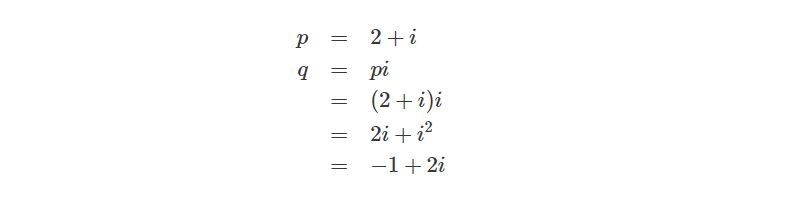
让q乘上i,可得r:
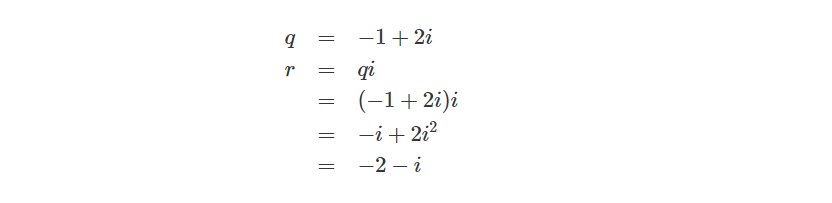
再让r乘上i,得到s:
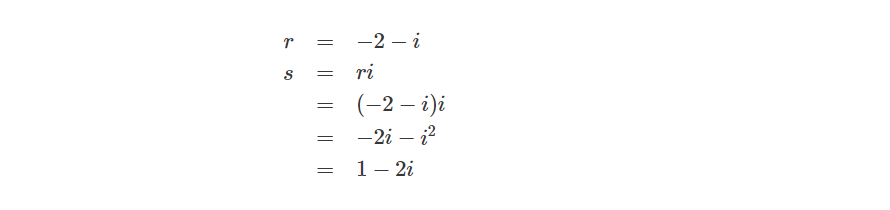
最后让s乘上i,得到t:
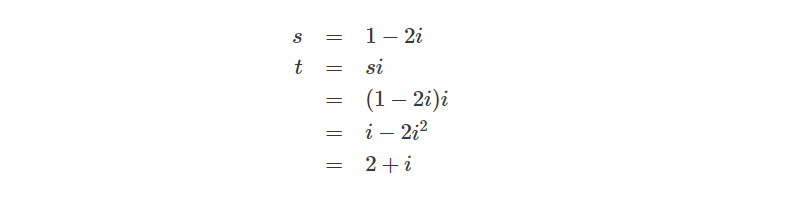
可以知道最后的结果t与p相等,上述变换过程可以通过下图描述:
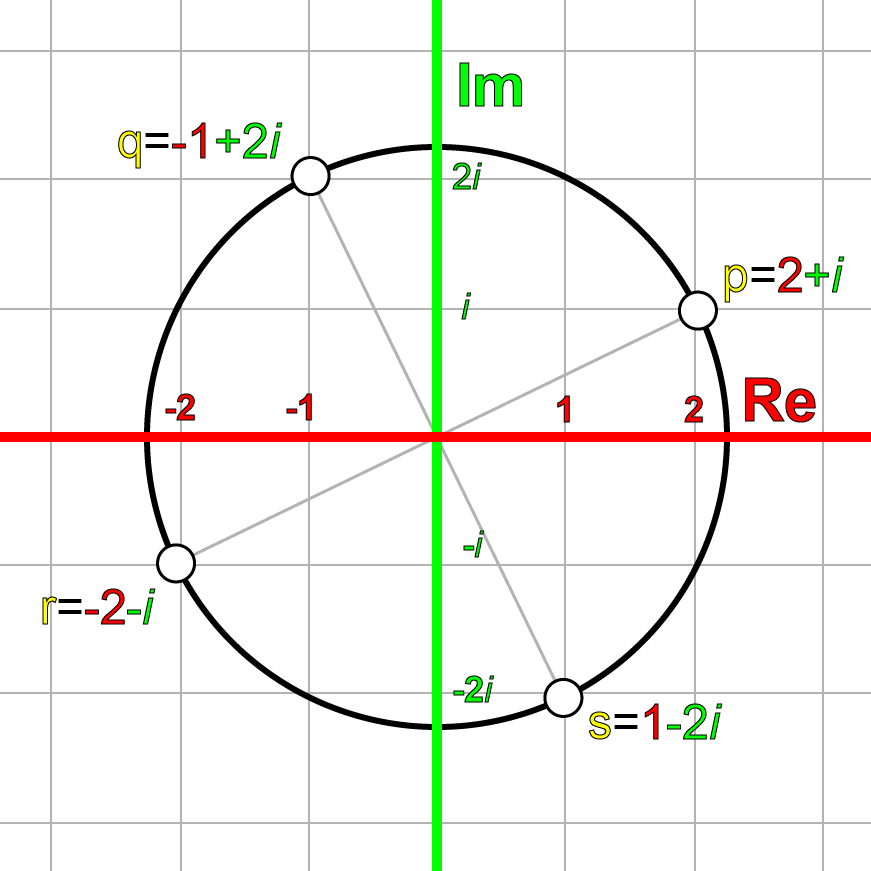
我们也可以在复平面上进行顺时针旋转,它是将复数乘以−i完成。
Rotors
上面我们通过乘上i或-i对坐标点在复平面上以90°为单位进行的旋转变换,下面我们需要求取任意角度的旋转,我们定义了复数q:
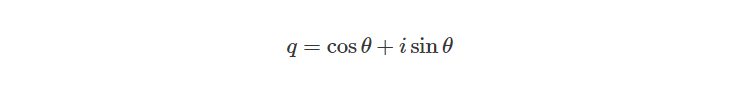
接着我们让任意复数乘以复数q进行任意角度的旋转变换:
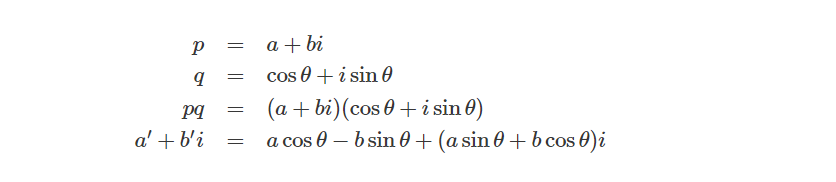
根据上面结果,我们可以写成矩阵形式:
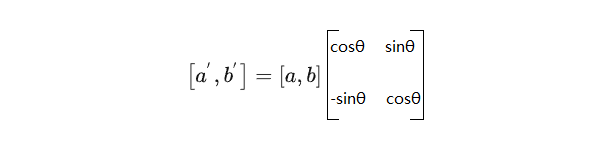
回顾旋转矩阵推导的过程:
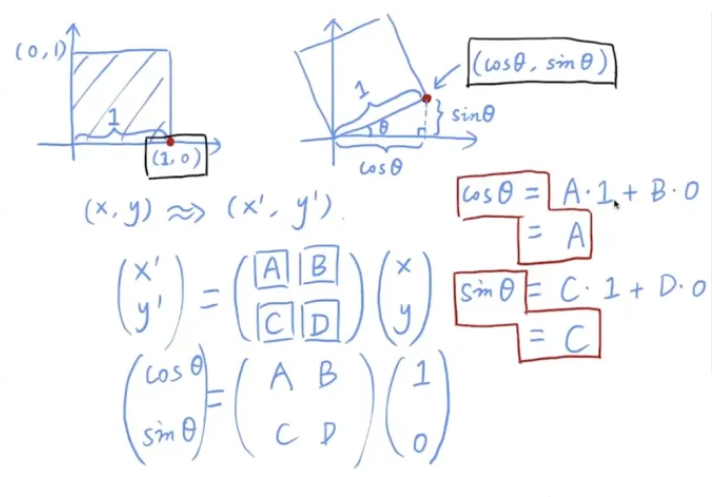
可知,旋转矩阵是对单位向量(1, 0)和(0, 1)两坐标轴所形成的坐标系进行的旋转操作:
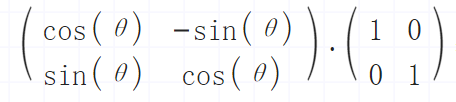
上述矩阵的乘法可以理解为是对以单位向量(1, 0), (0, 1)两坐标轴形成的坐标系旋转θ角度的操作,其中(1, 0),(0, 1)两坐标轴互相垂直。映射为上述复平面的公式就可以理解为是对以(1, 0i), (0, 1i)两坐标轴形成的坐标系旋转θ角度的操作。
所以它是绕原点逆时针旋转复平面上任意点的方法。
Quaternions
有了复数系统和复平面的储备,我们可以将其扩展到三维空间,在三维空间中我们使用四元数表示,除了虚数i之外,在四元数中额外加入了两个虚数,它的一般形式为:
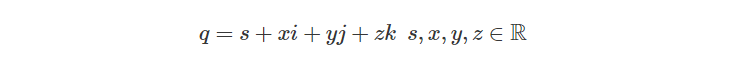
其中:
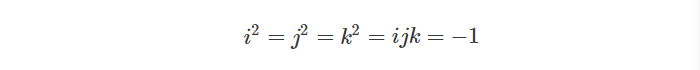
并且:
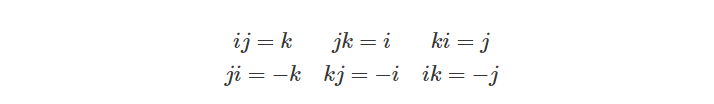
我们可以注意到i,j和k之间的关系非常类似于单位笛卡尔坐标轴向量的叉乘规则:
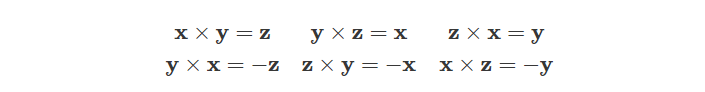
同时三个虚数i、j和k可以分别用来表示三个笛卡尔坐标轴的单位向量,它们具有与虚数相同的性质,如 i² = j² = k² = −1。
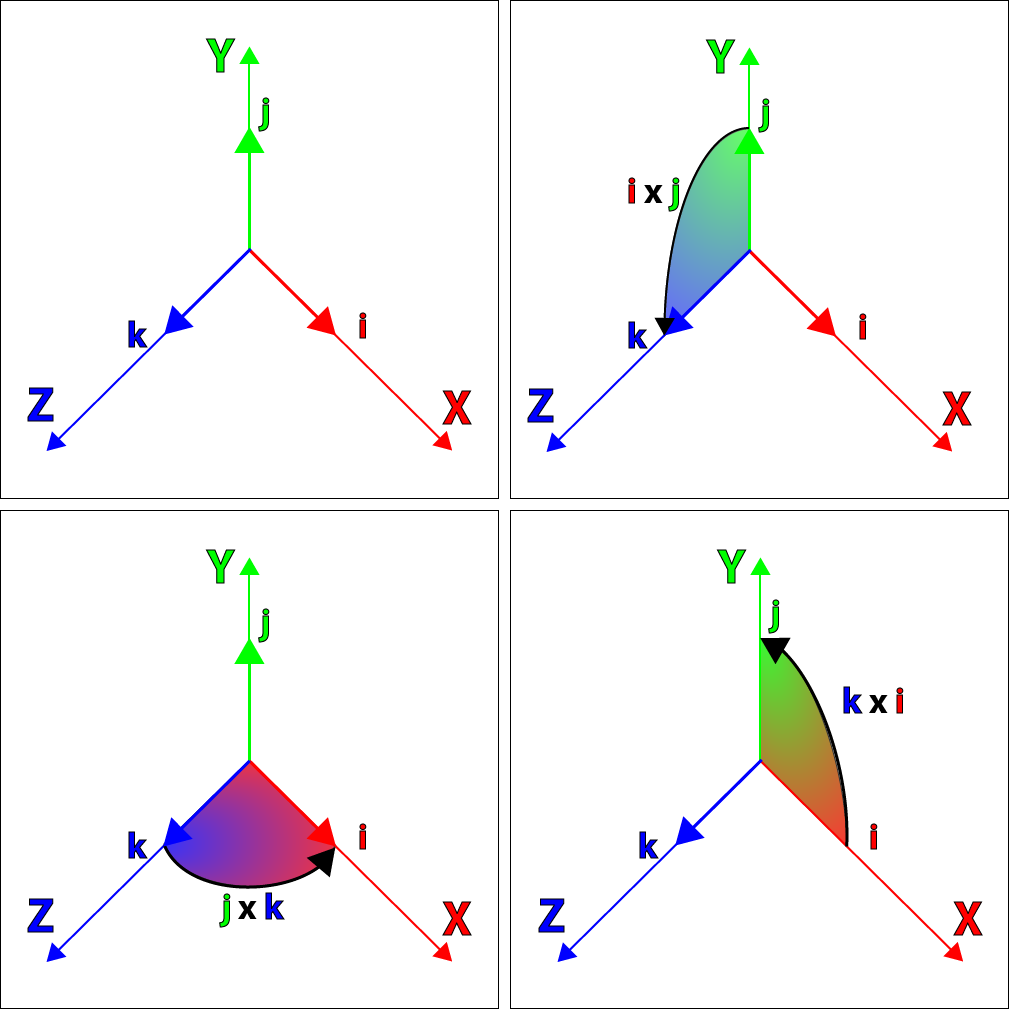
上图显示了由i、j和k组成的笛卡尔单位坐标轴向量之间的关系。
Quaternions as an Ordered Pair
我们也可以将四元数表示为有序数对:
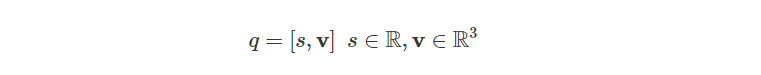
其中 v 也可以用它的各个分量来表示:
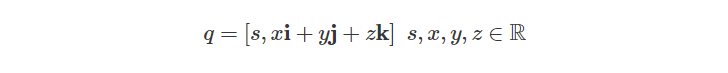
使用这种表示法,我们可以更容易地看出四元数和复数之间相似的地方。
Adding and Subtracting Quaternions
四元数可以像复数一样做加减运算:
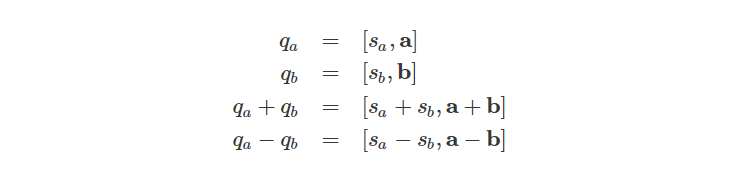
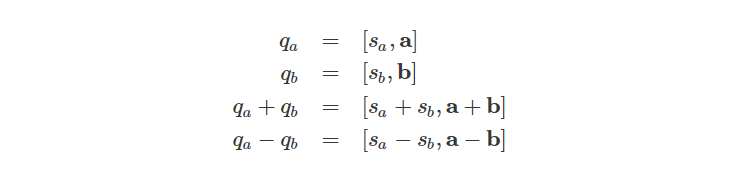
Quaternion Products
我们也可以计算两个四元数的乘积:
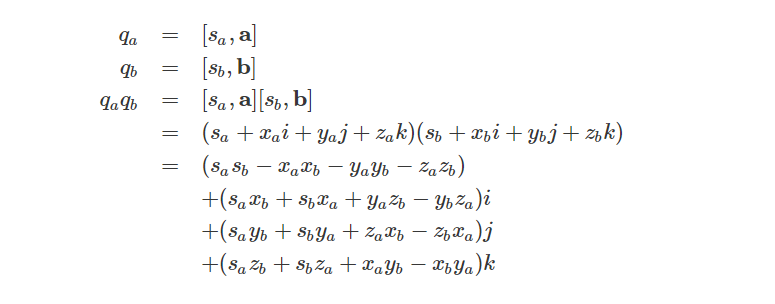
相乘的结果可以得到另一个四元数。如果我们将上面表达式中的虚数i、j和k替换为有序对:
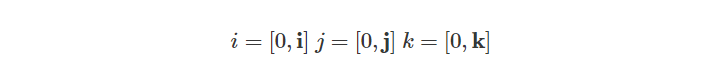
而 (SaSb - XaXb - YaYb - ZaZb)部分可以看成乘上系数1,而系数1可以看成有序对[1, 0],代入可得:
将所得结果用有序对的和来表示:
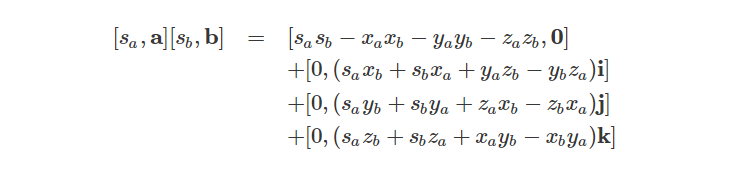
展开后得到:
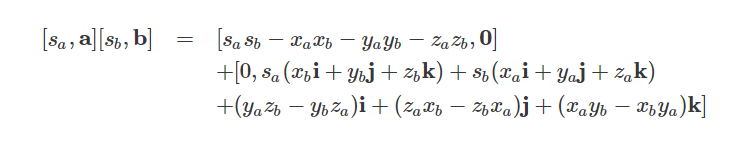
上述求解结果可以看到它是由两个有序对(四元数)构成。第一个有序对是实四元数(相当于复数的实数),第二个有序对是纯四元数(相当于复数的纯虚数)。这两个有序对可以组合为一个新的有序对:
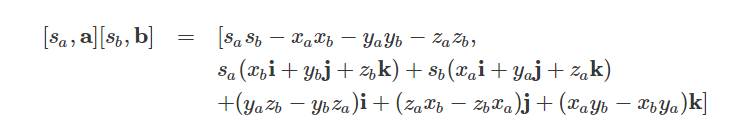
我们可以把a与b的实际值代入到上式:
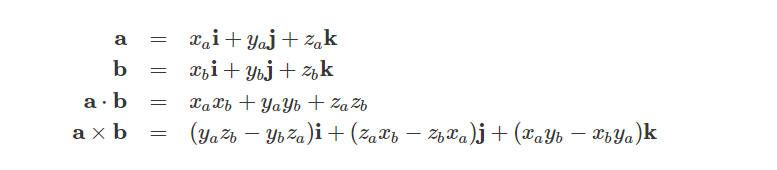
最后我们得到:
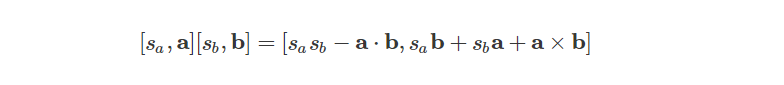
这是四元数乘积一般式。
A Real Quaternion
实四元数是向量项为0的四元数:
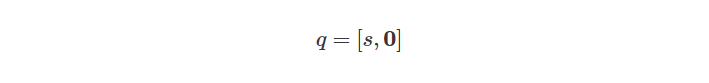
两个实四元数的乘积是另一个实四元数:
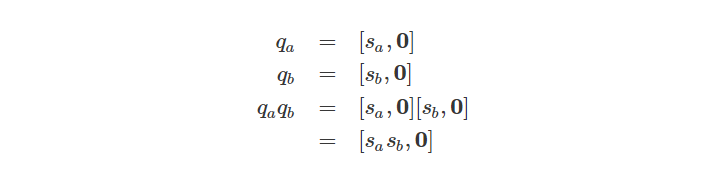
这类似于两个包含零虚数项的复数的乘积。
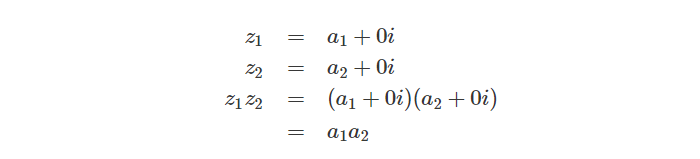
Multiplying a Quaternion by a Scalar
我们还可以用四元数与一个标量相乘:
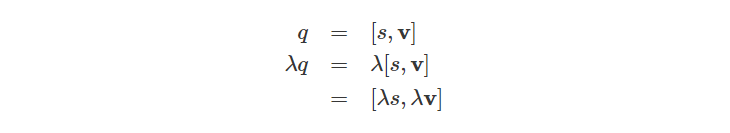
为了验证这个结果成立,我们可以通过使用上面四元数乘积的方式来验证结果,将一个四元数与另一个实四元数相乘:
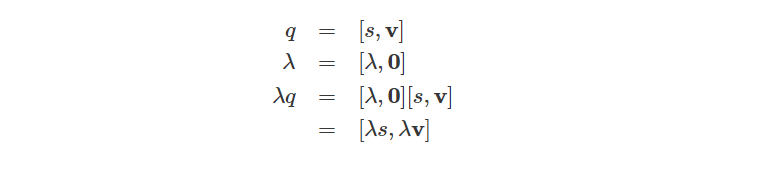
Pure Quaternions
与实四元数类似,也将纯四元数定义为具有零标量项的四元数:
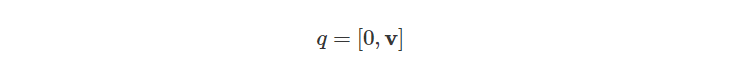
或者用实际的组成部分来描述:
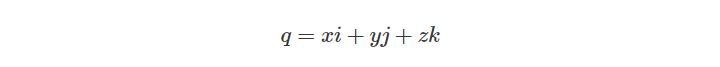
我们还可以计算两个纯四元数的乘积:
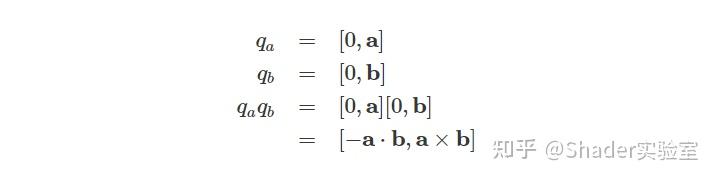
这是根据四元数一般式得到的。
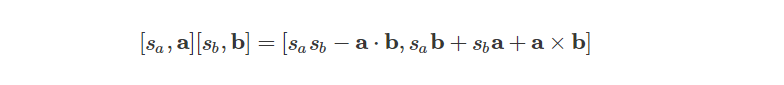
Additive Form of a Quaternion
上面求取一般式的时候已经接触到我们可以将四元数表示为实四元数和纯四元数的加法操作:
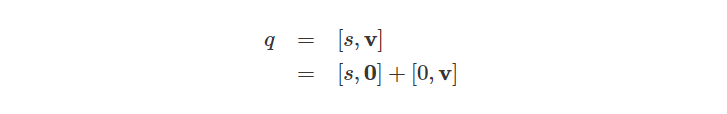
Unit Quaternion
给定一个任意向量v,我们可以把这个向量描述为向量的长度和该向量的单位向量的乘积:
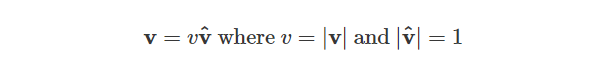
将这个定义与纯四元数的定义结合起来,得到:
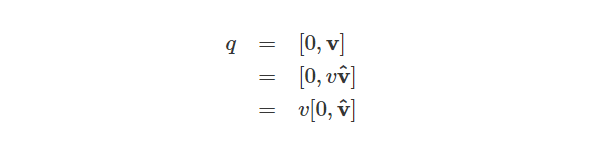
所以我们也可以这样描述一个单位四元数,它有一个标量为0和一个单位向量:
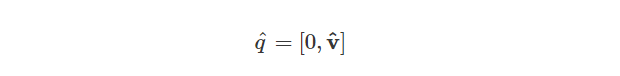
Binary Form of a Quaternion
现在,我们可以将单位四元数的定义和四元数的加法形式结合起来,就可以创建一个新的四元数表示形式,它类似于复数的表述方式:
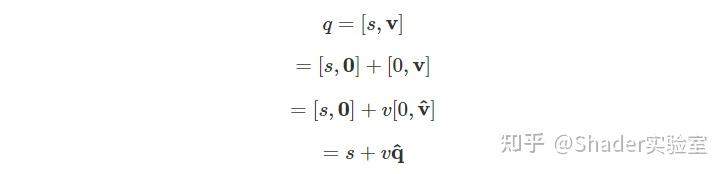
这样它与复数的表述形式就一致了:
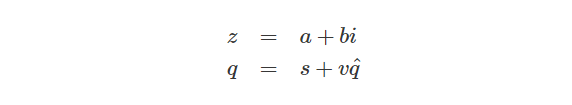
Quaternion Conjugate
共轭四元数可以通过对四元数的向量部分求反来计算:
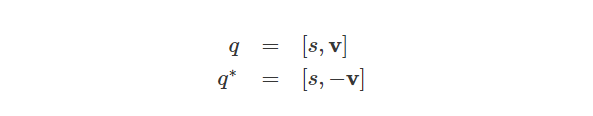
四元数与其共轭四元数的乘积为:
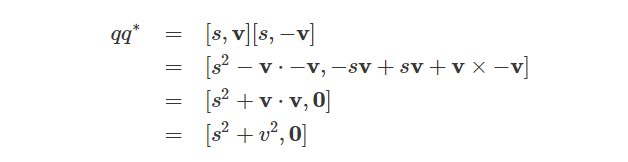
Quaternion Norm
回顾下如何求取复数的模以及复数与共轭复数相乘的结果:
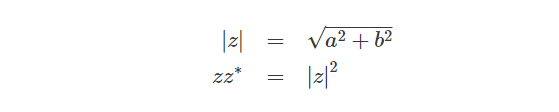
类似地,四元数的模求取方式为:
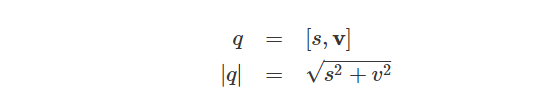
所以四元数与其共轭四元数相乘的结果为:
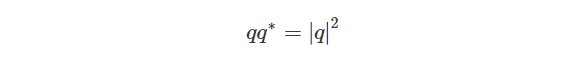
Quaternion Normalization
四元数是通过除以四元数的模长 |q| 进行归一化:
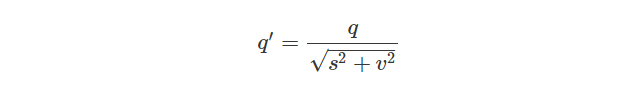
比如我们定义一个四元数q:
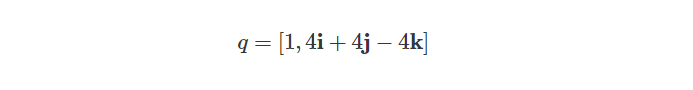
首先,我们必须计算四元数的模长:
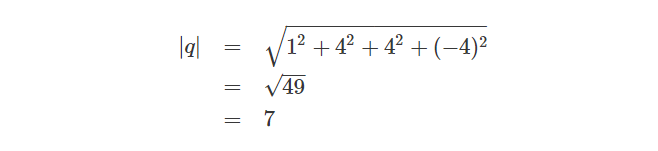
然后,我们用四元数除以它自身的模长来计算归一化四元数:
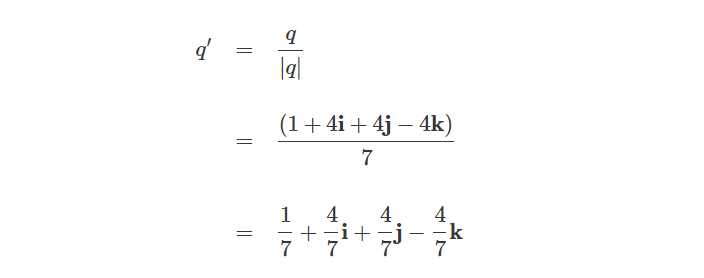
Quaternion Inverse
四元数的逆记为q^-1(q的负一次方)。为了计算四元数的逆,我们取四元数的共轭并除以它模长的平方:
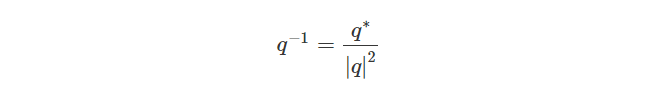
为了验证上式成立,我们可以用四元数与其四元数的逆相乘:
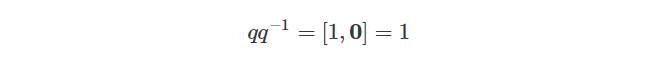
再把上式的左右两边同时乘以四元数的共轭得到:
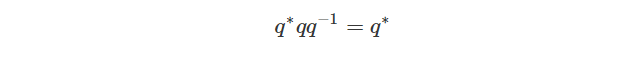
通过代换等式可以得到:
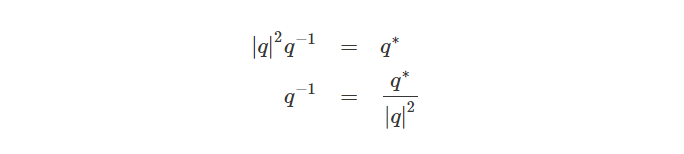
对于模长为1的单位四元数,我们可以写成:
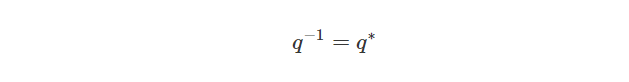
Quaternion Dot Product
类似于两个向量的点积,我们也可以通过将相应的标量部分相乘并将结果相加来计算两个四元数之间的点积:
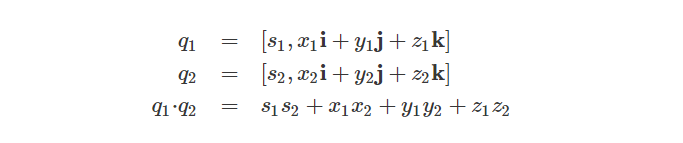
我们还可以使用两个四元数的点积来计算它们之间的夹角:
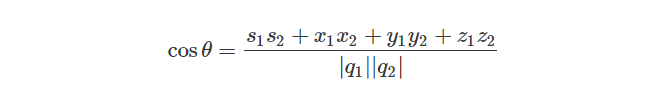
对于单位四元数我们可以简化计算过程:
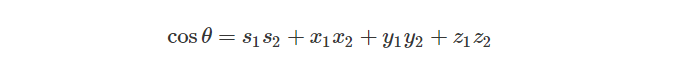
Rotations
复数相关内容介绍中我们知道在复平面上我们通过定义下述公式来旋转复平面上的点:
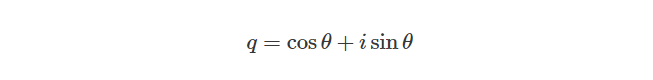
然后再根据四元数与复数的相似性,我们可以定义一个四元数,同样也可以用于在3d空间中旋转一个点:
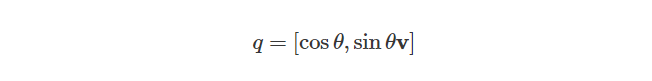
为了验证这个结论的合理性,我们通过计算四元数q和向量p的乘积来验证这个理论是否成立。首先,我们可以将向量p表示为纯四元数,形式如下:
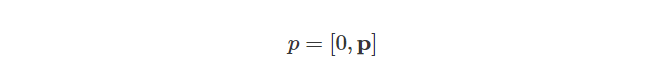
而四元数q的形式如下:
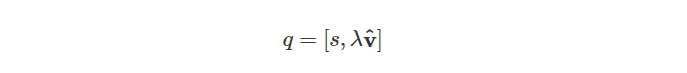
然后可得转换后的向量p':
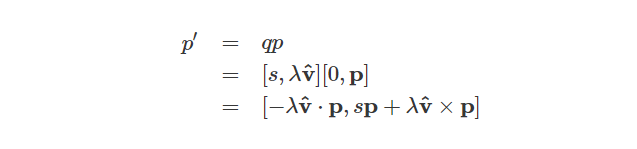
可以看到,结果是一个具有标量以及向量部分的普通四元数。
让我们首先考虑向量p垂直于单位向量v的“特殊”情形,在这种情况下,点积项−λv⋅p=0,结果就变成了纯四元数:
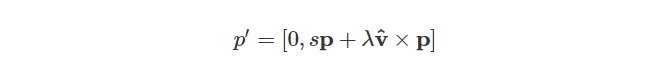
在这种情况下,要让向量p围绕单位向量v旋转,我们只需代入s=cosθ 和 λ=sinθ,可得:
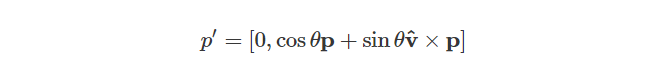
例如,让我们围绕z轴旋转向量 p 到45°角,那么我们的四元数q就变为:
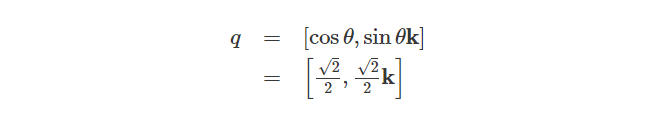
我们可以取一个向量p,它满足p垂直于向量k(四元数空间中的k轴):
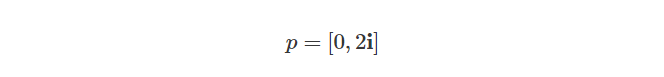
现在我们可以求取q与p的乘积:
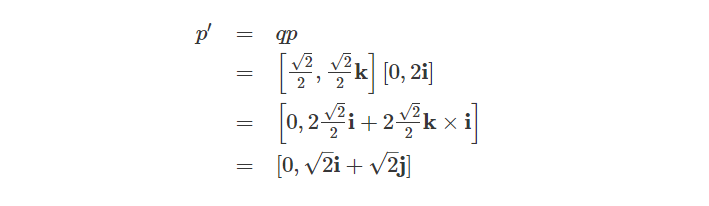
这就得到了一个围绕k轴旋转45°的纯四元数。我们还可以验证它的结果向量的模长是不变的:
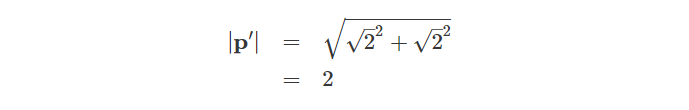
这正是我们所期望的结果!
我们可以用下图进行可视化:
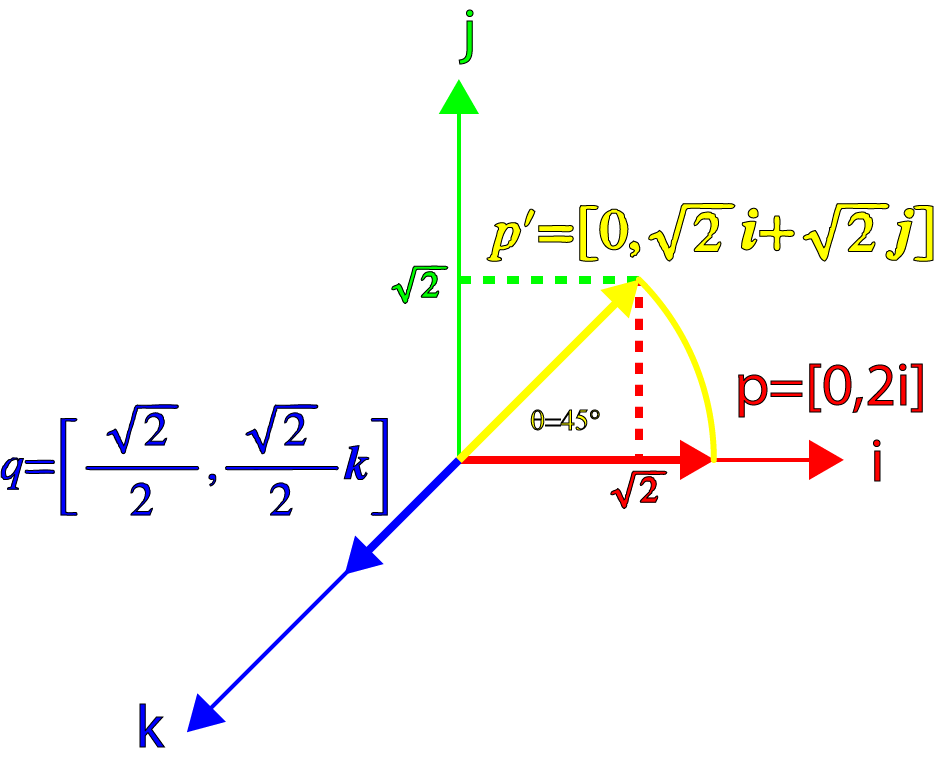
上面我们考虑的是向量p与四元数垂直(正交)的情况,现在让我们重新考虑与p没有互相垂直(正交)的情形。如果我们重新定义四元数的向量部分,它可以让向量p旋转45°,我们得到:
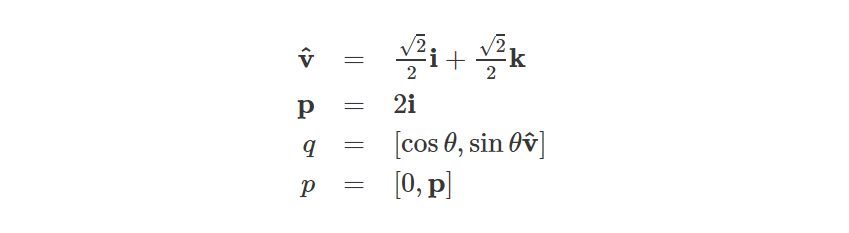
用向量p乘以四元数q,得到:
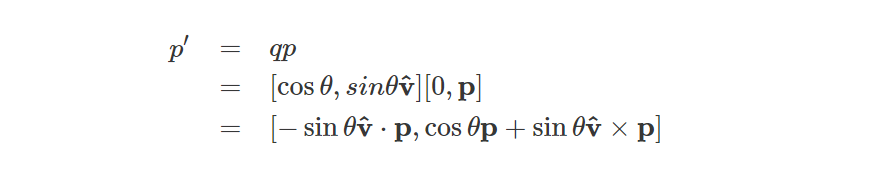
代入单位向量v和p以及θ = 45°,我们得到:
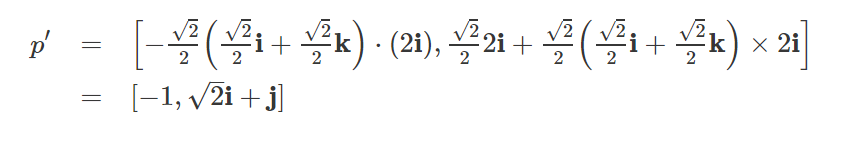
它的结果不再是纯四元数,并且,也没有旋转45°角,而且向量部分的模长也不再等于2(反而变小了,成了根号3)。
旋转的可视化过程如下:
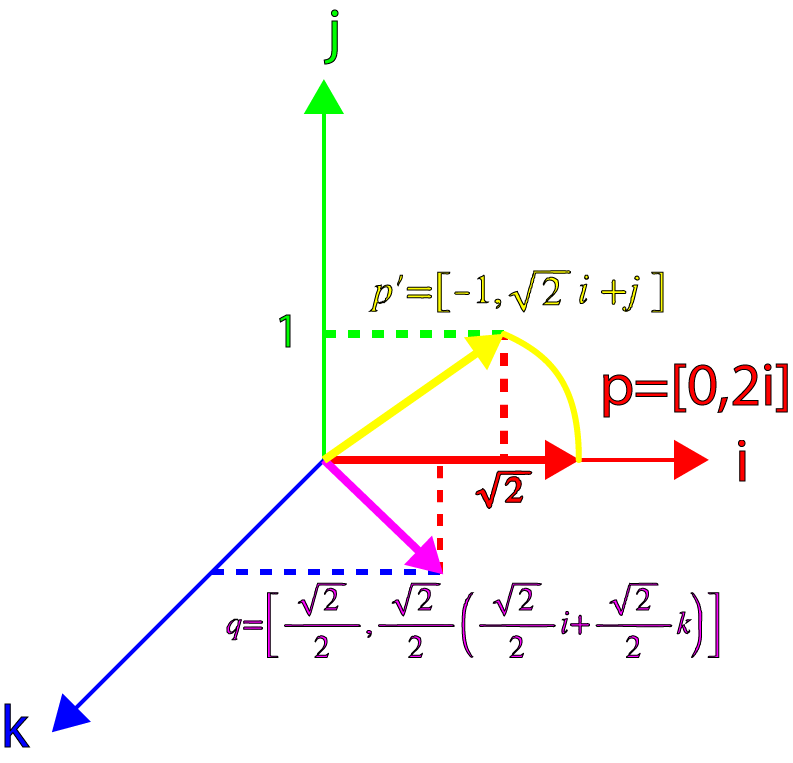
严格意义上讲,在3D空间中表示四元数p'是不正确的,因为四元数实际上是一个4维空间。这里为了简单起见,只对四元数的向量的分量部分进行可视化。
然而,这并不是说我们没法对一个向量进行旋转操作了。如果我们用qp的结果乘以q的逆,那么结果是一个纯四元数,并且向量分量的模长部分会保持不变(即λ,p = [s, λv])。我们看看能不能把这个应用到我们的例子中。
首先,让我们计算$q^-1$:
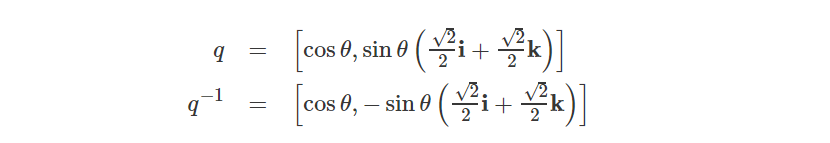
可以看到$q^-1$与q*(q的共轭)相等,这是因为q的模长等于1:
$$
|q| = cosθ²+\frac{2sinθ²}{4}+\frac{2sinθ²}{4} = 1
$$
此时$q^-1$等于q*。
代入θ等于45°,可得:
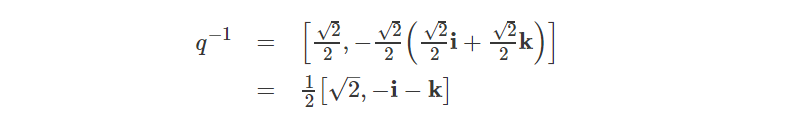
将qp与q-1相乘得到:
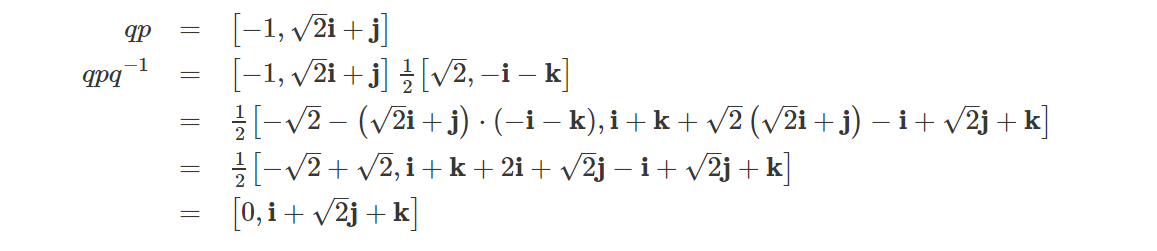
最后它又等于一个纯四元数了,结果是:
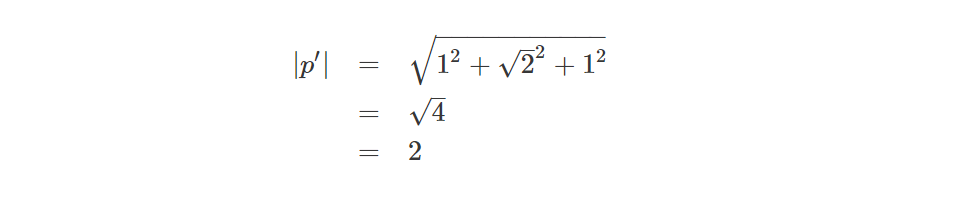
现在我们已经能确保旋转后的p向量与旋转前的模长是一致的。
下图是旋转的可视化结果。
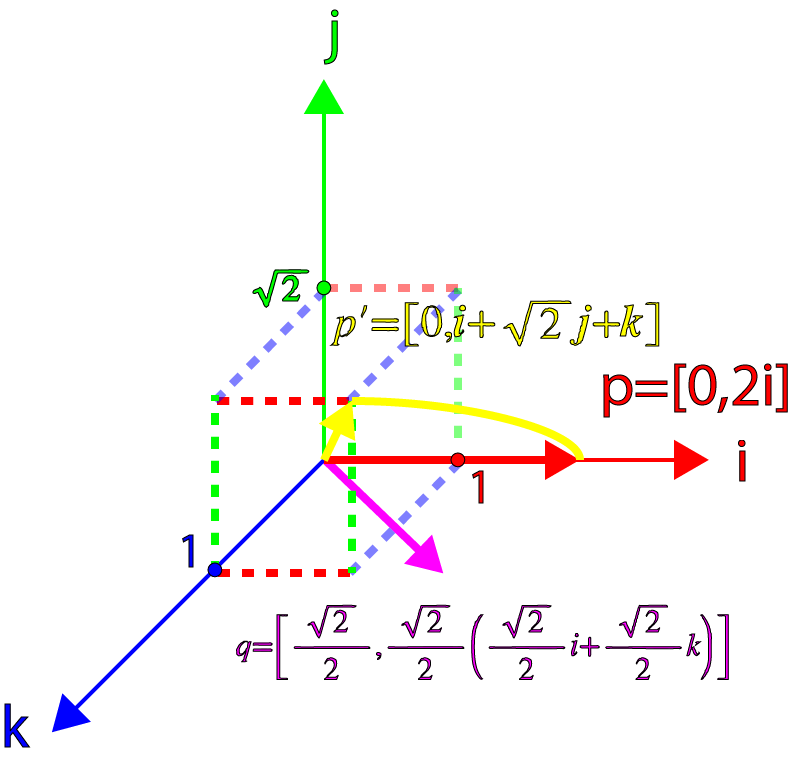
到这里,我们可以看到所得的结果是一个纯四元数,并且旋转后的向量的模长能够保持不变,但发现向量已经被旋转轴旋转了90°,而不是45°,这是我们期望的结果的两倍。因此,为了正确地将向量p围绕任意轴v旋转一个角度θ,我们必须将旋转角度考虑为半角,并对四元数构造成如下形式:
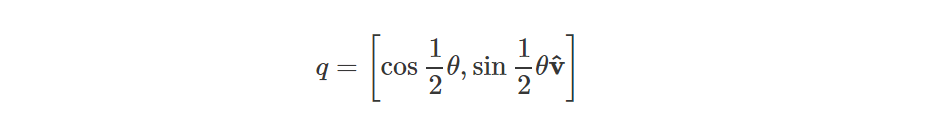
上式是旋转四元数的一般方程。
Quaternion Interpolation
在计算机图形学中使用四元数的一个最重要的原因是四元数非常擅长用于描述空间中的旋转。四元数解决了在3D空间中旋转点的一些问题,例如当我们用欧拉角表示旋转时,万向锁就是其中要面对的一个问题。
使用四元数,我们可以定义几种方法来描述三维空间中的旋转插值。我们讨论的第一个方法称为SLERP,用于在两个方向之间平滑地过渡某个点。第二种方法是SLERP的扩展,称为SQAD,它通过定义路径的方向序列来进行插值。
SLERP
SLERP代表球面线性插值。它提供了在两个方向之间平滑插值点的方法。
我们使用q1表示方向一,用q2表示方向二,要被插值的点用p表示,插值后的点用p'表示。插值参数t将从q1 (t=0)到q2 (t=1)对p进行平滑插值。
首先看下标准线性插值公式:
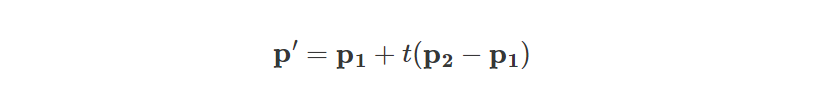
应用标准线性插值公式的一般步骤为:
1.计算p2与p1之间的差。
2.根据1的结果,乘上参数t(0 <= t <= 1),得到原始点p的增量。
3.把2中的增量与原始点p1相加,得到的值p'就是插值后的结果。
我们可以使用相同的原理在两个四元数代表的不同方向之间进行插值。
QUATERNION DIFFERENCE
我们按照标准线性插值公式的第一步要求,首先计算q1和q2之间的差值。对于四元数,这相当于计算两个四元数之间的角度差。
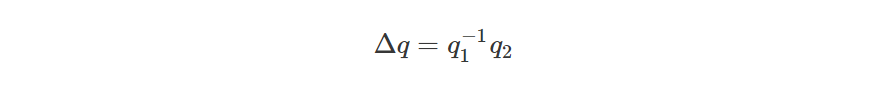
等式的推导可以通过:
$$
q2 = q1\Delta q
$$
所以:
$$
\Delta q = q1^{-1}q2
$$
QUATERNION EXPONENTIATION
下一步我们需要计算增量了,我们可以通过将t限定在[0~1]的范围内,并对四元数的t次方进行运算(这里的四元数的值指的是通过第一步过程求取的结果)。
要求取四元数的幂运算,一般通过如下公式:
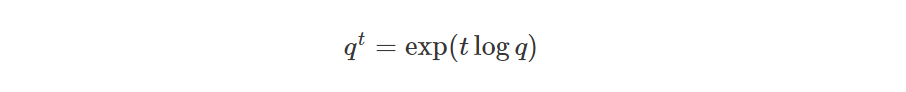
四元数的指数函数由下式得到:
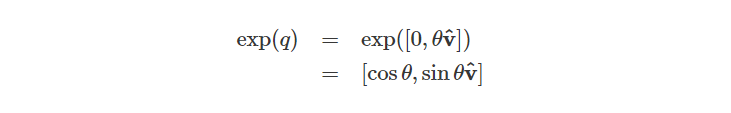
四元数的对数函数由下式得到:
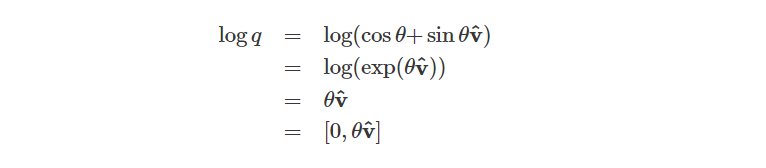
当t= 0时,我们得到:
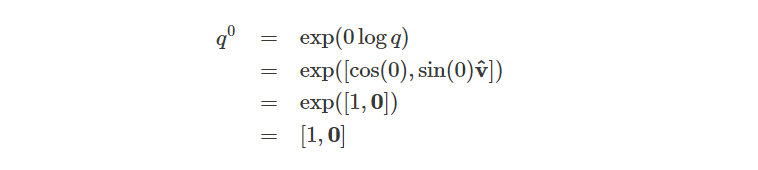
当t等于1时,我们得到:
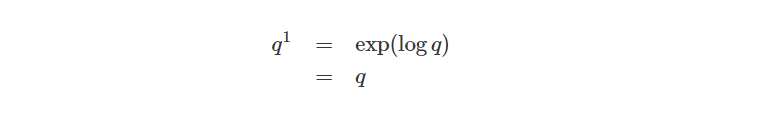
FRACTIONAL DIFFERENCE OF QUATERNIONS
最后,我们通过上一步计算后的增量值与初始四元数q1相乘,得到的结果就是插值后的四元数q':
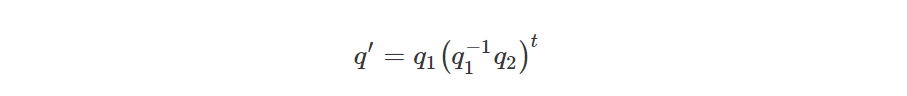
这是运用四元数球面线性插值的一般式。但是这并不是我们实践中经常用到的求取 SLERP 结果的通用方式。
我们介绍另一种方法,该方法可以把向量的球面插值应用到四元数的球面插值中。向量的球面插值的一般式定义如下:
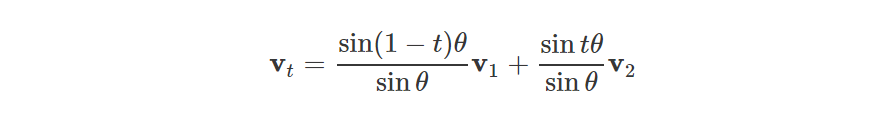
可用下图可视化表示:
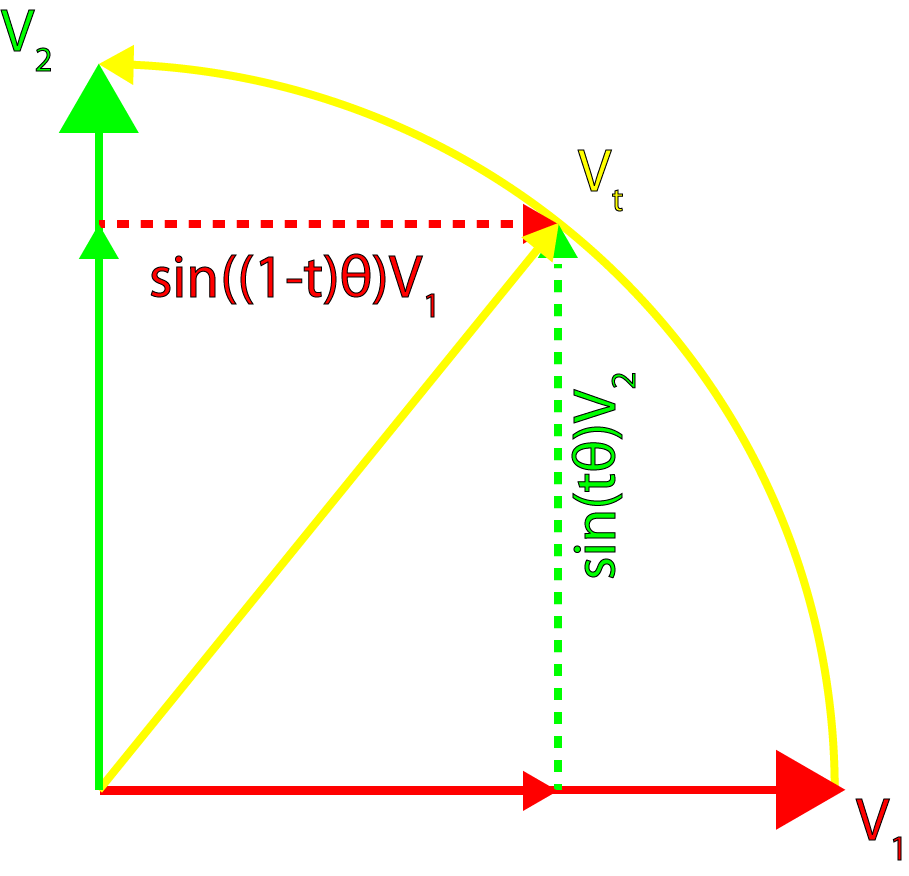
这个公式可以不加修改地应用于四元数中:
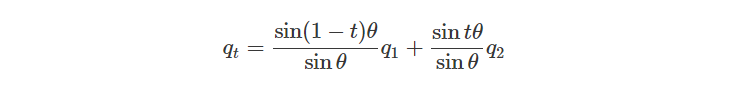
角度θ的计算可以通过q1和q2的点积计算得到:
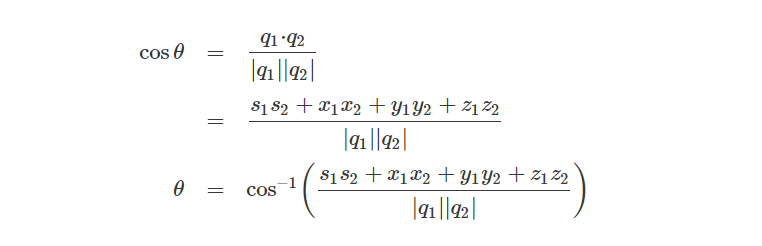
CONSIDERATIONS
在应用上述公式的过程中,有两个问题必须加以考虑。
首先,如果四元数点积的结果是负值,那么所得到的实时插值结果将围绕4D球体的表面进行“更长距离”的移动,这并不一定是我们想要的。为了解决这个问题,我们可以先计算点积的结果,如果它是负的,那么我们可以对其中一个四元数的方向向量取反。对四元数的标量和向量部分取反并不会改变它所代表的方向,但通过这样做,我们可以保证旋转过程经过的"路径"将是最短的。
另一个问题是当两个四元数q1和q2之间形成的角度θ很小时,那么sinθ由于精度等各种原因就有可能变为0。如果这种情况存在,那么当我们除以sinθ 时,我们将得到一个未定义的结果。此时,我们只能通过使用两个四元数线性插值的方式来求取(即第一种方式)。
SQUAD
正如SLERP可用于计算两个四元数之间的插值一样,SQUAD(Spherical and Quadrangle)可用于在旋转路径上进行平滑插值。
假设我们有一个四元数序列:
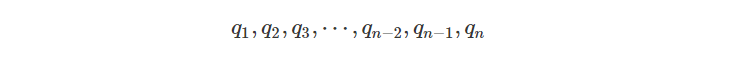
还定义了可作为中间控制点的“辅助”四元数(si):
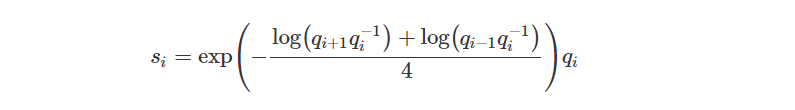
接着,沿着子曲线的方向就可以定义为:
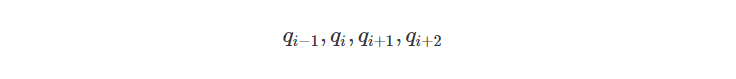
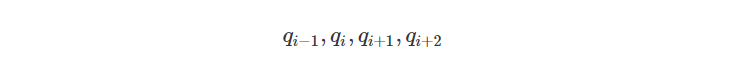
那么此时在t时间点SQUAD的插值结果为:
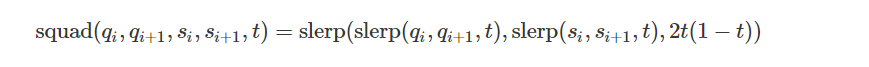
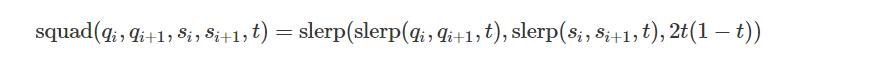
Conclusion
虽然四元数不好理解,但与使用矩阵或欧拉角来表示旋转相比,四元数提供了一些明显的优势:
- 使用SLERP或SQUAD的四元数插值方式,提供了在空间中方向与方向之间平滑插值的方法。
- 通过四元数可以进行旋转间的串联,它比通过矩阵间组合的方式所表示的旋转效率会更快。
- 对于归一化后的四元数,旋转的逆可以通过对四元数的向量部分取反来求取,但是如果要计算矩阵的逆效率是很慢的,除非矩阵是正交的。
- 将四元数转换为矩阵会比欧拉角稍微快一些。
- 空间占用上也比矩阵更有优势,四元数只需要4个数字(如果是标准化后的四元数则只需要3个,实数部分可以在运行时计算)来表示,而一个矩阵至少需要9个值才能表示旋转。
然而四元数也有它的一些缺陷:
- 四元数可能会因为浮点的舍入错误变无效,但是这类型的错误可以通过重新标准化四元数来解决。
- 使用四元数的最大问题是它们难以理解。希望读完这篇文章后,这个最大问题能够得到解决。
有不少数学库实现了四元数,其中GLM就是它们的典型。如果您有兴趣在自己的应用程序中使用四元数,我推荐使用这个库。
Download the Demo
文章原作者创建了一个小演示,演示如何使用四元数旋转空间中的物体。需要使用Unity打开。
本文翻译自: Understanding Quaternions