如果你是这个博客的长期读者，或许已经注意到一些反复出现的主题。逆运动学（Inverse Kinematics）无疑是其中之一——我曾用整个系列文章探讨如何将其应用于机械臂和触手机器人。不过，如果你没读过之前的系列也无需担心：这个新系列将自成一体，因为它会从一个全新的视角重新审视逆运动学问题。
介绍
我们经常习惯于与周围世界互动，以至于很容易忽略移动我们手和手臂的系统究竟有多复杂。在学术文献中，控制机械臂的任务被称为 逆运动学。运动学代表运动，而“逆”这个词指的是我们通常不直接控制手臂本身。我们所控制的是旋转各个关节的电机。逆运动学的任务就是决定如何驱动这些电机以将手臂移动到特定位置。在其一般形式中，这是一个挺有挑战性的任务。为了感受到这个挑战有多大，可以考虑像QWOP、GIRP甚至是登月小艇这样的游戏，在这些游戏中我们直接操控的是类似推进器的物件从而让其间接到达目的地。
通过操控移动执行器的这类功能甚至早于机器人学领域概念之前就早已存在。几个世纪以来，数学家和工程师一直在努力研发无数的解决方案。大多数3D建模软件和游戏引擎（包括Unity）都带有一系列工具，允许对类人或类狗的机械或生物进行适配。然而，对于特殊部分（如机械臂、尾巴、触手、翅膀等），通常不会提供内置的解决方案。
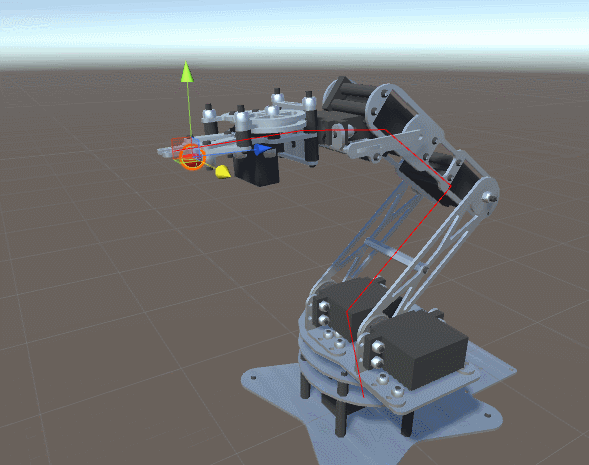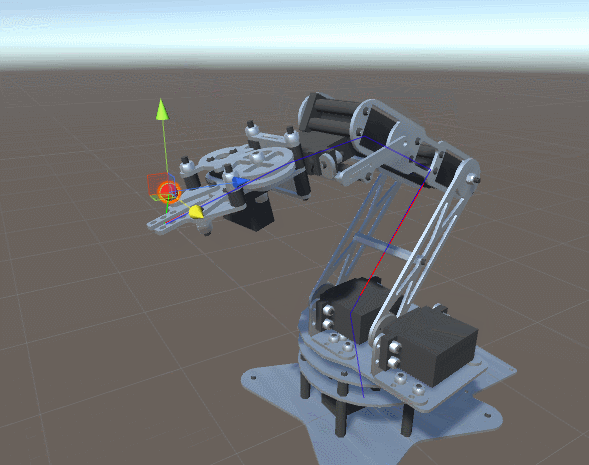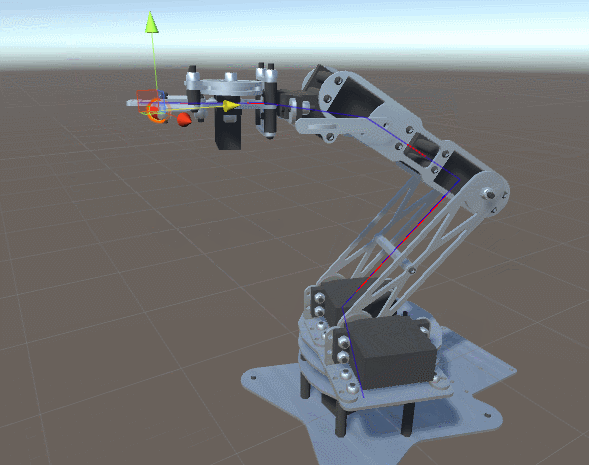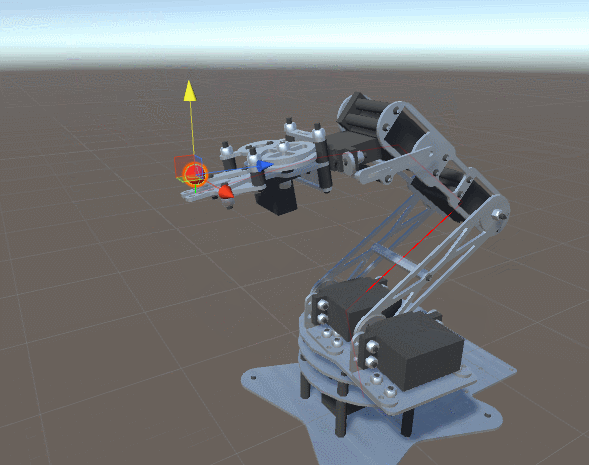
这就是为什么在之前关于程序动画和逆运动学的系列中，我们介绍了一种非常通用且有效的方法，这种方法理论上可以适用于任何情形。但是，更广的通用性意味着需要牺牲更多的效率。之前的系列收到的主要反馈是它太耗时了，无法同时用于成百上千个角色。正因为如此，我决定开启一个新的系列，专门针对具有2自由度手臂的逆运动学。本文中我们所学到的技术会非常高效，真的可以同时应用于几十个以上的角色上。
逆运动学
让我们想象一个有两段骨骼和两个关节的机械臂，就像下面图中看到的那样。在手臂的末端，是我们想要控制的 末端效应器（end effector）。我们无法直接控制末端效应器的位置；我们只能旋转关节。逆运动学的问题就是要找出旋转这些关节的最佳方式，以将末端效应器移动到期望的位置。
提出的这个新系列的解决方案仅适用于具有两个关节的机械臂。在学术文献中，这类机械臂通常被称为具有两个自由度。通过观察下图，你会非常清楚原因何在。具有两个自由度的机械臂可以被建模成一个三角形，而三角形是几何学中最常被研究的几何图形之一。
让我们更正式地定义一下这个问题。假设有两个关节，分别标记为A和B（在图中都用黑色表示），这两个关节可以分别绕着它们的轴旋转一定的角度，这里标记为A（用蓝色表示）和B（用绿色表示）角度。这种旋转会导致机械臂的末端效应器移动到另一个位置C。
内角
我们可以通过三点A、B和C构造一个具有三个内部角度α、β和γ的三角形，如下所示。这里，点A和B代表两个关节的位置，而点C代表末端效应器的位置。
虽然这三个角的角度是未知的，但所有边的长度都是已知的。
- 线段AB表示上臂，长度为c；
- 线段BC表示前臂，长度为a；
- 线段CA表示肩关节到手的距离，长度为b。
知道三角形的三边就足以找到它所有的角度。这得益于余弦定理，它是勾股定理的一个推广，适用于不一定是直角的三角形。
控制机械臂所需的两个角度是α 和β。让我们从α 开始，它可以通过对α 应用余弦定理来计算：
展开上式后得到：
现在需要使用反余弦函数（也被称为 arccosine）来找到α：
使用相同的步骤，我们可以再次应用余弦定理来找到β：
关节角
使用余弦定理，我们计算出了α 和β 的值，它们是机械臂形成的三角形的内角。然而，实际上我们需要的角度是 A（用蓝色表示）和 B（用绿色表示）。
让我们先来计算角度 B，这相对简单一些。从上述图示可以明显看出，β 和 B 的和等于180°（即π 弧度）。这意味着：
计算角度 A 并没有复杂很多，但这里我们需要考虑额外的角度 A'（用紫色表示），它是线段AC与参考方向（例如水平方向）之间的夹角。这个角度 A' 可以使用反正切函数来计算。
通过上式我们就得到了角度 A 的计算公式。
角度 A、A' 和 B 的正负在很大程度上都是可能的取值，并且取决于每个关节的具体运动方式。根据图示来理解可能会有困惑，明明α是A与A'的和，为什么上式却是α与A'的和才是A的角度。回顾2D极坐标对atan(y, x)的解释，我们知道它的取值范围在-PI ~ PI区间。根据上图的图示可知, Cy-Ay与Cx-Ax都为负数，所以落在了第三象限上，所以A'的角度实际上在图示所示的位置是负角度。
逆运动学问题通常有多个解决方案。即使在这个只有两个自由度的情况下，我们也存在两种不同的解决方案。
虽然角度 A 和 B 确实不同，但推导过程基本上保持不变，唯一的例外是公式 (13) 和 (11)。
接下来…
这篇文章结束了关于具有两个自由度的机械臂逆运动学数学介绍。
下一篇文章将探讨如何使用推导出的方程在Unity中高效地移动机械臂。
