求最小包围球: Welzl's algorithm

Question

通过计算模型顶点的中心点并找出点与中心的最大距离，可以很容易地得到一个包围一组顶点的球体。如果点的分布不均匀或者集中在网格的一端，这样的计算会导致边界体积大于所需。通过AABB计算球体通常能更好地接近网格顶点占用的体积。然而，该方法也不能给出具有最小体积的最佳球体。

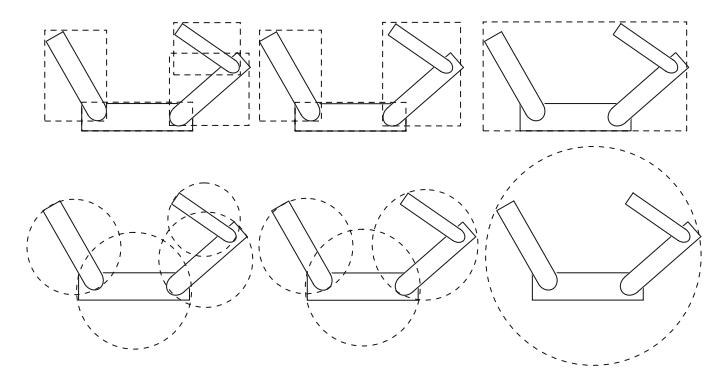
要求取最小圆或球的问题，可以运用到的算法是Welzl algorithm，关于它算法的详细信息可参考下面链接：

Sunshine's Homepage - Welzl's Algorithm

Welzl算法是一种增量方法，用于计算给定n个顶点 Sn= {P0, P1, ... , Pn-1} 的最佳包围球。该算法基于这样一个原则：如果点集 Si={P0, P1, ... , Pi-1} 的最小包围球为Di，那么Di需要包含位于球体Di之外的另一个点Pi，则新的最小边界球Di+1必须在其球面上包含Pi点。下图是一张二维示意图：

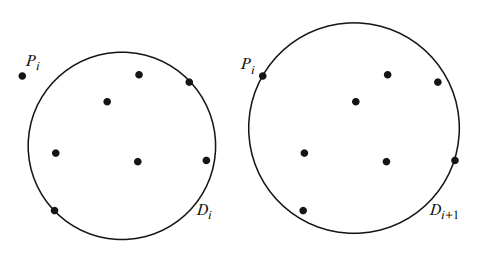
根据这个原则，我们可以先简单以最小圆分析，可以取三个点建立一个圆，这三点有共线与不共线的情况，共线可取距离最远的两个点为直径建立圆，不共线则三个点即可确立外接圆。接着遍历所有点，对于给定遍历到的点p：

如果点p在圆内，则最小覆盖圆不做改变。
如果p点在圆外，根据上述原则，该点必须在要求取的最小覆盖圆上，又因为3点才能确立外接圆，所以需要枚举p之前的点来确立剩下的两个点。直到找到另外两个点，使得与p点确立的圆能将所有点包含在里面。

下述伪代码给出了Welzl算法作为递归函数的实现。可以通过 minSphere(S, n, B, 0)方式调用；其中变量S代表集合Sn，n为点集的数量，B是球面上的点集，初始值为空数组，nb为球面上点集数量。如公式所示，最小球体Dk是以k-1范围点的最小球体Dk-1来定义的，k的初始值为n。

Sphere minSphere(Point pt[], int np, Points bnd[], int nb) {
    if(np == 1) {
        if(nb == 0) return Sphere1pt(pt[0]);
        if(nb == 1) return Sphere2pts(pt[0], bnd[0]); 
    } else if(np == 0) {
        if(nb == 1) return Sphere1pt(bnd[0]);
        if(nb == 2) return Sphere2pts(bnd[0], bnd[1]);  
    }
    if(nb == 3) {
        return Sphere3pts(bnd[0], bnd[1], bnd[2]);
    }
    Sphere D = minSphere(pt, np-1, bnd, nb);
    if(D.isInside(pt[np-1])) {
        return D;
    }
    bnd[nb] = pt[np-1];
    nb++;
    D = minSphere(pt, np-1, bnd, nb);
    return D;
}

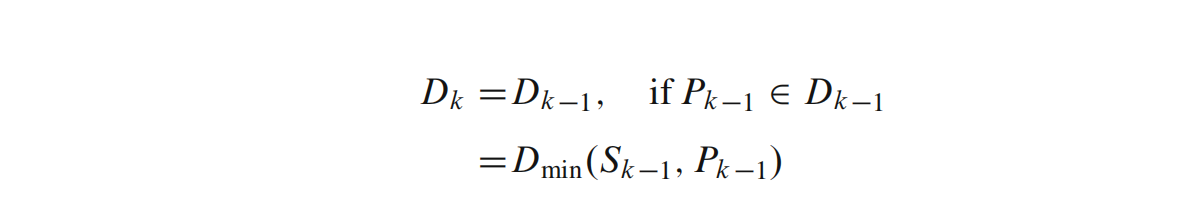
isInside函数定义了点是否在球体内部的判断方法，可以通过判断对应点与当前球心的距离，如果大于半径则点在球外。

其中Dmin(Sk-1, Pk-1)是包含Sk-1点集的最小包围球，并且点Pk-1在球面上。在运算的任何阶段，最小球体由集合(c，r）表示，其中c是球体中心，r是半径。上述伪代码中球体由函数Sphere1pt()、Sphere2pts()等定义，逻辑如下：

Sphere1pt(P): 中心点c=P，半径r=0；

Sphere2pts(P, Q): 中心点c = (P+Q)/2，半径r=|c-P|；

Sphere3pts(P, Q R)相对复杂，下面展开分析。

如上所述，通过两点确定的球体，是两点位于直径两端的最小包围球。在球体上径向相对的对称点称为对跖点。对于三个点 P、Q、R，球体将通过这些点作外接球。在这种情况下，球体的中心和半径与通过这些点的圆的中心和半径相同。构成三角形 PQR 的顶点 R 处的内角通过下式计算：

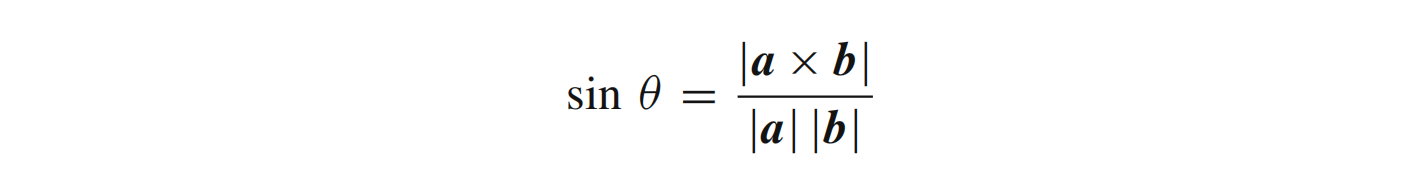
其中 a = P - R，并且 b = Q - R。

根据正弦定理：

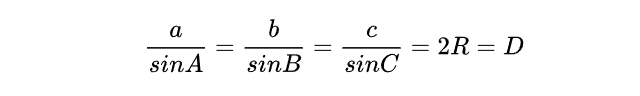
通过这三个点得到的圆(以及球体)半径为：

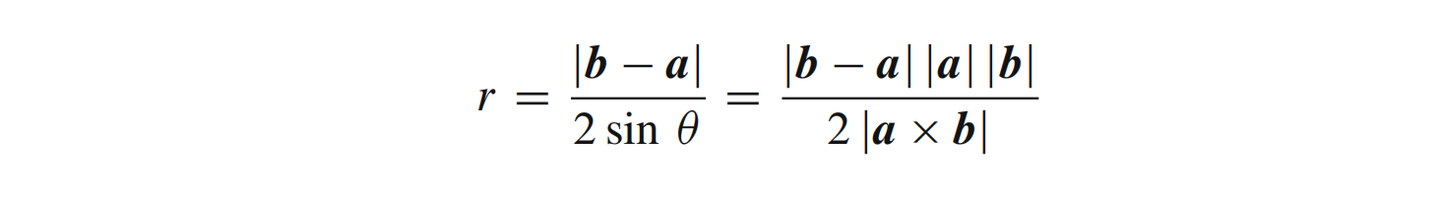
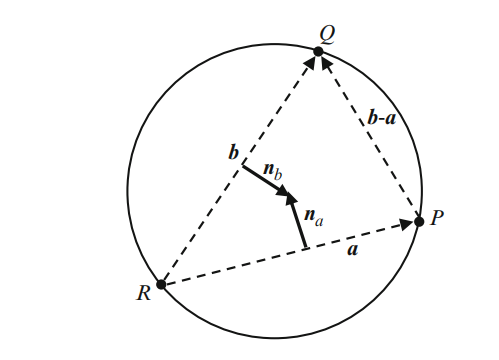
通过三个点的最小球体

上图中通过a与b的垂直平分线的交点可确立外接圆的圆心，其中a与b的垂直平分线可通过下述方式求取：

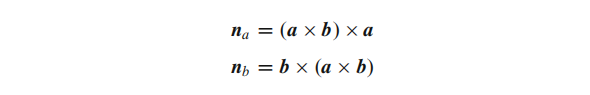
中心点的坐标可利用上述结果求取：

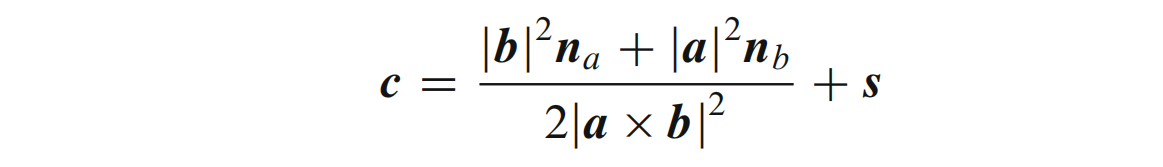
其中s代表点R坐标。

求最小包围球: Welzl's algorithm

0 Answers