CPU实现一套软光栅的核心实现往往是(有些实现会涉及到逐片元操作,下图忽略):
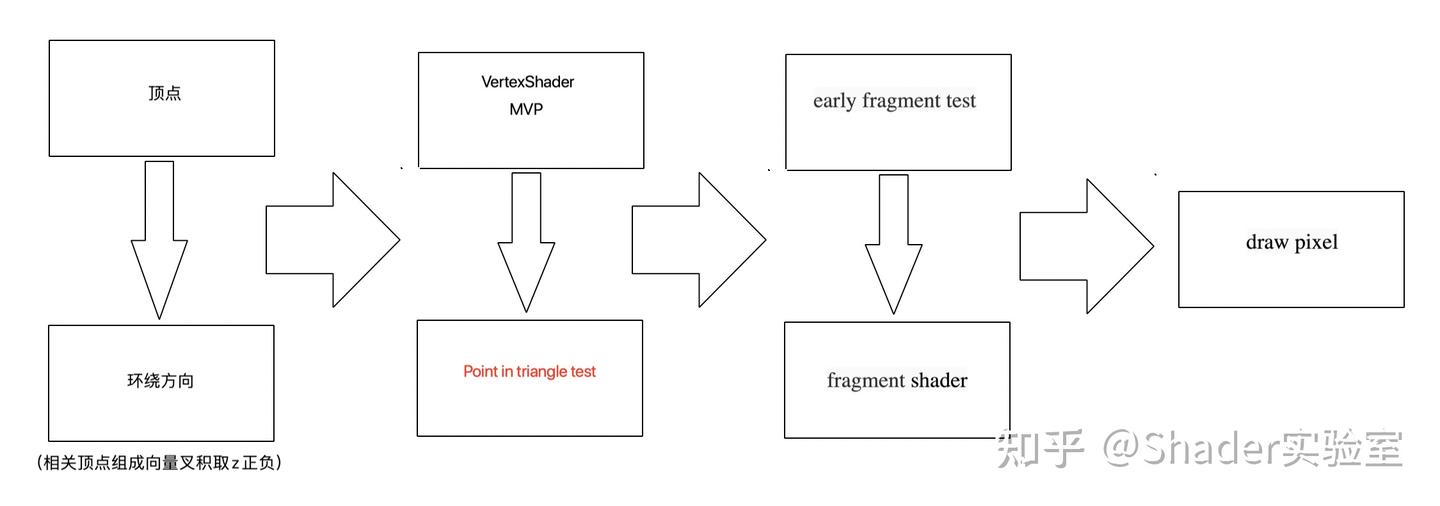
而我们主要讨论的是如何判断点在三角形内。
要判断一个点在三角形内一般有如下三种方法:角度累加,Crossproduct Side Algorithm,重心坐标。
角度累加
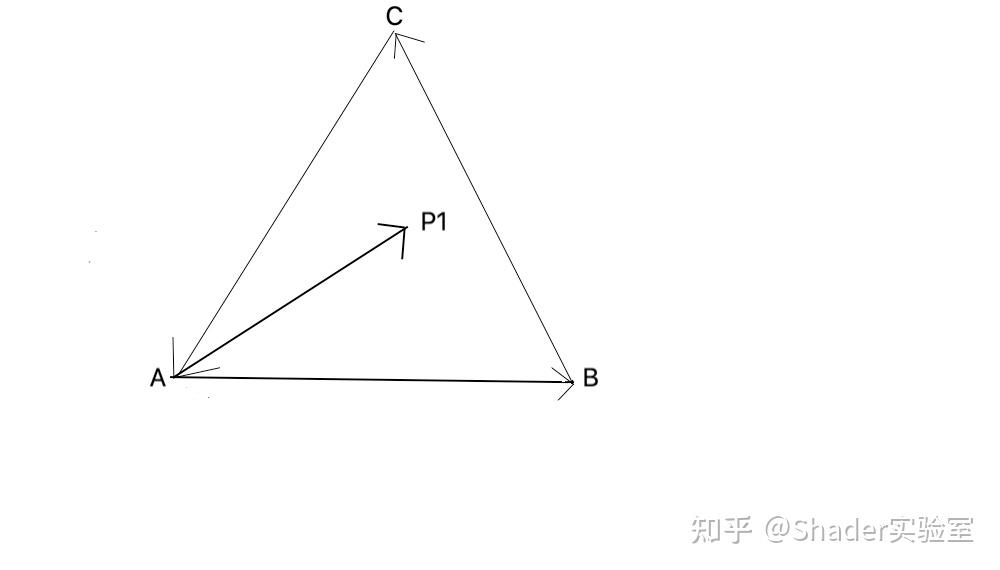
有一点P,P点与三角形三个顶点的连线,构成的角度为360度,我们可以认定该点在三角形内,否则为三角形外,如图:
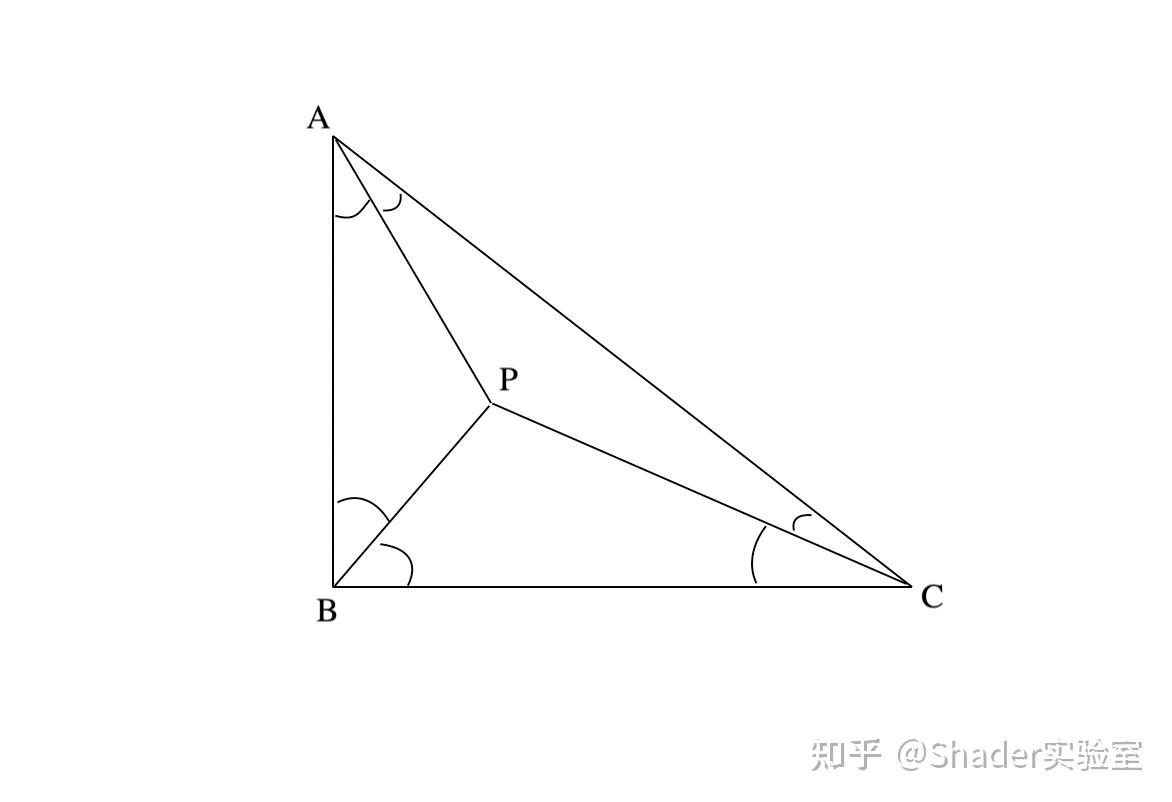
上图可发现需要求取六个角的角度,角度计算可通过向量点乘的方式,如:
$$
∠PCA=arccos((CP⋅CA)/(|CP|∗|CA|))
$$
再通过上述的方式把6个角的角度相加,结果为π时,则点在三角形内。
为了简化三角形中角度的运算,可以通过 ∠APB 与 ∠APC 以及 ∠BPC 三个角度的累加运算获得。
但是该方法由于涉及到浮点数的运算,很难使得最后的运算结果等于2π,并且它的运算效率较慢,在运算效率要求较高的光栅化中,该方法并不适合。
Crossproduct Side算法
点与边存在三种关系:点在边上,点在边的左边以及点在边的右边。而计算这三种关系的过程就是通过“Crossproduct side算法",这个算法名字不是正式的叫法,但是为了更好的描述,取一个直观的名字是有必要的。
该算法的计算过程通过向量叉乘的方式,但是二维向量对叉乘算法并没有太多相关的定义,但是通常可以通过下面的方式定义:
$$
Z = vx1 * vy2 - vy1 * vx2
$$
这是三维向量叉乘计算时求取Z分量的方法(也是行列式的求法)。
这里的Z是标量,叉乘不是向量么?为什么可以通过判断标量的正负来判定指向的方向呢?我们可以取两个二维向量,分别为A(1, 2)与B(3, 1)。
此时A向量可以看成:A(1, 2, 0);
B向量可以看成: B(3, 1, 0);
那么cross(A, B)可得C(0, 0, -5);
由于A与B向量的z值都为0,所以叉乘后向量的x,y值也为0,那么我们只需要计算Z值即可判定两个二维向量叉乘后所指向的方向。
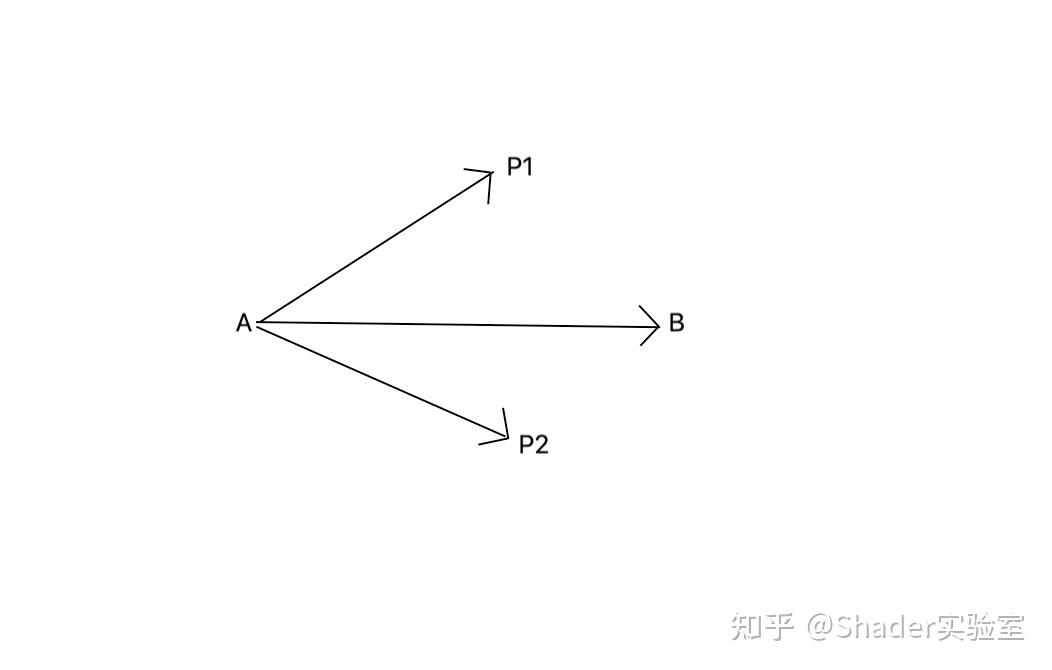
以右手坐标系举例,当AB向量叉乘于AP1向量,Z指向正在看屏幕的自己;当AB向量叉乘于AP2向量,Z与看向屏幕的方向相同。到这其实已经可以得出结论:当AB向量与其上方的任意点形成的AX1向量叉乘,Z的指向必然指向看屏幕的自己;反之当AB向量与其下方的任意点形成的AX2向量叉乘,Z必然与看向屏幕的方向相同;当点在AB上,则Z的值为0。
那么剩下的唯一的问题是:如何判定Z指向的哪个方向是我们想要的指向?这时候就可以利用三角形的另一个顶点C, 当AB向量叉乘于AC向量,与AB向量叉乘于AP1向量,具有相同的指向,那么就可以认为P1点与C点同侧;同样的,CA向量叉乘于CP1向量,与CA向量叉乘于CB向量,具有相同指向,那么就可以认为P1点与B点同侧;最后,BC向量叉乘于BP1向量,与BC向量叉乘于BA向量,具有相同指向,那么就可以认为P1点与A点同侧。总结上面的结论,当上面的所有条件都满足,则可以认为P1点在三角形内。
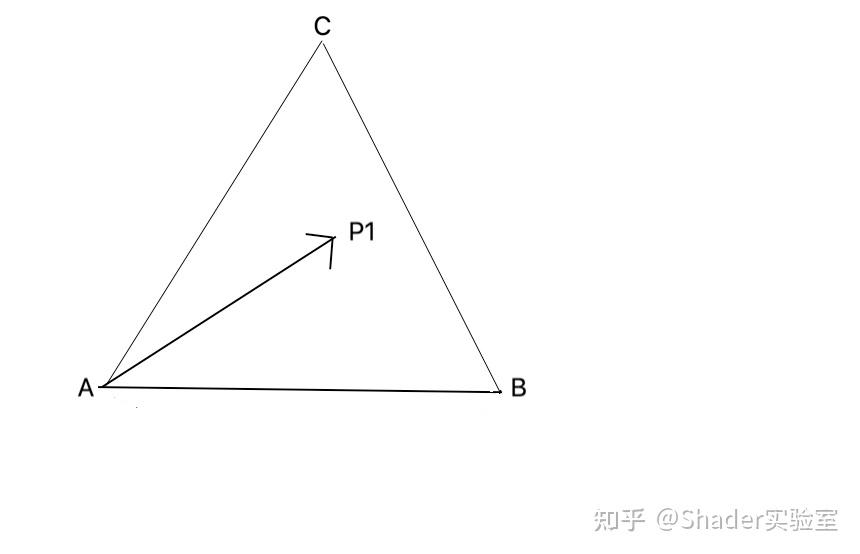
上述条件中,可以发现:AB向量叉乘AP1向量,BC向量叉乘于BP1向量,以及CA向量叉乘CP1向量,它们都同时通过右手法则计算Z的指向,并且得出的Z指向相同时(同时>0或同时<0),则可以认为P1点在三角形内,这样计算过程就可以减少一个比较操作(与三角形另一个顶点是否同向的比较)。
重心坐标
Crossproduct Side方法的优点在于它易于理解,便于记忆,且只需要记住目标点与三条边的关系即可。接下来介绍另一种验证点在三角形的方法, 它通过重心坐标计算,由于它执行效率更快,很多光栅化,甚至是模型线框的实现都可以见到它的身影。
重心坐标的实现也有很多方式,主要分析其中的一种实现。
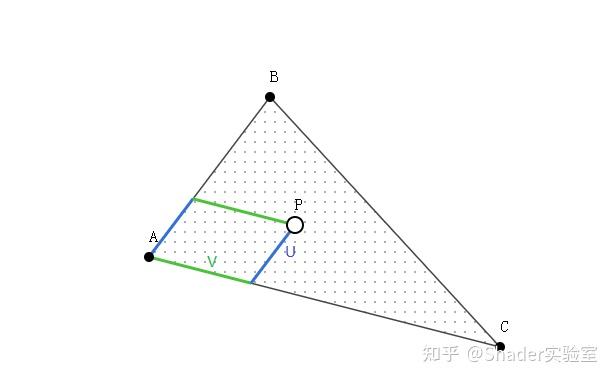
由上图可知:
$$
AP = uAB + vAC
$$
又因为:
$$
P - A = u(B - A) + v(C - A)
$$
所以:
$$
P = (1 - u -v)A + uB + vC
$$
这是得出的第一个公式,先记下,稍后要用。
因为:
$$
AP = uAB + vAC
$$
所以:
$$
uAB + vAC + PA = 0
$$
上式的0代表0向量。
上式可分解为向量点乘的形式:
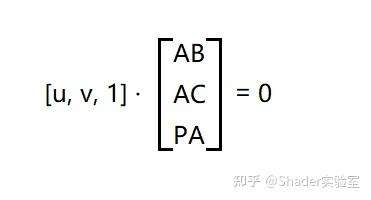
大家都知道点乘是两个向量的点乘,而向量内部的每个分量都是标量,但是仔细观察上式,会发现右边的向量,内部的每个分量都是一个向量,这个在数学当中真的很难找到定义,不过没关系,既然右边向量的每个分量都是向量,那就把它拆解看看?
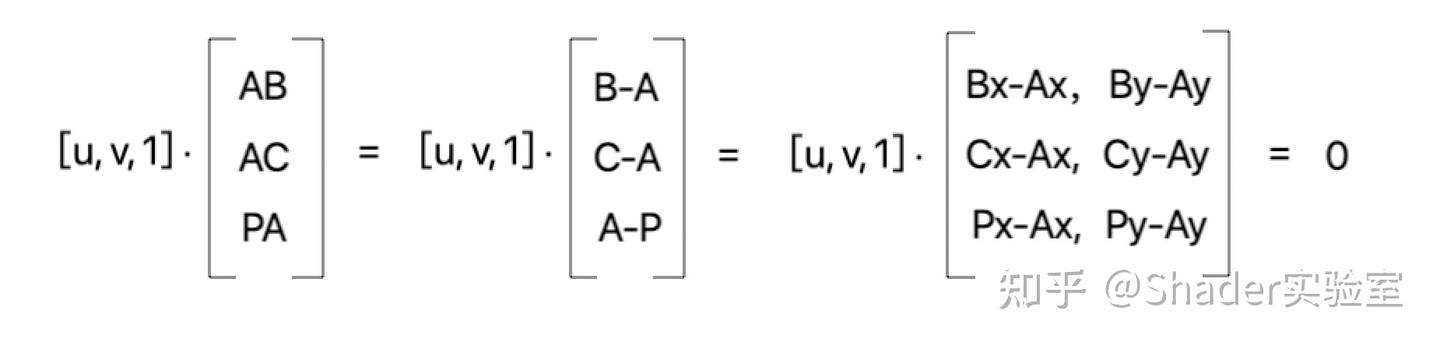
(注意:此时上面的0依旧是0向量)拆解后发现右边的向量居然可以被拆解为3x2的矩阵,剩下的就是矩阵乘法:
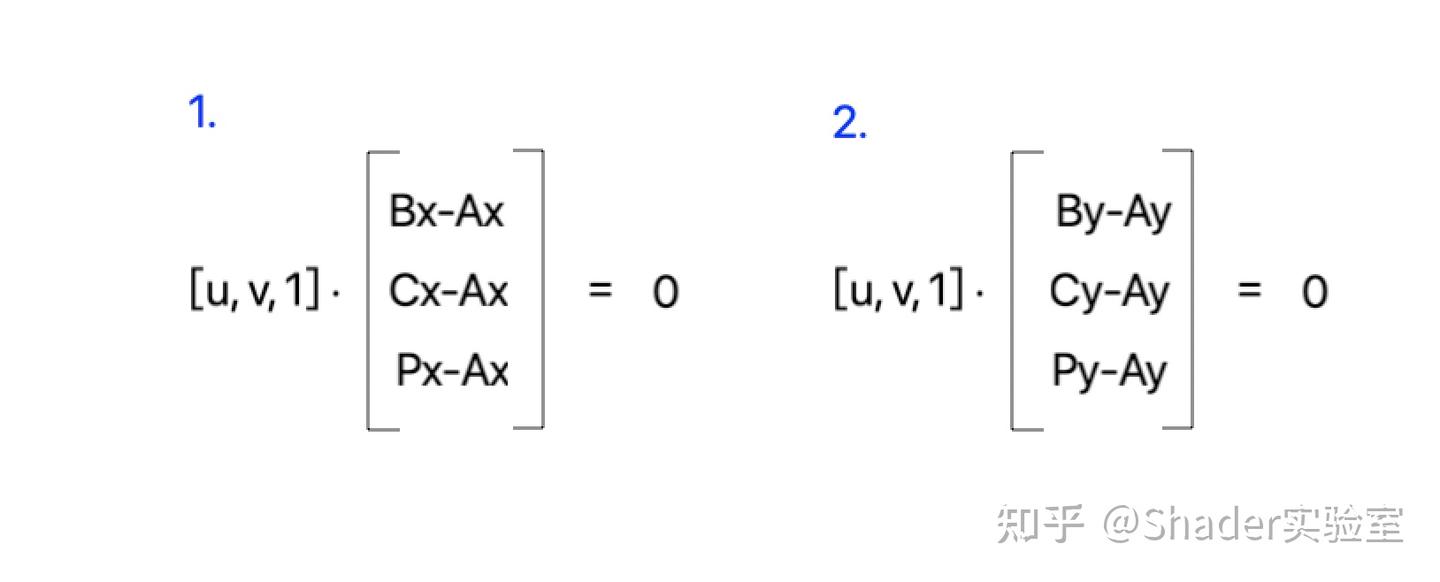
(注意:此时上面的0是标量),上图中1与2的式子类似,以1为例分析,由于[u, v, 1]点乘于[Bx-Ax, Cx-Ax, Px-Ax]等于0,又根据向量点乘的公式:
$$
A · B = |A||B|cos\theta
$$
又因为[u, v, 1]与[Bx-Ax, Cx-Ax, Px-Ax]的模长不可能为0(你们都懂),所以只有A向量与B向量的夹角为90度时,才为0;所以[u, v, 1]与[Bx-Ax, Cx-Ax, Px-Ax]相互垂直,同理[u, v, 1]与[By-Ay, Cy-Ay, Py-Ay]也相互垂直。
根据两向量叉乘可得到一个与该两向量垂直的向量,可得:
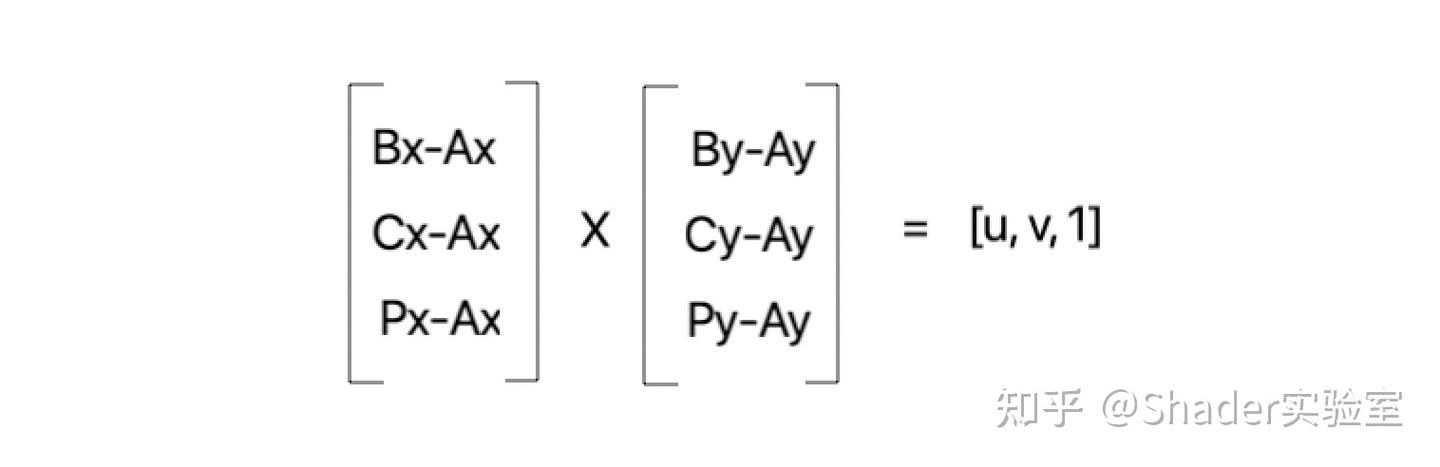
由于叉乘的结果是浮点数,所以向量[u, v, 1]中的z分量不一定会准确为1,由于z不会准确为1,假设结果为[x, y, z],那么u与v的结果如下:
(为什么?想象二维向量如果有第三个分量如何求取点?)结合第一个公式,可得最终P的结果:
$$
P = (1 - x/z -y/z)A + x/zB + y/zC
$$
要让P点在△ABC内,需要满足:
实例
// 顶点结构
struct VerInfo{
vec3 v1;
vec3 v2;
vec3 v3;
vec2 p;
vec2 uv1;
vec2 uv2;
vec2 uv3;
};
vec3 frag_color = vec3(0.,0.,0.);
// vertex
const vec3 vertices[6] = vec3[6](vec3(-0.4, 0.,0.),
vec3(0.4,0.,0.),
vec3(-0.3, 0.45, 0.),
vec3(0.42,0.,0.),
vec3(-0.3, 0.46, 0.),
vec3(0.5, 0.5, 0.)
);
// uvs
const vec2 uvs[6] = vec2[6](vec2(0.,0.),
vec2(1.,0.),
vec2(0.,1.),
vec2(0.,1.),
vec2(1.,0.),
vec2(1.,1.)
);
// indices
const int indices[6] = int[6](0,1,2,
4,3,5
);
// 获取重心坐标
vec2 getBary(vec3 v1, vec3 v2, vec3 v3, vec3 p) {
vec3 v12 = v2 - v1;
vec3 v13 = v3 - v1;
vec3 pv1 = v1 - p;
vec3 c1 = vec3(v12.x, v13.x, pv1.x);
vec3 c2 = vec3(v12.y, v13.y, pv1.y);
vec3 u = cross(c1, c2);
return vec2(u.x/u.z, u.y/u.z);
}
// 通过重心坐标判断点是否在三角形内
void triangle(VerInfo verInfo) {
vec3 v1 = verInfo.v1;
vec3 v2 = verInfo.v2;
vec3 v3 = verInfo.v3;
vec3 p = vec3(verInfo.p.x, verInfo.p.y, 0.);
vec2 bary = getBary(v1,v2,v3,p);
if(bary.x >= 0. && bary.y >= 0. && (bary.x + bary.y)<=1.) {
vec2 uv = (1.-(bary.x+bary.y))*verInfo.uv1 + bary.x*verInfo.uv2 + bary.y*verInfo.uv3;
frag_color += texture(iChannel1, uv).xyz;
}
}
// 绘制模型
void drawModel(vec2 p) {
for(int i = 0; i < 6; i+=3) {
vec3 v1 = vertices[indices[i]];
vec3 v2 = vertices[indices[i+1]];
vec3 v3 = vertices[indices[i+2]];
vec2 uv1 = uvs[indices[i]];
vec2 uv2 = uvs[indices[i+1]];
vec2 uv3 = uvs[indices[i+2]];
VerInfo verInfo = VerInfo(v1,v2,v3,p,uv1,uv2,uv3);
triangle(verInfo);
}
}
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
// Normalized pixel coordinates (from 0 to 1)
vec2 uv = fragCoord/iResolution.xy;
uv -= 0.5;
uv *=2.;
uv.x *= iResolution.x/iResolution.y;
drawModel(uv);
// Output to screen
fragColor = vec4(frag_color, 1.);
}
上述代码是在Shadertoy上简单编写的代码,这是链接地址。(要在PC端浏览器打开)
还有如下效果也部分用到重心坐标实现(看日期是去年6月份敲的,记得当时纯手打了两天^_^)这是地址,感兴趣的可以去看看实现:
为了完整性,贴出Crossproduct side算法实现:
boolean crossproductSide(aPoint: Vec2, bPoint: Vec2, cPoint: Vec2, pPoint: Vec2) {
let ab = this.cross(aPoint, bPoint, pPoint);
let bc = this.cross(bPoint, cPoint, pPoint);
let ca = this.cross(cPoint, aPoint, pPoint);
if((ab >= 0 && bc >= 0 && ca >= 0) || (ab <= 0 && bc <= 0 && ca <= 0)) {
return true;
}
return false;
}