向量是一个具有长度（或更正式地说，大小）和方向的实体。它可以直观地在笛卡尔坐标系中表示，在二维空间中分解为 x 和 y 两个分量，在三维空间中分解为 x、y 和 z 三个分量。
我们用加粗的小写字符表示一个向量，用相同的普通字符加上分量下标来表示其分量。例如：
表示一个二维向量。每个分量是对应坐标轴上从原点的距离。
物理引擎通常拥有自己轻量级、高度优化的数学库。例如，Bullet Physics 引擎有一个名为 Linear Math 的独立数学库，它可以单独使用，而无需依赖 Bullet 的物理模拟功能。该库包含表示向量和矩阵等实体的类，并且如果硬件支持的话，它会利用 SIMD 指令进行优化。
以下回顾了一些作用于向量的基本代数运算。
长度
长度（或大小）运算符用∣∣表示。根据著名的勾股定理（直角三角形定理），可以通过向量的分量计算其长度。例如，在二维空间中：
如果一个向量V=(Vx, Vy)，则其长度为：
取反
当一个向量被取反时，其长度保持不变，但方向变为完全相反。例如，给定一个向量：
取反后为：
加法与减法
向量可以相互相加或相减。两个向量相减等同于将其中一个向量加上另一个向量的相反数。在这些运算中，我们只需对每个分量进行相应的加法或减法运算。
所得的向量可以被可视化为指向两个原始向量首尾相连时所达到的相同终点：
标量乘法
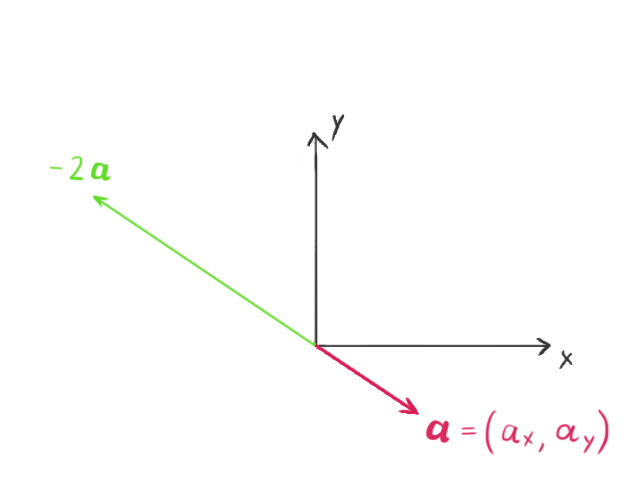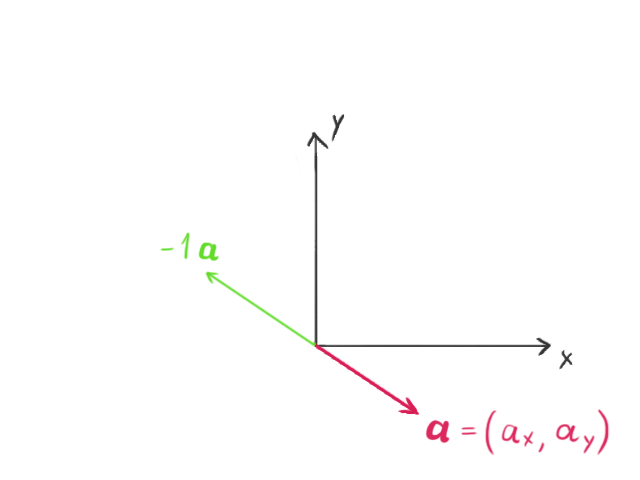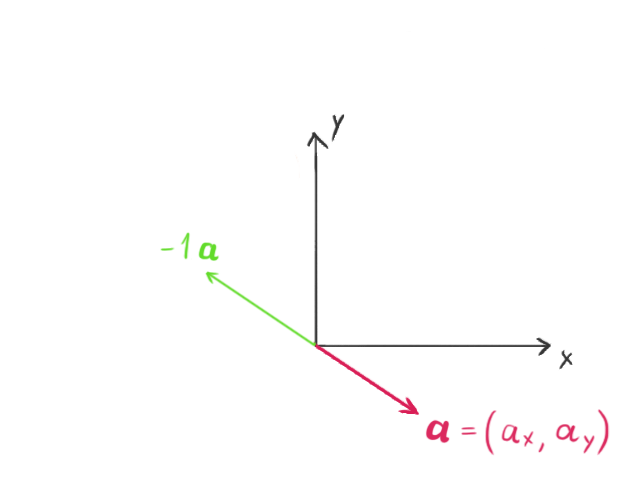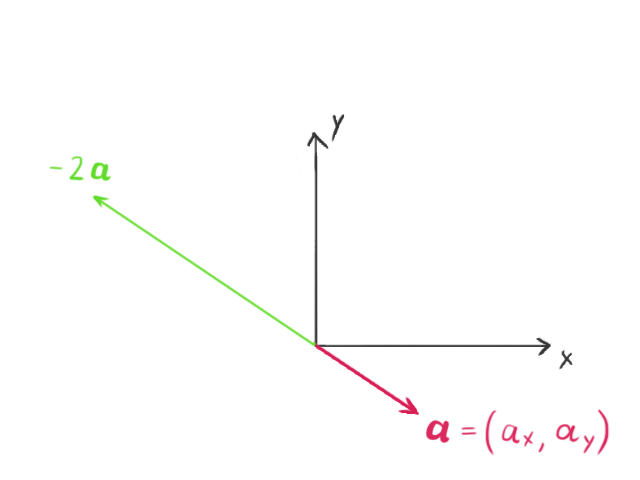
当一个向量与一个标量（在本教程中，标量简单地指任何实数）相乘时，向量的长度会按该标量的数值发生变化。如果标量为负数，向量的方向还会变为相反方向。
点积
点积运算接受两个向量作为输入，并输出一个标量值。它被定义为：
其中𝜃 是两个向量之间的夹角。从计算的角度来看，使用向量的分量来计算点积要简单得多，即：
点积的值等价于向量 a 在向量 b 上的投影长度乘以 b 的长度。这一操作也可以反过来进行，即取向量 b 在向量 a 上的投影长度，并乘以 a 的长度，结果是相同的。这意味着点积是可交换的——向量 a 与 b 的点积等于向量 b 与 a 的点积。
点积的一个有用性质是：如果两个向量正交（它们之间的夹角为 90 度），则点积的值为零，因为：
$$
cos90°=0
$$
叉积
在三维空间中，我们还可以通过叉积运算将两个向量相乘，输出另一个向量。叉积的定义如下：
叉积的长度可以表示为：
其中𝜃是向量 a 和 b 之间的最小夹角。叉积的结果是一个向量 c，它同时垂直于（正交于）a 和 b。如果 a 和 b 平行，即它们之间的夹角为 0° 或 180°，那么 c 将是零向量，因为sin 0=sin 180=0。
与点积不同，叉积不满足交换律。叉积中元素的顺序非常重要，因为：
结果向量的方向可以通过右手定则来确定。张开你的右手，将食指指向与向量 a 相同的方向，并将手掌调整为当你握拳时，四指能够从 a 的方向以最小夹角弯曲并指向 b 的方向。此时，你的大拇指所指的方向就是 a × b 的方向。
