在本章中，我们将涵盖以下内容：
- 使用顶点位移实现表面动画
- 创建粒子喷泉
- 利用TransformFeedback变换反馈创建粒子系统
- 使用实例化粒子创建粒子系统
- 利用粒子模拟火焰
- 利用粒子模拟烟雾
介绍
着色器让我们得以充分利用现代显卡的大规模并行架构。由于着色器具备变换顶点坐标的能力，因此可被用于在其内部直接实现部分动画相关功能。如果动画算法能够被合理地并行化，从而在着色器中执行，就能带来一定的效率提升。
在着色器程序中实现动画的一大难点，在于难以写入更新后的顶点坐标。着色器的设计初衷并非支持向任意缓冲区写入数据（帧缓冲区除外）。因此，许多开发者会灵活运用帧缓冲对象（FBO） 与纹理对象来存储着色器的输出数据。
不过近年来，OpenGL 新增了一项特性，支持将顶点着色器输出变量的值写入任意一个或多个缓冲区。这项特性被称为Transform Feedback 变换反馈。
在本篇中，我们将探讨若干在着色器中实现动画的示例，核心聚焦于粒子系统。
- 第一个示例《基于顶点位移实现动画》，演示了如何通过基于时变函数变换对象的顶点坐标来实现动画效果。
- 在《创建粒子喷泉》这一实例教程中，我们将构建一个恒加速度作用下的简易粒子系统。
- 《使用变换反馈创建粒子系统》则通过示例说明如何在粒子系统中运用 OpenGL 的变换反馈功能。
- 《使用实例化粒子创建粒子系统》这一实例教程，会展示如何借助实例化渲染，为大量复杂对象添加动画效果。
最后两个实例教程，重点呈现了用于模拟烟雾、火焰等复杂真实物理系统的粒子系统实现方案。
基于顶点位移实现动画
利用着色器实现动画的一种简单直接的方式，是在顶点着色器中基于某种Time-Dependent Function时变函数对顶点进行变换。OpenGL 应用程序提供静态几何图形，顶点着色器则借助当前时间（以统一变量（uniform variable） 的形式传入）修改这些几何图形。这一做法将顶点坐标的计算任务从 CPU 转移到 GPU，并充分利用图形驱动所提供的所有并行处理能力。
本示例中，我们将基于正弦波对细分后的四边形顶点进行变换，以此创建一个起伏的波浪表面。我们会向渲染管线传入一组三角形，这些三角形共同构成 x-z 平面上的平坦表面；而在顶点着色器中，我们将基于时变正弦函数调整顶点的 y 坐标，并计算变换后顶点的法向量。下图展示了预期达成的效果（可以自行想象：波浪正从左至右沿该表面移动）。
我们可以使用噪声纹理来基于随机函数对表面进行动画。（有关噪声纹理的详细信息，请参见Shader实验室相关文章）。
在深入代码实现之前，我们先梳理一下所需用到的数学原理。
我们将把曲面的 y 坐标变换为当前时间与模型空间 x 坐标的函数（即 y 坐标由这两个变量共同决定）。为此，我们会采用基础的平面波方程（如下图示）。
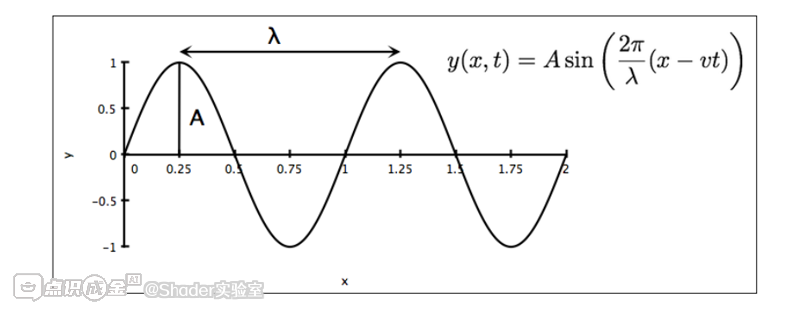
其中，A 为波的振幅（波峰的高度），λ（拉姆达）为波长（相邻波峰之间的距离），v 为波的传播速度。前述图示展示了 t = 0 且波长为 1 时该波的示例效果。我们将通过统一变量（uniform 变量） 来配置这些系数。
为了让曲面呈现出正确的着色效果，我们还需要计算顶点变换后的位置的法向量。该法向量可通过对上述函数求（偏）导数得到，最终推导得出如下方程：
$$
\mathbf{n}(x,t) = \left( -A\frac{2\pi}{\lambda} \cos\left( \frac{2\pi}{\lambda}(x - vt) \right), 1 \right)
$$
当然，在将上述向量代入着色模型进行计算之前，必须先对其做归一化处理。
准备工作
配置你的 OpenGL 应用程序，使其渲染出 x-z 平面上的平坦细分曲面。使用的三角形数量越多，最终呈现的效果会越理想。同时，可采用你偏好的任意方式记录动画时间，并通过名为 Time 的统一变量（uniform 变量），将当前时间传递给顶点着色器。
其余关键的统一变量（uniform 变量）为前述波方程的各项系数：
- K：波数（计算公式为 2π/λ）
- Velocity（速度）：波的传播速度
- Amp（振幅）：波的振幅
配置程序，为选定的着色模型提供这些适配的统一变量。
如何做
使用以下代码创建顶点着色器：
#version 400
// 顶点位置输入（布局位置0）
layout (location = 0) in vec3 VertexPosition;
// 输出：变换后的顶点位置（相机空间）
out vec4 Position;
// 输出：变换后的法向量（相机空间）
out vec3 Normal;
// 动画时间（由CPU传入的uniform变量）
uniform float Time;
// 波方程参数
uniform float K; // 波数
uniform float Velocity; // 波的传播速度
uniform float Amp; // 波的振幅
// 模型视图矩阵（将顶点转换至相机空间）
uniform mat4 ModelViewMatrix;
// 法向量矩阵（法向量的模型视图变换，保证正交性）
uniform mat3 NormalMatrix;
// 模型视图投影矩阵（将顶点转换至裁剪空间）
uniform mat4 MVP;
void main()
{
// 将顶点位置转换为齐次坐标（w分量为1.0）
vec4 pos = vec4(VertexPosition, 1.0);
// 计算正弦波的相位因子：u = 波数 × (x坐标 - 波速×时间)
// 核心作用：模拟波浪沿x轴正方向（Velocity为正）移动
float u = K * (pos.x - Velocity * Time);
// 基于正弦函数修改y坐标，实现波浪起伏
pos.y = Amp * sin(u);
// 计算法向量：先求波函数对x的偏导，再构造法向量并归一化
vec3 n = vec3(0.0);
// 法向量xy分量：(-K×A×cos(u), 1.0) 归一化，z分量保持0（x-z平面波浪）
n.xy = normalize(vec2(-K * Amp * cos(u), 1.0));
// 将顶点位置和法向量转换至相机空间，传递给片元着色器
Position = ModelViewMatrix * pos;
Normal = NormalMatrix * n;
// 最终输出裁剪空间顶点坐标（OpenGL固定要求）
gl_Position = MVP * pos;
}
创建一个片元着色器，该着色器基于 Position 和 Normal 变量，使用你选择的任意着色模型计算片元颜色(如Blinn-Phong)。
原理
顶点着色器接收顶点的位置信息，并利用此前讨论过的波动方程更新其 y 坐标。在前三条语句执行完毕后，变量 pos 本质上是输入变量 VertexPosition 的副本，仅更新了其中的 y 坐标。
随后，我们通过前文的公式计算法向量，将计算结果归一化后存入变量 n 中。由于该波实际为二维波（其传播不依赖 z 轴），因此法向量的 z 分量值为 0。
最后，我们将新的顶点位置和法向量转换为相机坐标系下的数值后，传递给片元着色器。和常规操作一致，我们也会将裁剪坐标系下的顶点位置传入内置变量 gl_Position 中。
更多
在顶点着色器中修改顶点位置，是将部分计算任务从 CPU 转移到 GPU 的一种简便方法。这种方式还能避免为修改顶点位置，而在 GPU 内存与主内存之间传输顶点缓冲区的操作。
该方法的主要缺点在于：如果更新后的顶点位置需要用于后续额外处理（例如碰撞检测），CPU 端将无法直接获取这些数据。不过，也有多种方法可以将这类数据回传给 CPU。其中一种技巧是灵活运用帧缓冲对象（FBOs），从片元着色器中读取更新后的顶点位置。在下一小节中，我们将介绍另一种技术，它会用到 OpenGL 的一项较新特性 ——变换反馈（transform feedback）。
创建一个粒子喷泉
在计算机图形学中，粒子系统是一组用于模拟各类 “模糊” 效果体系的对象，可还原烟雾、液体喷射、火焰、爆炸或其他类似现象。每个粒子都被视为仅具备位置信息、无尺寸属性的点对象；通常情况下，粒子会被渲染为点精灵（采用 GL_POINTS 图元模式）。
每个粒子都有完整的生命周期：从 “诞生” 开始，按照预设的一组规则完成运动动画，随后 “消亡”；消亡后的粒子可被重新激活，再次完整经历整个生命周期。通常而言，粒子之间不会产生交互行为，也不具备反光特性；粒子也常被渲染为单个带纹理、面向相机且具备透明效果的四边形。
在单个粒子的生命周期内，其运动轨迹会遵循一组预设规则来驱动。这些规则通常包含基础运动学方程—— 这类方程用于定义粒子在恒定加速度作用下的运动规律（例如重力场环境）。除此之外，我们还可以纳入风力、摩擦力或其他影响因素的计算逻辑。粒子在生命周期内，其形状或透明度也可能发生动态变化。一旦粒子的 “存活时长” 达到阈值（或运动到指定位置），它就会被判定为 “消亡” 状态，随后可被回收复用，再次参与新一轮的粒子生命周期循环。
在本示例中，我们将实现一个相对简易的粒子系统，模拟出喷泉喷水的视觉效果。本示例中的粒子不涉及 “回收复用” 机制：当粒子到达生命周期终点时，我们会将其渲染为完全透明的状态，使其达到视觉上完全不可见的效果。这种设计会让喷泉呈现出 “有限喷射时长” 的特点，仿佛其喷射的水源是有限的。在后续的示例中，我们会介绍一些优化方案，通过粒子回收复用的方式来改进这个粒子系统。
以下是一组连续的帧序列图像，展示了这个简易粒子系统的输出效果：
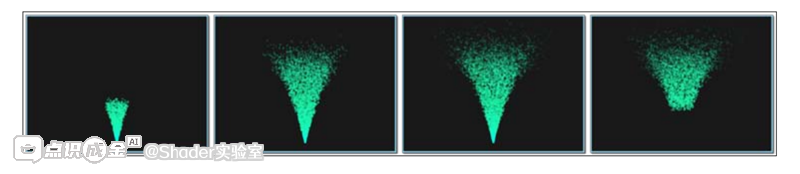为了实现粒子的动画效果，我们将采用适用于恒定加速度作用下物体的标准运动学方程。
$$
\mathbf{P}(t) = \mathbf{P}_0 + \mathbf{v}_0 t + \frac{1}{2}\mathbf{a} t^2
$$
上述方程描述了粒子在时刻 t 的位置。P0 代表初始位置，v0 代表初始速度，a 则为加速度。
我们将所有粒子的初始位置统一设定为坐标原点 (0,0,0)。初始速度会在设定的数值区间内随机生成。每个粒子的生成时间存在细微差异，因此我们在上述方程中使用的时间参数，是相对于该粒子生成时刻的相对时间。
由于所有粒子的初始位置完全相同，我们无需将其作为着色器的输入属性传入。取而代之的是，我们只需向着色器传入另外两个顶点属性：初始速度和生成时刻（即粒子的 “诞生时间”）。在粒子到达诞生时间之前，我们会将其渲染为完全透明的状态；粒子诞生之后，我们便用上述方程计算它的位置，方程中的时间参数 t 取相对时间（计算方式为：Time – StartTime）。
我们将把每个粒子渲染为带纹理的点精灵（采用 GL_POINTS 图元模式）。为点精灵应用纹理的操作十分简便 —— 因为 OpenGL 会自动生成纹理坐标，并通过内置变量 gl_PointCoord 将这些坐标传递给片元着色器供其使用。
同时，我们会让点精灵的 Alpha 值随粒子的存活时长呈线性衰减，以此实现粒子在运动过程中逐渐淡出的视觉效果。
准备工作
我们将创建两个缓冲区（或单个交错缓冲区），用于存储传递给顶点着色器的输入数据。
第一个缓冲区专门存储每个粒子的初始速度 —— 我们会从预设的有限向量范围内随机选取初始速度的数值。为了实现前文图片中粒子呈现的垂直 “锥形” 分布效果，我们会从锥形区域内的向量集合中随机选取（初始速度向量）。以下代码是实现该逻辑的一种方式：
vec3 v(0.0f);
float velocity, theta, phi;
GLfloat *data = new GLfloat[nParticles * 3];
for( GLuint i = 0; i<nParticles; i++ ) {
// 选取速度的方向
theta = glm::mix(0.0f, (float)PI / 6.0f, randFloat());
phi = glm::mix(0.0f, (float)TWOPI, randFloat());
v.x = sinf(theta) * cosf(phi);
v.y = cosf(theta);
v.z = sinf(theta) * sinf(phi);
// 缩放以设定速度的大小（速率）
velocity = glm::mix(1.25f,1.5f,randFloat());
v = v * velocity;
data[3*i] = v.x;
data[3*i+1] = v.y;
data[3*i+2] = v.z;
}
glBindBuffer(GL_ARRAY_BUFFER,initVel);
glBufferSubData(GL_ARRAY_BUFFER, 0,
nParticles * 3 * sizeof(float), data);
上述代码中，randFloat 函数会返回一个介于 0 到 1 之间的随机值。我们通过调用 GLM 库的 mix 函数，在预设的数值范围内选取随机数（GLM 的 mix 函数与 GLSL 中对应的函数功能完全一致：它会在第一个参数和第二个参数的数值之间执行线性插值）。在这里，我们先生成一个 0 到 1 之间的随机浮点数，再用这个值在目标数值区间的两个端点之间做插值，从而得到区间内的随机值。
为了从锥形区域内选取向量，我们采用球面坐标系来实现。其中，θ（theta）的值决定了锥形中心与锥体外边缘之间的夹角；而 φ（phi）的值则定义了在给定 θ 值的情况下，向量围绕 y 轴的所有可能方向。关于球面坐标系的更多细节，可参考该篇文章。
选定向量方向后，我们会对该向量进行缩放，使其模长（即速度大小）落在 1.25 到 1.5 之间。速度向量的模长对应粒子的整体运动速率，我们可以调整这个数值范围，来实现粒子运动速率的更多样化，或是让粒子整体运动得更快 / 更慢。
循环的最后三行代码将向量赋值到数组 data的对应位置。循环结束后，我们把数组数据拷贝到名为 initVel的缓冲区中，并将该缓冲区配置为顶点属性为0的输入数据源。
在第二个缓冲区中，我们将存储每个粒子的生成时刻（start time）。该缓冲区为每个顶点（即每个粒子）仅存储一个浮点型数值。在本示例中，我们会以固定速率依次创建每个粒子。以下代码将创建一个缓冲区，其中每个粒子的生成时间比前一个粒子晚 0.00075 秒：
float * data = new GLfloat[nParticles];
float time = 0.0f, rate = 0.00075f;
for( unsigned int i = 0; i<nParticles; i++ ) {
data[i] = time;
time += rate;
}
glBindBuffer(GL_ARRAY_BUFFER,startTime);
glBufferSubData(GL_ARRAY_BUFFER, 0,
nParticles * sizeof(float), data);
这段代码仅创建了一个浮点型数组：数组起始值为 0，每个元素依次递增 rate（步长）。随后该数组被拷贝到名为 startTime的缓冲区中，并将该缓冲区配置为顶点属性为1的输入数据源。
在 OpenGL 程序中设置以下统一变量（uniform）：
- ParticleTex：粒子所用的纹理
- Time：动画启动后流逝的总时长
- Gravity：表示前文运动方程中加速度一半的向量（对应公式中a/2 的部分）
- ParticleLifetime：粒子生成后的存活总时长
确保深度测试处于关闭状态，并通过以下语句启用 Alpha 混合：
glDisable(GL_DEPTH_TEST);
glEnable(GL_BLEND);
glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
还需要为每个点精灵设置合理的尺寸。例如，以下代码行将点精灵的尺寸设为 10 像素：
glPointSize(10.0f);
如何做
顶点着色器代码
#version 400
// 初始速度与生成时刻
layout (location = 0) in vec3 VertexInitVel;
layout (location = 1) in float StartTime;
out float Transp; // 粒子的透明度
uniform float Time; // 动画累计时间
uniform vec3 Gravity = vec3(0.0,-0.05,0.0); // 世界坐标系下的重力向量（对应a/2加速度）
uniform float ParticleLifetime; // 粒子最大存活时长
uniform mat4 MVP; // 模型视图投影矩阵
void main()
{
// 假定粒子初始位置为(0,0,0)
vec3 pos = vec3(0.0);
Transp = 0.0; // 初始透明度为0（不可见）
// 粒子在生成时刻前不显示
if( Time > StartTime ) {
float t = Time - StartTime; // 粒子的相对存活时长
// 若粒子未超过最大存活时长
if( t < ParticleLifetime ) {
// 计算粒子当前位置（位移公式：s = v0*t + 1/2*a*t²，Gravity已预存1/2*a）
pos = VertexInitVel * t + Gravity * t * t;
// 透明度线性衰减：存活越久，透明度越低
Transp = 1.0 - t / ParticleLifetime;
}
}
// 将粒子位置转换为裁剪坐标系下的坐标
gl_Position = MVP * vec4(pos, 1.0);
}
片元着色器代码
#version 400
in float Transp; // 从顶点着色器传入的粒子透明度
uniform sampler2D ParticleTex; // 粒子纹理采样器
layout ( location = 0 ) out vec4 FragColor; // 片元输出颜色
void main(){
// 采样粒子纹理（gl_PointCoord为点精灵的自动纹理坐标）
FragColor = texture(ParticleTex, gl_PointCoord);
// 将纹理的Alpha值与粒子透明度相乘，实现线性淡出
FragColor.a *= Transp;
}
工作原理
顶点着色器通过两个输入属性接收粒子的初始速度（VertexInitVel）和生成时刻（StartTime）。变量 Time 存储了从动画启动到当前所流逝的总时长，输出变量 Transp 则代表粒子的整体透明度。
在顶点着色器的 main 函数中，我们首先将粒子的初始位置设为模型坐标系原点 (0,0,0)，并将透明度初始化为 0.0（完全透明）。接下来的 if 语句会判断粒子是否已 “激活”：如果当前时间大于粒子的生成时刻，说明粒子已激活；反之，粒子仍未 “诞生”—— 这种情况下，粒子位置会保持在原点，且被渲染为完全透明的状态。
若粒子已激活，我们会用当前时间减去生成时刻，得到粒子的 “存活时长（age）” 并将其存入变量 t。如果 t 大于或等于粒子的最大存活时长（ParticleLifetime），说明粒子的动画周期已完全结束，此时粒子会被渲染为完全透明；反之，粒子仍处于活跃状态，我们会执行内层 if 语句的逻辑，完成粒子的动画驱动。
当粒子处于 “已激活且活跃” 状态时，其位置（pos）会通过前文所述的运动学方程计算得出。而粒子的透明度则会根据存活时长进行线性插值计算：
Transp = 1.0 – t / ParticleLifetime;
粒子诞生时完全不透明，随后会随着存活时长的增加线性变为透明 ——Transp 的值在粒子诞生时为 1.0（完全不透明），到存活周期结束时变为 0.0（完全透明）。
在片元着色器中，我们通过纹理采样的结果为片元上色。由于我们渲染的是 GL_POINT 图元，OpenGL 会自动计算纹理坐标，并将其存储在内置变量 gl_PointCoord 中供我们使用。最后，我们将最终颜色的 Alpha 值与 Transp 变量相乘，以此根据粒子的存活时长（由顶点着色器计算得出）来调整粒子的整体透明度。
更多
本示例旨在以相对易懂的方式介绍基于 GPU 的粒子系统。该系统的性能与灵活性尚有诸多可优化的空间，例如：我们可以让粒子的尺寸或旋转角度随其生命周期动态变化，以实现更多样的视觉效果。
我们也可以根据粒子与相机的距离调整其尺寸，以此更真实地体现远近透视效果。这一目标可通过两种方式实现：一是在顶点着色器中利用内置变量 gl_PointSize定义点尺寸；二是通过几何着色器将点精灵渲染为实际的四边形。
本节示例所用技术最显著的缺陷之一，是粒子难以被便捷地回收复用。当粒子 “消亡” 时，我们仅将其渲染为透明状态 —— 若能复用已消亡的粒子，就能营造出粒子持续不断喷射的视觉效果，这会大幅提升体验。此外，若能让粒子对变化的加速度或系统参数调整（例如风力变化、粒子发射源移动）做出实时响应，也会让效果更逼真。但基于前文所述的系统架构，我们无法实现这一点：因为当前粒子的运动由单一的运动学方程全程定义，而非基于当前受力情况增量更新位置（即物理模拟）。
要实现上述优化，我们需要一种方式，将顶点着色器的输出（粒子更新后的位置）反馈到下一帧顶点着色器的输入中。显然，若未在着色器内进行物理模拟，这件事会很简单 —— 只需在渲染前直接更新图元的位置即可。但由于我们的计算逻辑都在顶点着色器内完成，可写入内存的方式受到了严格限制。
在下一节示例中，我们将展示如何利用 OpenGL 的一项新特性 ——变换反馈（transform feedback） 来精准实现上述需求：我们可以指定特定的输出变量，将其写入缓冲区；这些缓冲区可在后续的渲染阶段被读取，作为顶点着色器的输入数据。
使用Transform Feedback创建粒子系统
变换反馈（Transform feedback）提供了一种将顶点（或几何）着色器的输出捕获到缓冲区的方式，以供后续渲染阶段使用。该特性最早随 OpenGL 3.0 版本引入，尤其适用于粒子系统 —— 核心原因是它支持我们实现离散模拟：我们可在顶点着色器内更新粒子位置，并在后续渲染阶段（或同一阶段）渲染该更新后的位置；而这些更新后的位置又能作为输入数据，用于下一帧动画的计算。
在本示例中，我们将实现与上一节《创建粒子喷泉》完全相同的粒子系统，但本次会采用变换反馈技术。我们不再使用单一方程描述粒子全程的运动规律，而是增量式更新粒子位置 —— 即每帧渲染时，基于当前时刻粒子所受的力求解运动方程，完成位置更新。
粒子模拟中一种常用的手段是欧拉方法（Euler method）：该方法会基于某一较早时刻粒子的位置、速度和加速度，近似计算出粒子在时刻 t 的位置与速度。
$$
\mathbf{P}_{n+1} = \mathbf{P}_n + \mathbf{v}n h \
\mathbf{v}{n+1} = \mathbf{v}_n + \mathbf{a}(t_n) h
$$
在上述方程中，下标代表时间步长（或动画帧）：P 表示粒子位置，v 表示粒子速度。这组方程将第 (n+1) 帧的粒子位置与速度，定义为前一帧（第 n 帧）位置和速度的函数。变量 h 代表时间步长（即相邻两帧之间流逝的时间）；函数 a(t_n) 表示瞬时加速度，该加速度基于粒子在时刻 (t_n) 的位置计算得出。在我们的模拟场景中，这个加速度会设为恒定值，但在通用场景下，它可能是一个随环境变化的动态值（例如受风力、碰撞、粒子间交互等因素影响）。
欧拉方法本质上是对牛顿运动方程进行数值积分的一种手段，也是实现该积分最简单的方法之一。但它属于一阶数值方法，这意味着该方法会引入显著的计算误差。精度更高的数值积分方法包括韦莱积分（Verlet integration）和龙格 - 库塔积分（Runge-Kutta integration）。不过由于我们的粒子模拟仅追求视觉效果的逼真性，对物理精度的要求并不高，因此欧拉方法已完全够用。
欧拉方法本质上是对牛顿运动方程进行数值积分的一种手段，也是实现该积分最简单的方法之一。但它属于一阶数值方法，这意味着该方法会引入显著的计算误差。精度更高的数值积分方法包括韦莱积分（Verlet integration）和龙格 - 库塔积分（Runge-Kutta integration）。不过由于我们的粒子模拟仅追求视觉效果的逼真性，对物理精度的要求并不高，因此欧拉方法已完全够用。
为了让我们的模拟系统能够正常运行，我们会采用一种被称作缓冲区 “乒乓操作（ping-ponging）” 的技术。我们维护两组顶点缓冲区，并在每一帧中互换它们的用途。例如，我们先将缓冲区 A 作为输入源，向顶点着色器提供粒子的位置与速度数据；顶点着色器通过欧拉方法更新这些位置和速度后，借助变换反馈（transform feedback）将更新结果写入缓冲区 B；随后，在第二遍渲染流程中，我们利用缓冲区 B 中的数据对粒子进行渲染。
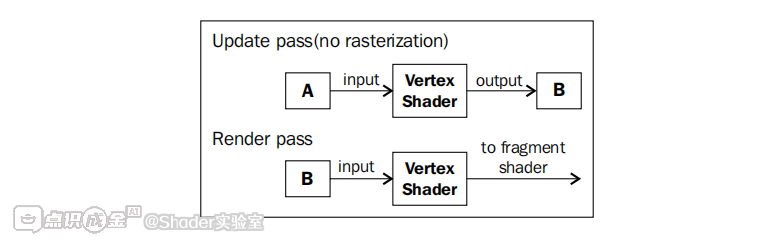
到下一帧动画时，我们会重复相同的流程，只是互换这两个缓冲区的角色。
总的来说，变换反馈机制允许我们定义一组着色器输出变量，并将这些变量的值写入指定的缓冲区（或一组缓冲区）。其实现涉及多个步骤（下文会逐一演示），核心思路如下：在着色器程序链接之前，我们通过 glTransformFeedbackVaryings函数定义缓冲区与着色器输出变量之间的关联关系；渲染阶段，我们启动一次变换反馈流程 —— 先将对应的缓冲区绑定到变换反馈绑定点（若有需要，可禁用光栅化，避免粒子被实际渲染）；接着调用 glBeginTransformFeedback函数启用变换反馈，随后绘制点图元，此时顶点着色器的输出会被存储到指定缓冲区中；最后调用 glEndTransformFeedback函数禁用变换反馈。
在本节示例的渲染流程中，我们会遵循以下步骤：
- 将粒子位置数据传入顶点着色器进行更新，并通过变换反馈捕获更新结果 —— 顶点着色器的输入数据来自缓冲区 A，输出结果则存储到缓冲区 B。此阶段我们会启用
GL_RASTERIZER_DISCARD标志，确保没有任何内容被实际渲染到帧缓冲区中。 - 以缓冲区 B 作为顶点着色器的输入，基于更新后的位置渲染粒子。
- 互换两个缓冲区的用途（为下一帧做准备）。
需注意的是，实际使用的是两组缓冲区（而非仅两个独立缓冲区）：每组缓冲区都包含对应各顶点属性的子缓冲区（如存储位置、速度、生成时刻的缓冲区）。
准备工作
创建并分配三对缓冲区：第一对用于存储粒子位置，第二对用于存储粒子速度，第三对用于存储每个粒子的 “生成时刻”（即粒子激活的时间点）。为便于区分，我们将每对中的第一个缓冲区称为 A 缓冲区，第二个称为 B 缓冲区。此外，我们还需要一个独立的缓冲区来存储每个粒子的初始速度。
创建两个顶点数组对象（VAO）：第一个顶点数组需将 A 位置缓冲区关联到第一个顶点属性（属性索引 0）、A 速度缓冲区关联到顶点属性 1、A 生成时刻缓冲区关联到顶点属性 2，同时将初始速度缓冲区关联到顶点属性 3；第二个顶点数组的配置逻辑完全相同，只是将 A 缓冲区替代为 B 缓冲区，初始速度缓冲区保持不变。在后续代码中，这两个顶点数组的句柄将通过名为 particleArray的 GLuint 类型数组访问。
为 A 缓冲区初始化合适的初始值：例如，将所有粒子的位置初始化为坐标原点，速度和生成时刻的初始化方式与上一节《创建粒子喷泉》中描述的一致；初始速度缓冲区可直接拷贝速度缓冲区的初始值。
使用变换反馈时，我们需要将缓冲区绑定到 GL_TRANSFORM_FEEDBACK_BUFFER目标下的索引化绑定点，以此指定接收顶点着色器输出数据的缓冲区 —— 绑定点的索引需与通过 glTransformFeedbackVaryings定义的顶点着色器输出变量索引一 一对应。
为简化操作，我们会使用变换反馈对象（Transform Feedback Object, TFO） 来管理缓冲区绑定关系。请使用以下代码为每组缓冲区创建两个变换反馈对象：
GLuint feedback[2]; // 变换反馈对象（TFO）数组，存储两个TFO句柄
GLuint posBuf[2]; // 位置缓冲区数组（posBuf[0]=A缓冲区，posBuf[1]=B缓冲区）
GLuint velBuf[2]; // 速度缓冲区数组（velBuf[0]=A缓冲区，velBuf[1]=B缓冲区）
GLuint startTime[2];// 生成时刻缓冲区数组（startTime[0]=A缓冲区，startTime[1]=B缓冲区）
// 创建并为posBuf、velBuf、startTime分配A/B两组缓冲区的显存空间
…
// 配置变换反馈对象
glGenTransformFeedbacks(2, feedback); // 生成2个变换反馈对象，句柄存入feedback数组
// 配置第一个变换反馈对象（feedback[0]）：关联A缓冲区组
glBindTransformFeedback(GL_TRANSFORM_FEEDBACK, feedback[0]);
// 将A位置缓冲区绑定到变换反馈绑定点0
glBindBufferBase(GL_TRANSFORM_FEEDBACK_BUFFER, 0, posBuf[0]);
// 将A速度缓冲区绑定到变换反馈绑定点1
glBindBufferBase(GL_TRANSFORM_FEEDBACK_BUFFER, 1, velBuf[0]);
// 将A生成时刻缓冲区绑定到变换反馈绑定点2
glBindBufferBase(GL_TRANSFORM_FEEDBACK_BUFFER, 2, startTime[0]);
// 配置第二个变换反馈对象（feedback[1]）：关联B缓冲区组
glBindTransformFeedback(GL_TRANSFORM_FEEDBACK, feedback[1]);
// 将B位置缓冲区绑定到变换反馈绑定点0
glBindBufferBase(GL_TRANSFORM_FEEDBACK_BUFFER, 0, posBuf[1]);
// 将B速度缓冲区绑定到变换反馈绑定点1
glBindBufferBase(GL_TRANSFORM_FEEDBACK_BUFFER, 1, velBuf[1]);
// 将B生成时刻缓冲区绑定到变换反馈绑定点2
glBindBufferBase(GL_TRANSFORM_FEEDBACK_BUFFER, 2, startTime[1]);
与顶点数组对象（VAO）类似，变换反馈对象（TFO）会存储 GL_TRANSFORM_FEEDBACK_BUFFER绑定点的缓冲区绑定关系，因此后续可快速重置这些绑定。在上述代码中，我们创建了两个变换反馈对象，并将它们的句柄存储在名为 feedback的数组中：对于第一个变换反馈对象，我们将 posBuf [0] 绑定到绑定点的索引 0、velBuf [0] 绑定到索引 1、startTime [0] 绑定到索引 2（即 A 缓冲区组）—— 每个 glBindBufferBase调用的最后一个参数都是对应缓冲区的句柄；对于第二个变换反馈对象，我们用 B 缓冲区组完成了完全相同的绑定操作。
完成上述配置后，我们只需绑定其中一个变换反馈对象，即可快速指定接收顶点着色器输出数据的缓冲区组。
需要设置的统一变量（Uniform）如下：
- ParticleTex：应用于点精灵的纹理
- Time：模拟总时长
- H：相邻两帧动画之间流逝的时间（时间步长）
- Accel：加速度
- ParticleLifetime：粒子被回收复用前的存活时长
如何做
顶点着色器代码
#version 400
// 定义子例程类型：无返回值、无参数的函数类型
subroutine void RenderPassType();
// 子例程统一变量：运行时动态指定调用update()或render()
subroutine uniform RenderPassType RenderPass;
// 输入顶点属性（与VAO绑定的缓冲区一一对应）
layout (location = 0) in vec3 VertexPosition; // 粒子当前位置（来自A/B缓冲区）
layout (location = 1) in vec3 VertexVelocity; // 粒子当前速度（来自A/B缓冲区）
layout (location = 2) in float VertexStartTime;// 粒子生成时刻（来自A/B缓冲区）
layout (location = 3) in vec3 VertexInitialVelocity; // 粒子初始速度（静态缓冲区，不参与乒乓）
// 变换反馈输出变量（会写入目标缓冲区）
out vec3 Position; // 更新后的粒子位置
out vec3 Velocity; // 更新后的粒子速度
out float StartTime;// 更新后的粒子生成时刻（回收时重置）
// 片元着色器输出变量（仅渲染通路使用）
out float Transp; // 粒子透明度
// 全局Uniform变量（CPU端传入，全着色器共享）
uniform float Time; // 模拟总时长（从系统启动到当前帧）
uniform float H; // 帧间时间步长（欧拉方法核心参数）
uniform vec3 Accel; // 粒子加速度（如重力vec3(0,-9.8,0)）
uniform float ParticleLifetime; // 粒子存活时长（到期后回收）
uniform mat4 MVP; // 模型视图投影矩阵（坐标转换用）
// 子例程1：更新通路（变换反馈阶段，仅计算粒子状态，不渲染）
subroutine (RenderPassType)
void update() {
// 初始化输出为当前输入（默认不修改粒子状态）
Position = VertexPosition;
Velocity = VertexVelocity;
StartTime = VertexStartTime;
// 仅处理已激活的粒子（当前时间≥生成时刻）
if( Time >= StartTime ) {
float age = Time - StartTime; // 粒子已存活时长
// 粒子超过存活阈值，执行回收复用
if( age > ParticleLifetime ) {
Position = vec3(0.0); // 位置重置为发射原点
Velocity = VertexInitialVelocity; // 速度恢复为初始随机速度
StartTime = Time; // 生成时刻重置为当前时间（重新激活）
} else {
// 粒子仍活跃，用欧拉方法增量更新状态
Position += Velocity * H; // 位置更新：pos = 上一帧pos + 上一帧vel × 时间步长
Velocity += Accel * H; // 速度更新：vel = 上一帧vel + 加速度 × 时间步长
}
}
}
// 子例程2：渲染通路（绘制阶段，仅计算渲染参数，不更新状态）
subroutine (RenderPassType)
void render() {
float age = Time - VertexStartTime; // 粒子存活时长
Transp = 1.0 - age / ParticleLifetime; // 透明度线性衰减（新生不透明，到期全透明）
// 将粒子世界坐标转换为裁剪坐标系，供光栅化使用
gl_Position = MVP * vec4(VertexPosition, 1.0);
}
void main()
{
// 根据子例程统一变量的配置，调用update()或render()
RenderPass();
}
片元着色器代码
#version 400
uniform sampler2D ParticleTex; // 粒子纹理采样器（绑定水滴/烟雾纹理）
in float Transp; // 从顶点着色器传入的粒子透明度
layout ( location = 0 ) out vec4 FragColor; // 片元最终输出颜色
void main()
{
// 采样粒子纹理（gl_PointCoord为点精灵自动生成的纹理坐标）
FragColor = texture(ParticleTex, gl_PointCoord);
// 将纹理自身Alpha与粒子生命周期透明度叠加，实现淡出效果
FragColor.a *= Transp;
}
步骤 1：着色器程序编译后、链接前 —— 配置变换反馈变量与缓冲区的映射
// 定义需要写入变换反馈缓冲区的顶点着色器输出变量名（顺序对应绑定点索引）
const char * outputNames[] = { "Position", "Velocity", "StartTime" };
// 配置变换反馈：建立着色器输出变量与缓冲区的关联关系
// 参数说明：
// progHandle → 着色器程序句柄（由glCreateProgram生成）
// 3 → 要关联的输出变量数量（Position/Velocity/StartTime）
// outputNames → 输出变量名数组（顺序对应变换反馈绑定点0/1/2）
// GL_SEPARATE_ATTRIBS → 每个变量写入独立缓冲区（而非交错存储在同一缓冲区）
glTransformFeedbackVaryings(progHandle, 3, outputNames, GL_SEPARATE_ATTRIBS);
步骤 2：渲染阶段 ——OpenGL 应用层核心代码（更新 + 渲染双通路）
/////////// 第一阶段：更新通路（仅计算粒子状态，不渲染）////////////
// 切换顶点着色器子例程为update()（执行粒子位置/速度更新逻辑）
glUniformSubroutinesuiv(GL_VERTEX_SHADER, 1, &updateSub);
// 设置更新通路所需的Uniform变量：帧间时间步长H、模拟总时长Time
…
// 禁用光栅化（跳过片元生成/渲染，仅执行顶点着色器计算，提升性能）
glEnable(GL_RASTERIZER_DISCARD);
// 绑定变换反馈对象（指定本次更新结果要写入的缓冲区组）
// drawBuf：当前“待渲染”缓冲区索引（0=A组，1=B组），feedback[drawBuf]对应写入目标
glBindTransformFeedback(GL_TRANSFORM_FEEDBACK, feedback[drawBuf]);
// 启动变换反馈（指定图元类型为GL_POINTS，与粒子渲染类型一致）
glBeginTransformFeedback(GL_POINTS);
// 绑定VAO：使用“非绘制缓冲区组”作为输入源（1-drawBuf实现乒乓切换）
glBindVertexArray(particleArray[1-drawBuf]);
// 绘制所有粒子：触发顶点着色器执行，更新后的状态写入变换反馈缓冲区
glDrawArrays(GL_POINTS, 0, nParticles);
// 结束变换反馈（停止向缓冲区写入数据）
glEndTransformFeedback();
// 启用光栅化（为后续渲染通路恢复光栅化功能）
glDisable(GL_RASTERIZER_DISCARD);
//////////// 第二阶段：渲染通路（基于更新后的状态绘制粒子）/////////////
// 切换顶点着色器子例程为render()（执行渲染参数计算逻辑，如透明度、裁剪坐标）
glUniformSubroutinesuiv(GL_VERTEX_SHADER, 1, &renderSub);
// 清空颜色缓冲区（避免上一帧画面残留）
glClear( GL_COLOR_BUFFER_BIT );
// 若需要，初始化变换矩阵相关Uniform（如MVP矩阵，用于坐标转换）
…
// 解绑变换反馈对象（渲染阶段无需向缓冲区写入，避免误操作）
glBindTransformFeedback(GL_TRANSFORM_FEEDBACK, 0);
// 绑定VAO：使用“更新后的缓冲区组”作为渲染输入源
glBindVertexArray(particleArray[drawBuf]);
// 绘制点精灵：基于更新后的粒子位置/透明度渲染到屏幕
glDrawArrays(GL_POINTS, 0, nParticles);
// 乒乓切换缓冲区索引：为下一帧交换“输入/输出”角色（0↔1）
drawBuf = 1 - drawBuf;
工作原理
这里有不少内容需要梳理清楚，我们先从顶点着色器说起。
顶点着色器被拆分为两个子例程函数：update 函数用于第一遍渲染流程（更新通路），它通过欧拉方法更新粒子的位置和速度；render 函数用于第二遍渲染流程（渲染通路），它根据粒子的存活时长计算透明度，并将位置和透明度传递给片元着色器。
顶点着色器定义了四个输出变量：前三个（Position、Velocity、StartTime）在第一遍流程中被写入变换反馈缓冲区；第四个变量（Transp）则在第二遍流程中作为片元着色器的输入。
update 函数的核心逻辑是：除非粒子尚未激活，或已超过其存活时长，否则都会通过欧拉方法更新粒子的位置和速度。如果粒子的存活时长超过了设定的生命周期，我们会对该粒子进行回收复用 —— 将其位置重置到坐标原点，把粒子的生成时刻更新为当前时间（Time 变量），并将其速度恢复为初始速度（通过输入属性 VertexInitialVelocity 传入）。
render 函数会计算粒子的存活时长，并据此确定粒子的透明度，将结果赋值给输出变量 Transp；同时，它会把粒子的位置转换为裁剪坐标系下的坐标，并将结果写入内置输出变量 gl_Position。
片元着色器仅在第二遍流程中生效，它仅根据粒子纹理 ParticleTex 和从顶点着色器传入的透明度（Transp）为片元上色。
着色器程序链接前的那段代码，作用是建立着色器输出变量与变换反馈缓冲区（绑定到 GL_TRANSFORM_FEEDBACK_BUFFER 绑定点索引的缓冲区）之间的对应关系。函数 glTransformFeedbackVaryings 接收三个核心参数：第一个是着色器程序对象的句柄；第二个是要关联的输出变量名称数量；第三个是输出变量名称数组 —— 数组中名称的顺序与变换反馈缓冲区的索引一一对应。在本例中，Position 对应索引 0，Velocity 对应索引 1，StartTime 对应索引 2。可以回顾前文创建变换反馈缓冲区对象的代码（glBindBufferBase 调用部分），验证这一索引对应关系是否一致。
glTransformFeedbackVaryings也可用于将数据发送到一个交错缓冲区（interleaved buffer） 中（而非为每个变量使用独立的缓冲区）。有关详细信息，请查阅 OpenGL 官方文档。
上面最后一段代码片段描述了如何在主 OpenGL 程序中实现渲染逻辑。在这个示例中，有两个重要的 GLuint 类型数组：feedback 和 particleArray。它们的大小均为 2，分别存储两个变换反馈缓冲区对象（TFO）和两个顶点数组对象（VAO）的句柄。变量 drawBuf 只是一个整数，用于在两组缓冲区之间来回切换 —— 在任意一帧中，drawBuf 的值要么是 0，要么是 1。
代码首先选择 update 子例程，以启用顶点着色器中的更新功能，随后设置 Uniform 变量 Time（模拟总时长）和 H（帧间时间步长）。接下来调用 glEnable(GL_RASTERIZER_DISCARD) 关闭光栅化，确保本阶段（更新通路）不会有任何内容被渲染。调用 glBindTransformFeedback 会选择与 drawBuf 对应的那一组缓冲区，作为变换反馈输出的目标缓冲区。
在绘制点图元（进而触发顶点着色器执行）之前，我们调用 glBeginTransformFeedback 启用变换反馈 —— 该函数的参数指定了要送入渲染管线的图元类型（本例中为 GL_POINTS）。从调用该函数到执行 glEndTransformFeedback 期间，顶点（或几何）着色器的输出都会写入绑定到 GL_TRANSFORM_FEEDBACK_BUFFER 绑定点的缓冲区中。在本例中，我们绑定与 1 - drawBuf 对应的顶点数组（若 drawBuf 为 0 则用 1，反之亦然）并绘制粒子。
更新通路结束时，我们通过 glDisable(GL_RASTERIZER_DISCARD) 重新启用光栅化，然后进入渲染通路。
渲染通路的逻辑十分简单：我们只需选择 render 子例程，然后从与 drawBuf 对应的顶点数组中读取数据并绘制粒子。为了安全起见，我们还会解绑变换反馈对象（将其绑定到索引 0）—— 这一步虽非严格必需，但由于同时对同一缓冲区进行读写通常不是明智之举，因此该操作是为了确保不会出现这种情况。
最后，在渲染结束时，我们通过将 drawBuf 设置为 1 - drawBuf 来完成缓冲区的乒乓切换。
更多
你可能会疑惑，为什么必须分两次渲染流程（双通路）来实现？我们为什么不能保持片元着色器处于激活状态，在同一通路中同时完成渲染和更新操作？对于本示例而言，单通路实现当然是可行的，而且效率还会更高。但我之所以选择以双通路的方式演示，是因为这大概率是实际开发中更通用的做法。粒子通常只是更大场景中的一小部分，而场景的绝大部分区域并不需要执行粒子更新逻辑。因此，在大多数真实的业务场景中，将粒子更新放在渲染通路之前单独执行是更合理的 —— 这样可以将粒子更新逻辑仅隔离在需要它的环节中，避免不必要的开销。
查询变换反馈结果
确定变换反馈过程中写入的图元数量往往十分实用。例如，若几何着色器处于激活状态，写入的图元数量可能与送入渲染管线的图元数量不一致。
OpenGL 提供了通过查询对象（query objects） 获取该信息的方式，具体步骤如下：
- 首先创建一个查询对象：
GLuint query;
glGenQueries(1, &query);
- 随后，在启动变换反馈流程前，通过以下命令开始计数：
glBeginQuery(GL_TRANSFORM_FEEDBACK_PRIMITIVES_WRITTEN, query);
- 变换反馈流程结束后，调用
glEndQuery停止计数：
glEndQuery(GL_TRANSFORM_FEEDBACK_PRIMITIVES_WRITTEN);
- 最后，通过以下代码获取写入的图元数量：
GLuint primWritten;
glGetQueryObjectuiv(query, GL_QUERY_RESULT, &primWritten);
printf("Primitives written: %d\n", primWritten);
粒子回收
在本示例中，我们通过重置粒子的位置和初始速度实现粒子回收。但这种方式会导致粒子随时间推移逐渐 “聚集” 在一起。若能为回收的粒子生成新的随机速度（甚至随机位置，具体取决于期望效果），视觉表现会更佳。
遗憾的是，着色器程序目前不支持原生的随机数生成功能。可行的解决方案包括：实现自定义随机数生成函数、使用存储随机值的纹理，或借助噪声纹理。
使用实例化的粒子创建一个粒子系统
为了给粒子系统中的每个粒子赋予更丰富的几何细节，我们可以利用 OpenGL 对实例化渲染（instanced rendering） 的支持。实例化渲染是一种便捷且高效的方式，用于绘制某个物体的多个副本。OpenGL 通过 glDrawArraysInstanced 和 glDrawElementsInstanced 两个函数提供实例化渲染能力。
在本示例中，我们会修改此前章节介绍的粒子系统：不再使用点精灵（point sprites），而是为每个粒子渲染更复杂的几何对象。下图展示了一个示例效果 —— 每个粒子被渲染为带光影效果的圆环（torus）：
使用实例化渲染的核心操作，只是调用其中一个实例化绘制函数并指定要绘制的实例数量。但向着色器传递顶点属性的方式存在一些细节需要注意：如果所有粒子都使用完全相同的属性绘制，操作会很简单，但视觉效果会毫无亮点（所有粒子会出现在同一位置、保持同一朝向）。由于我们希望为每个副本（粒子）绘制不同的位置，就需要找到一种方式，为每个粒子单独向顶点着色器传递所需信息（本例中为粒子的生成时刻）。
实现这一目标的关键是函数 glVertexAttribDivisor—— 该函数用于指定实例化渲染过程中顶点属性的步进频率。例如，考虑以下设置：
glVertexAttribDivisor(1, 1);
第一个参数是顶点属性索引，第二个参数表示 “属性值更新前要经过的实例数量”。换句话说，上述命令指定：
- 第一个实例的所有顶点，都会接收属性 1 对应的缓冲区中的第一个值；
- 第二个实例的所有顶点，接收该缓冲区中的第二个值，以此类推。
若第二个参数设为 2，则前两个实例接收第一个值、接下来两个实例接收第二个值，依此类推。
每个属性的默认除数（divisor）为 0，这意味着顶点属性会按常规方式处理（属性值每处理一个顶点步进一次，而非每处理若干个实例步进一次）。若某个属性的除数非 0，则称其为实例化属性（instanced attribute）。
准备工作
我们以《创建粒子喷泉》节中介绍的粒子系统为基础，仅对这个基础系统做少量修改。需注意的是，若有需要，你也可以将此方法与变换反馈结合使用；但为简化说明，我们将采用更基础的粒子系统 —— 将本示例适配到基于变换反馈的系统中也会非常直观。
在为粒子几何形状配置顶点数组对象（VAO）时，需新增两个用于初始速度和生成时刻的实例化属性。类似以下的代码即可实现该功能：
glBindVertexArray(myVArray);
// 配置属性0、1、2的指针（分别对应位置、法线、纹理坐标——几何体自身属性）
…
// 初始速度（属性3：实例化属性）
glBindBuffer(GL_ARRAY_BUFFER, initVel);
glVertexAttribPointer(3, 3, GL_FLOAT, GL_FALSE, 0, NULL);
glEnableVertexAttribArray(3);
glVertexAttribDivisor(3, 1); // 标记为实例化属性，每实例步进一次
// 生成时刻（属性4：实例化属性）
glBindBuffer(GL_ARRAY_BUFFER, startTime);
glVertexAttribPointer(4, 1, GL_FLOAT, GL_FALSE, 0, NULL);
glEnableVertexAttribArray(4);
glVertexAttribDivisor(4, 1); // 标记为实例化属性，每实例步进一次
// 若有需要，绑定元素数组缓冲区（EBO）
…
请注意上述代码中 glVertexAttribDivisor 的使用 —— 这表明属性 3 和属性 4 是实例化属性（数组中的值仅会在每处理一个实例时步进一次，而非每处理一个顶点步进一次）。因此，这两个属性对应的缓冲区大小必须与实例数量（粒子数） 成正比，而非与单个实例的顶点数成正比。而属性 0、1、2 对应的缓冲区（几何体属性）则需像往常一样，按单个实例的顶点数来确定大小。
顶点属性除数（vertex attribute divisor）的值会成为顶点数组对象（VAO）状态的一部分 —— 因此，与 VAO 状态中的其他元素（如顶点属性指针、属性启用状态等）一样，我们只需在后续绑定该 VAO，即可重置（恢复）这个除数配置。
如何做
顶点着色器的代码与此前《创建粒子喷泉》章节中展示的代码几乎完全一致，差异仅体现在输入、输出变量上。可使用类似以下的代码：
layout (location = 0) in vec3 VertexPosition; // 几何体顶点位置（每个顶点不同）
layout (location = 1) in vec3 VertexNormal; // 几何体顶点法线（每个顶点不同）
layout (location = 2) in vec3 VertexTexCoord; // 几何体纹理坐标（每个顶点不同）
layout (location = 3) in vec3 VertexInitialVelocity; // 粒子初始速度（每个实例/粒子不同）
layout (location = 4) in float StartTime; // 粒子生成时刻（每个实例/粒子不同）
out vec3 Position; // 传递给片元着色器的粒子位置（相机坐标系）
out vec3 Normal; // 传递给片元着色器的法线（相机坐标系）
在主函数中，需利用运动方程平移顶点位置，以此更新粒子的位置：
Position = VertexPosition + VertexInitialVelocity * t + Gravity * t * t;
务必将法线（经坐标转换后）和更新后的位置（相机坐标系下）传递给片元着色器。
在片元着色器中，实现你偏好的着色模型即可（比如冯氏 / Phong 着色模型？）。
在主 OpenGL 程序的渲染函数中，使用以下代码渲染实例（粒子）：
glBindVertexArray(myVArray); // 绑定配置好的VAO（自动恢复实例化属性除数等状态）
glDrawElementsInstanced(
GL_TRIANGLES, // 图元类型（与几何体的索引数据匹配）
nEls, // 单个实例的索引数量（如圆环的三角面索引总数）
GL_UNSIGNED_INT, // 索引数据类型
0, // 索引缓冲区的偏移量（从起始位置读取）
nParticles // 实例数量（粒子总数）
);
工作原理
回顾一下，顶点着色器的前三个输入属性属于非实例化属性—— 也就是说，它们每处理一个顶点就会步进一次（数值更新），且在每个实例中会重复遍历其完整的顶点数据；最后两个属性（属性 3 和 4）是实例化属性，仅会在每处理一个实例时更新一次。因此，最终的效果是：每个实例（粒子）都会根据运动方程的计算结果整体平移。
glDrawElementsInstanced 函数会绘制该物体的 nParticles 个实例。当然，nEls 指的是每个实例包含的索引数量（注：原文 “number of vertices” 为笔误，该函数第二个参数是索引数而非顶点数）。
更多
OpenGL 为顶点着色器提供了一个名为 gl_InstanceID 的内置变量。它本质上是一个计数器，会为每个被渲染的实例分配唯一的数值 —— 第一个实例的 ID 为 0，第二个为 1，依此类推。这个变量十分实用：既可以作为索引，为每个实例调取适配的纹理数据；也可以利用实例 ID 为该实例生成专属的随机数据。例如，我们可以将实例 ID（或其哈希值）作为伪随机数生成函数的种子，为每个实例生成唯一的随机序列。
粒子模拟火焰
要实现大致模拟火焰的效果，我们只需对基础粒子系统做几处修改即可。由于火焰这种物质受重力的影响极小，因此我们无需考虑向下的重力加速度；事实上，我们反而会采用轻微的向上加速度，让粒子在火焰顶端附近散开。同时，我们还会分散粒子的初始位置，避免火焰的底部仅局限于单个点。当然，我们需要使用带有火焰标志性红、橙色系的粒子纹理。
下图展示了该粒子系统运行时的效果示例：
用于粒子的纹理呈现出火焰色系的浅淡 “晕染 / 模糊效果”（smudge）。由于在印刷品中该纹理的可视效果极差，因此此处未展示该纹理。
准备工作
以《使用变换反馈创建粒子系统》章节中介绍的基础粒子系统为起点，按以下步骤调整以实现火焰效果：
- 将统一变量（uniform）
Accel设置为一个较小的向上数值，例如(0.0, 0.1, 0.0)； - 将统一变量
ParticleLifetime（粒子生命周期）设置为约 4 秒； - 为粒子创建并加载带有火焰色系的纹理，将其绑定到第一个纹理单元，并将统一变量
ParticleTex设为 0； - 将点大小（point size）设置为约 50.0。
如何做
在为粒子设置初始位置时，不要将所有粒子都置于原点，而是为其分配随机的 x 坐标。可使用如下代码实现：
GLfloat *data = new GLfloat[nParticles * 3];
for( int i = 0; i < nParticles * 3; i += 3 ) {
data[i] = glm::mix(-2.0f, 2.0f, randFloat()); // x坐标随机（-2.0~2.0）
data[i+1] = 0.0f; // y坐标固定为0（火焰底部）
data[i+2] = 0.0f; // z坐标固定为0
}
glBindBuffer(GL_ARRAY_BUFFER, posBuf[0]); // posBuf[0]为变换反馈的位置缓冲区（A组）
glBufferSubData(GL_ARRAY_BUFFER, 0, size, data); // 将初始位置写入缓冲区
在设置初始速度时，我们要确保 x 和 z 分量为 0，仅让 y 分量包含随机速度。结合此前选定的向上加速度（见前文代码），这会让每个粒子仅沿 y 轴（垂直方向）运动：
// 为第一个速度缓冲区填充随机速度
for( unsigned int i = 0; i < nParticles; i++ ) {
data[3*i] = 0.0f; // x方向速度为0
data[3*i+1] = glm::mix(0.1f, 0.5f, randFloat()); // y方向随机速度（0.1~0.5）
data[3*i+2] = 0.0f; // z方向速度为0
}
glBindBuffer(GL_ARRAY_BUFFER, velBuf[0]); // velBuf[0]为变换反馈的速度缓冲区（A组）
glBufferSubData(GL_ARRAY_BUFFER, 0, size, data);
glBindBuffer(GL_ARRAY_BUFFER, initVel); // initVel为初始速度缓冲区（供回收时复用）
glBufferSubData(GL_ARRAY_BUFFER, 0, size, data);
在顶点着色器中回收粒子时，重置 y 和 z 坐标，但保留 x 坐标不变：
…
if( age > ParticleLifetime ) {
// 粒子超过生命周期，执行回收
Position = vec3(VertexPosition.x, 0.0, 0.0); // 保留原x坐标，y/z重置为0
Velocity = VertexInitialVelocity; // 复用初始速度
StartTime = Time; // 重置生成时刻
} else {
…
工作原理
我们将所有粒子初始位置的 x 坐标随机分布在 - 2.0 到 2.0 之间，并将初始速度的 y 坐标设为 0.1 到 0.5 之间的随机值。由于加速度仅包含 y 分量，粒子将仅沿 y 方向的笔直垂直线运动。位置的 x 或 z 分量应始终保持为 0（注：此处 x 分量描述为笔误，实际 x 分量保留初始随机值，仅 z 分量恒为 0）。如此一来，在回收粒子时，我们只需将 y 坐标重置为 0，即可让粒子在其初始位置重新开始运动。
更多
当然，如果你想实现向不同方向飘动（比如被风吹动）的火焰效果，就需要为加速度设置不同的取值（即加入 x/z 分量）。这种情况下，我们此前将粒子重置到初始位置的小技巧（仅重置 y 坐标）就不再奏效了。不过解决方案也很简单：只需在粒子系统中新增一个缓冲区（与存储初始速度的缓冲区类似），专门保存每个粒子的初始位置，并在回收粒子时复用这个初始位置即可。
粒子模拟烟雾
烟雾的特征是大量微小颗粒从源头飘散开，且在空气中运动的过程中逐渐扩散。我们可以通过为粒子设置较小的向上加速度（或恒定向上速度）来模拟这种漂浮效果，但要逐个模拟每个微小烟雾颗粒的扩散行为，开销会过于高昂。因此，我们换一种思路：让模拟烟雾的粒子随时间逐渐变大（尺寸增长），以此来等效模拟大量微小颗粒的扩散效果。
下图展示了该模拟方案的效果示例：
每个粒子所用的纹理呈现出极浅的灰色或黑色晕染 / 模糊效果（light smudge）。
要实现粒子随时间逐渐变大的效果，我们会用到 OpenGL 的 GL_PROGRAM_POINT_SIZE 功能 —— 该功能允许我们在顶点着色器内修改点精灵的尺寸（point size）。
准备工作
以《使用变换反馈创建粒子系统》章节中介绍的基础粒子系统为起点，完成以下配置：
- 将统一变量（uniform）
Accel设置为较小的向上数值，例如(0.0, 0.1, 0.0)； - 将统一变量
ParticleLifetime（粒子生命周期）设置为约 6 秒； - 为粒子创建并加载浅灰色模糊晕染风格的纹理，将其绑定到第一个纹理单元，并将统一变量
ParticleTex设为 0； - 将统一变量
MinParticleSize（最小粒子尺寸）和MaxParticleSize（最大粒子尺寸）分别设为 10 和 200。
实现步骤
- 将粒子的初始位置设为原点；按《使用变换反馈创建粒子系统》中描述的方式定义初始速度，但需注意：将 theta 角（极角 / 方位角）设置为大方差（large variance） 时效果最佳（让初始速度方向更分散）；
- 在顶点着色器中新增以下统一变量：
uniform float MinParticleSize;
uniform float MaxParticleSize;
- 同样在顶点着色器中，为渲染子例程（render）编写如下代码：
subroutine (RenderPassType)
void render() {
float age = Time - VertexStartTime; // 粒子已存活时长
Transp = 0.0; // 透明度（输出到片元着色器）
if( Time >= VertexStartTime ) { // 粒子已激活（未到生成时刻则不渲染）
float agePct = age / ParticleLifetime; // 生命周期占比（0.0~1.0）
Transp = 1.0 - agePct; // 透明度随生命周期降低（1.0→0.0）
// 按生命周期占比，从最小尺寸线性插值到最大尺寸
gl_PointSize = mix(MinParticleSize, MaxParticleSize, agePct);
}
// 粒子最终裁剪坐标
gl_Position = MVP * vec4(VertexPosition, 1.0);
}
在主 OpenGL 应用程序中，渲染粒子之前，务必启用 GL_PROGRAM_POINT_SIZE 功能：
glEnable(GL_PROGRAM_POINT_SIZE);
工作原理
渲染子例程函数会将内置变量 gl_PointSize 设置为一个介于 MinParticleSize（最小粒子尺寸）和 MaxParticleSize（最大粒子尺寸）之间的值 —— 该值由粒子的 “存活时长（age）” 决定。这一机制使得粒子在系统中运动的过程中，尺寸会随时间逐渐增大。
需注意：除非启用了 GL_PROGRAM_POINT_SIZE，否则 OpenGL 会完全忽略 gl_PointSize 变量的取值。
