本教程将教你如何掌握3D逆向运动学：这项技术解决了如何移动机械臂以达到特定目标的问题。
你可以在这里阅读本在线课程的其余部分:
引言
逆向运动学不仅是在电子游戏中会反复出现，在工程和科学领域也同样普遍。从机械臂的设计到对人类大脑对运动控制的理解，逆向运动学——无论以何种形式都扮演着重要的角色。
本系列的机械臂适用于前后两臂相连的情况，通过简单的三角函数相关算法实现更高的性能(后面将讨论适用于更多关节的机械臂实现，但是性能相比会较低)。
向三维空间扩展
如果你之前关注过《2D逆向运动学》系列，那么前面的内容对你来说应该并不陌生。如果你没有看过，建议回头看看。
之前我们做了个简化的2D机械臂案例，它可以作为解决3D逆向运动学的起点。
首先，我们需要理解，2D中的双关节机械臂具有两个自由度（2DOF）。与人们的想象相反，这并不意味着我们有两段机械臂；而是我们能够控制两个变量（即关节角度）。
当我们将这个问题扩展到三维空间时，我们的机械臂仍然有两段和两个关节。然而，如果我们假设我们还可以围绕第一个关节自由旋转机械臂，那么问题现在具有三个自由度（3DOF）。
在这种新场景下，第二个关节（B）保持不变。然而，我们假设第一个关节（A）现在可以在另一个维度上自由旋转。因此，第一个关节通常被称为“髋关节”，第二个关节被称为“膝关节”。你的膝关节通常只有一个自由度（前后），而髋关节有两个自由度（前后和内外）。髋关节旋转的角度用θ表示。
我们可以想象一个机械臂，其中两个关节都有两个自由度，总共四个自由度。但问题在于，这将导致存在多个解，使我们的方法不再有效。但是“腿式”机械臂（即具有髋关节和膝关节的机械臂）在游戏和工业中都非常常见。所以这种方法很值得研究。
如果你读过之前的文章，你可能会记得，如果目标在2D中是可“触及”的，那么总是存在两个“镜像”解（如下所示）。
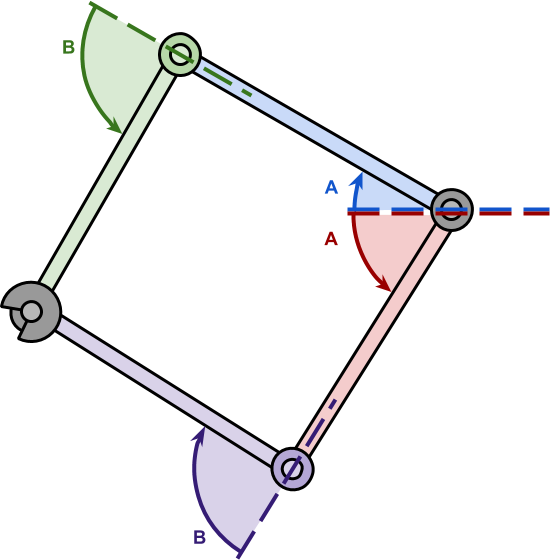
从2D到3D
到目前为止，我们只知道如何解决运动区域被限制在XY平面内的逆向运动学问题。从2D到3D的维度扩展也需要使用2D的解决方案。下方的动画展示了一个机械臂在3D空间中试图到达一个围绕Y轴旋转的点。很明显，机械臂唯一做的也是旋转；它的角度A和B没有变化，只有θ在变化。
这意味着，如果我们知道在XY平面上执行逆向运动学（前面已经讲过），那么我们就可以通过两次简单的旋转在整个XYZ空间中执行。从概念上讲，我们可以通过三个步骤来解决这个问题：
- 将目标点围绕Y轴旋转，直到它位于XY平面上。
- 移动机械臂，使其能够像在2D中一样到达目标点。
- 通过围绕Y轴反向旋转整个机械臂来“撤销”之前的旋转。
我们可以通过更高效的方式实现这一点，即不在XY平面上执行2D逆向运动学，而是在从机械臂根部到目标点的垂直平面上执行。
围绕Y轴旋转
要在3D中运用逆向运动学，我们首先需要计算θ，这是整个机械臂旋转的角度。这是添加到髋关节的额外自由度。
找到θ的最佳方法是假设机械臂已经到达目标位置（即C已经位于目标点），然后计算得到的角度θ。由于θ是髋关节围绕Y轴旋转的角度，我们可以直接从顶部观察机械臂。在XZ平面的俯视图中（如下所示），机械臂看起来像一条直线。这是因为，除了髋关节外，其他两个关节都被限制在一个平面上。
如果我们将线段AC视为一个直角三角形的斜边，我们可以使用一些三角函数来计算角度θ：
$$
θ=tan^{-1}({Δz \over Δx})=tan^{-1}({Cz-Az \over Cx-Ax})
$$
在WY平面上进行逆向运动学
从技术上讲，知道θ已经足以解决3D逆向运动学问题。事实上，我们可以按照上面提出的算法：将目标点围绕Y轴旋转-θ角度，在XY平面上执行逆向运动学，最后将整个机械臂旋转+θ角度。
更快的版本是，不在2D平面上执行逆向运动学，而是直接在通过髋关节和目标点的垂直平面上执行。然而，不幸的是，有一些因素阻止我们这样做。让我们再次查看标有所有角度的示意图：
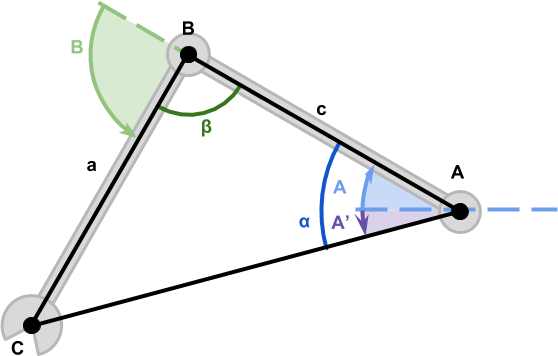
为了计算控制第一个关节的角度A，我们需要计算A'。这是第一个关节与目标点之间的角度。如果我们回顾用于计算A'的方程，我们会注意到一个大问题：它假设所有点都位于XY平面上：
在我们的3D场景中，机械臂是会围绕Y轴旋转θ角度的。然而，如果我们连同机械臂一起旋转对应角度，新的示意图可以基本维持不变。我们将这个新的参考系称为WY，因为X轴现在被W轴取代，W轴是未围绕Y轴旋转θ角的X轴。
我们不能像计算Δy那样简单地使用Dx - Ax。这是因为虽然C和D在Y轴上对齐，但A和D并不与X轴对齐。它们与W轴对齐。因此，计算Δw的最佳方法是获取A到D的距离。这会丢失Δw的符号，但幸运的是，这对我们的计算没有实际影响。如果你的机械臂向相反方向移动，只需在代码中翻转Δw的符号即可。
其中$\left|\overline{A D}\right|$是从A到D的线段长度。可以通过诸如 Vector3.Distance的函数轻松计算，或者你也可以直接使用勾股定理：
在上面的方程中，勾股定理中的Y分量被抵消了，因为点D的Y分量与A相同，所以它们的Δy为零。
现在，我们确实拥有了所有必要的工具，来为具有一个膝关节和髋关节的机械臂在3D中执行逆向运动学：
