我们讨论的是Dot3 bump mapping贴图,它也叫NormalMap,是目前图形硬件模拟凹凸效果比较通用的方法,所以下文中的凹凸贴图通指Dot3 bump mapping(NormalMap)
Phong反射模型使用面法线来计算漫反射和高光。但是实际上表面很少是完全平坦的,为了增加我们的渲染真实感,则必须找到一种方法来模拟表面的粗糙度。本篇将介绍凹凸贴图,一种存储表面粗糙度的方法,以及如何在我们的照明着色器中使用凹凸贴图。
Bump Maps
之前文章中提到,即使在Phong着色中,表面法线信息也必须通过顶点的插值来确定。虽然这将为每个片元创建一个独特的法线,但法线仍然不能准确地表示表面的粗糙程度。以砖墙为例,我们可以使用四边形来模拟砖墙,从而产生单个法线(无论是否共用顶点)。但是砖墙不是平坦的,而是由许多微表面组成——水泥等都可能造成砖的表面变得相当粗糙。那么,如何准确地模拟一个表面的粗糙度呢?有一个方法是:可以使用足够的多边形来细分表面,但这样的解决方案在计算上会造成一些性能问题。更好的解决方案是使用凹凸贴图。就像我们目前使用的纹理贴图来模拟表面的颜色一样,凹凸贴图模拟它的粗糙度。凹凸贴图不是逐片元对应一种颜色,而是逐片元对应一条法线,每条法线根据它们所模拟的凹凸程度来指向不同的方向。

左图是表面法线,右图为根据凹凸贴图生成的面法线
凹凸贴图通常保存为普通的RGB纹理,纹理中的每个通道分别存储标准化方向向量的x、y、z轴的值。由于凹凸贴图是颜色数据,就像使用其他纹理一样,可以对采样数据进行插值,无论凹凸贴图的分辨率多大,都会插值并产生对应的逐片元法线。

普通纹理+凹凸贴图=纹理逐片元照明结果
Tangents
凹凸贴图是在切线空间中定义它们的法线。为了在照明计算中使用它们,它们必须转换到其他空间,如世界空间。
我们不能仅仅通过面法线或顶点法线来转换凹凸贴图——法线可以看成一个轴,而一个轴有无限多个方向。为了将切线空间法线完全转换为世界空间,我们需要3个轴,形成一个旋转矩阵。面法线是其中一个轴,那么另外两个轴是什么呢?因为法线垂直于曲面,所以我们需要的另一个方向很容易得知,它不是沿着目标多边形的面就是与目标多边形曲面相切。只剩下最后一个轴,这个轴被称为副法线(Binormal)(也有些教程叫副切线(Bitangent)),可以通过取法向量和切向量的叉积来计算。
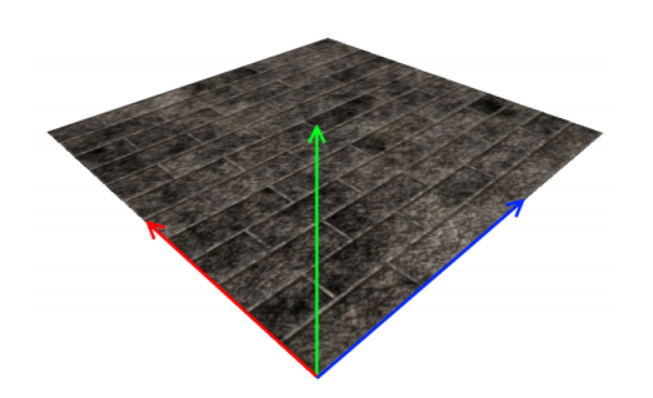
绿轴为法线,蓝轴为切线,红轴为副法线
在法线那篇文章中说到,可通过顶点与顶点间的向量(c-a与b-a)通过叉积,来求取法向量。这种方式确实能正确求取法向量,但是切向量与副法线的求取是不是也能通过这种方式求取呢?(毕竟一个平面也有无数条的切向量),这好像行不通,简单的以正方形举例,正方形由两个三角形组成,但是最终会产生互相冲突的切向量/副法线。
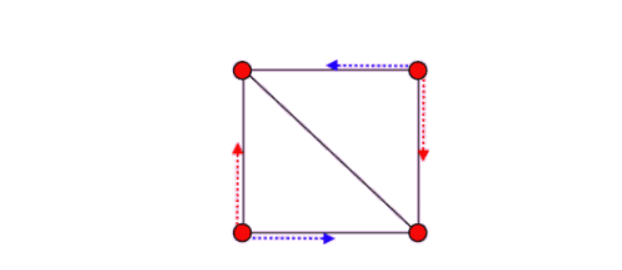
蓝轴为切向量,红轴为副法线
为了让切向量/副法线向量在相应顶点中指向的方向完全一致,我们使用模型纹理坐标的正x轴方向作为切线方向。只要纹理坐标的方向不变,就可以保持切向量的一致性,从而保证副法线的一致性。
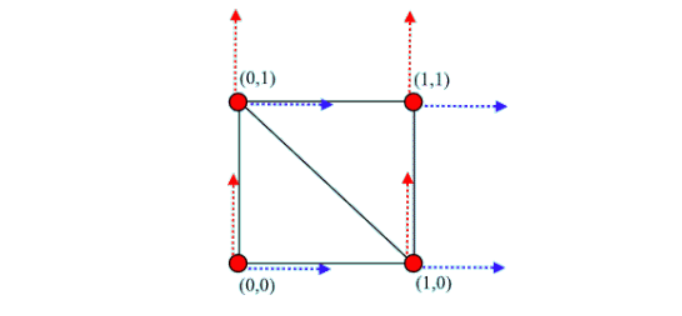
Tangent space to World space
为了从切线空间到世界空间的转换,标准化后的切向量、副法线和法向量被组合成一个"Tangent Binormal Normal"的旋转矩阵(TBN矩阵),如下所示:
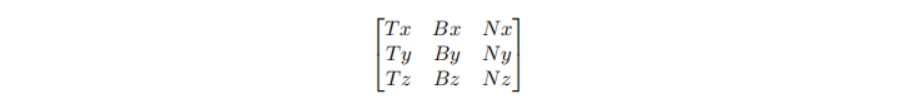
根据法线与切向量就可以求取出副法线向量:
最后将凹凸贴图法线乘以TBN矩阵,将它从切线空间转换到世界空间,在世界空间中的凹凸贴图法线就可以用来执行光照计算了。
Example Program
void Mesh::GenerateTangents()
{
if (!tangents) {
tangents = new Vector3[numVertices];
}
if (!textureCoords) {
return; // Can ’t use tex coords if there aren ’t any !
}
for (GLuint i = 0; i < numVertices; ++i) {
tangents[i] = Vector3();
}
// 共用顶点
if (indices) {
for (GLuint i = 0; i < numIndices; i += 3) {
int a = indices[i];
int b = indices[i + 1];
int c = indices[i + 2];
Vector3 tangent = GenerateTangent(vertices[a], vertices[b],
vertices[c], textureCoords[a],
textureCoords[b], textureCoords[c]);
tangents[a] += tangent;
tangents[b] += tangent;
tangents[c] += tangent;
}
}
// 非共用顶点
else {
for (GLuint i = 0; i < numVertices; i += 3) {
Vector3 tangent = GenerateTangent(vertices[i], vertices[i + 1],
vertices[i + 2], textureCoords[i],
textureCoords[i + 1], textureCoords[i + 2]);
tangents[i] += tangent;
tangents[i + 1] += tangent;
tangents[i + 2] += tangent;
}
}
for (GLuint i = 0; i < numVertices; ++i) {
tangents[i].Normalise();
}
}
Vector3 Mesh::GenerateTangent(const Vector3& a, const Vector3& b, const Vector3& c, const Vector2& ta, const Vector2& tb, const Vector2& tc)
{
Vector2 coord1 = tb - ta;
Vector2 coord2 = tc - ta;
Vector3 vertex1 = b - a;
Vector3 vertex2 = c - a;
Vector3 axis = Vector3(vertex1 * coord2.y - vertex2 * coord1.y);
float factor = 1.0f / (coord1.x * coord2.y - coord2.x * coord1.y);
return Vector3.normalize(axis * factor);
}
GenerateTangents函数生成切线的原理与生成法线的原理类似,当有索引缓冲区使顶点共用时,需要对与该顶点相关面的切线标准化后叠加。重点理解下GenerateTangent函数。
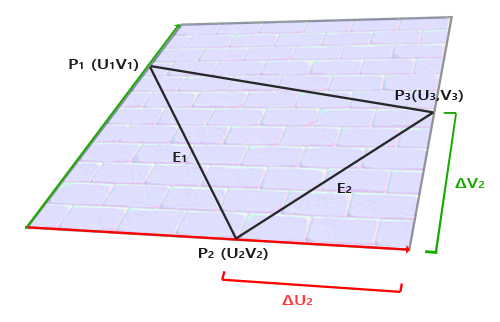
上图中E2是(P3-P2)向量,E1是(P1- P2)向量,ΔU2与ΔV2是顶点P3与P2位置对应的UV坐标差,而ΔU2在切线方向上,ΔV2在副法线方向上,所以结合E1与E2可得到下面公式(公式中ΔU1与ΔV1则是顶点P1与P2位置对应的UV坐标差):
展开为:
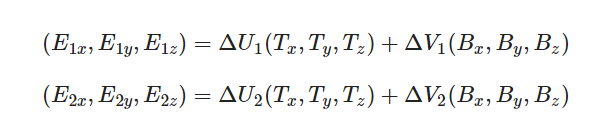
添加图片注释,不超过 140 字(可选)
可看成矩阵乘法,继续展开:
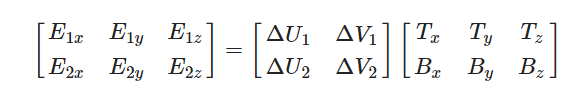
添加图片注释,不超过 140 字(可选)
剩下的就是解T与B,可以使左右两边同时左乘于下述矩阵的逆矩阵:
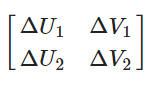
添加图片注释,不超过 140 字(可选)
可得:
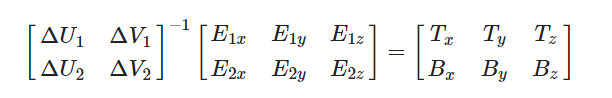
添加图片注释,不超过 140 字(可选)
逆矩阵可以展开为,1除以原矩阵的行列式,再乘以它的伴随矩阵:
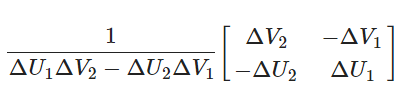
添加图片注释,不超过 140 字(可选)
得到:
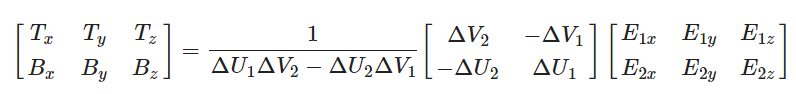
添加图片注释,不超过 140 字(可选)
有了上述公式后就可以得到切线与副法线了,但是由于开发过程中不会在顶点着色器中定义副法线,所以我们在C++代码中只求取了切线向量,副法线在着色器中计算。
下面是着色器代码:
uniform mat4 modelMatrix;
uniform mat4 viewMatrix;
uniform mat4 projMatrix;
uniform mat4 textureMatrix;
in vec3 position;
in vec4 colour;
in vec3 normal;
// 切线
in vec3 tangent;
in vec2 texCoord;
out Vertex {
vec4 colour;
vec2 texCoord;
vec3 normal;
// 切线
vec3 tangent;
// 副法线
vec3 binormal;
vec3 worldPos;
} OUT;
void main() {
OUT.colour = colour;
OUT.texCoord = (textureMatrix * vec4(texCoord, 0.0f, 1.0f)).xy;
mat3 normalMatrix = transpose(inverse(mat3(modelMatrix)));
OUT.normal = normalize(normalMatrix * normalize(normal));
OUT.tangent = normalize(normalMatrix * normalize(tangent));
OUT.binormal = normalize(normalMatrix * normalize(cross(normal, tangent)));
OUT.worldPos = (modelMatrix * vec4(position, 1.0f)).xyz;
gl_Position = (projMatrix * viewMatrix * modelMatrix) * vec4(position, 1.0f);
}
在顶点着色器中已经求取世界空间中的T,B,N向量了,所以在片元着色器中通过他们建立TBN矩阵,使凹凸贴图中的法线变换到世界空间中。
uniform sampler2D diffuseTex;
uniform sampler2D bumpTex; // 凹凸贴图
uniform vec3 cameraPos;
uniform vec4 lightColour;
uniform vec3 lightPos;
uniform float lightRadius;
in Vertex {
vec4 colour;
vec2 texCoord;
vec3 normal;
// 切线
vec3 tangent;
// 副法线
vec3 binormal;
vec3 worldPos;
}IN;
out vec4 fragColour;
void main () {
vec4 diffuse = texture(diffuseTex, IN.texCoord);
// TBN矩阵
mat3 TBN = mat3(IN.tangent, IN.binormal, IN.normal);
// 转换凹凸贴图中的法线向量至世界空间中
vec3 normal = normalize(TBN * (texture(bumpTex,
IN.texCoord).rgb * 2.0 - 1.0));
vec3 incident = normalize(lightPos - IN.worldPos);
float lambert = max(0.0, dot(incident, normal)); // Different !
float dist = length(lightPos - IN.worldPos);
float atten = 1.0 - clamp(dist/lightRadius, 0.0, 1.0);
vec3 viewDir = normalize(cameraPos - IN.worldPos);
vec3 halfDir = normalize(incident + viewDir);
float rFactor = max(0.0, dot(halfDir, normal)); // Different !
float sFactor = pow(rFactor, 33.0);
vec3 colour = (diffuse.rgb * lightColour.rgb);
colour += (lightColour.rgb * sFactor) * 0.33;
fragColour = vec4(colour * atten * lambert, diffuse.a);
fragColour.rgb += (diffuse.rgb * lightColour.rgb) * 0.1;
}
上述是转换凹凸贴图至世界空间中运算的一种方式,还有另一种方法是把所有的计算都放在切线空间中,这种方式需要把光线向量与视图向量转换到切线空间中,转换的方式也很简单,把视图向量/入射向量乘上TBN矩阵的逆矩阵(转置矩阵)即可完成转换,这种方式往往效率更高,因为视图向量/入射向量在顶点着色器中进行转换即可,相比片元着色器中进行凹凸贴图法线要进行逐片元的转换相比,效率必然更高。
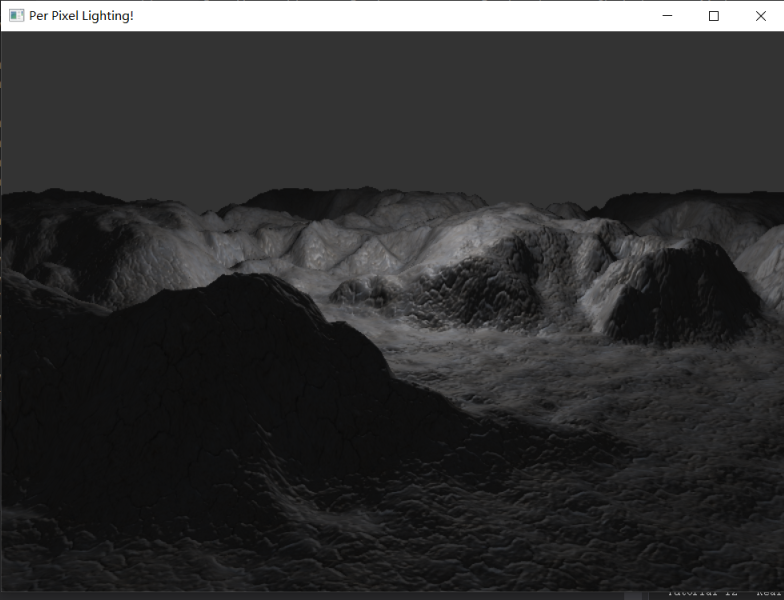
运行后的输出结果如下: