Normals
为了模拟光线在模型表面上的反射效果,我们必须确定模型表面所面对的方向,而法线就能够确定该方向的指向。这是一个标准化的方向向量,指向的方向远离模型的表面:
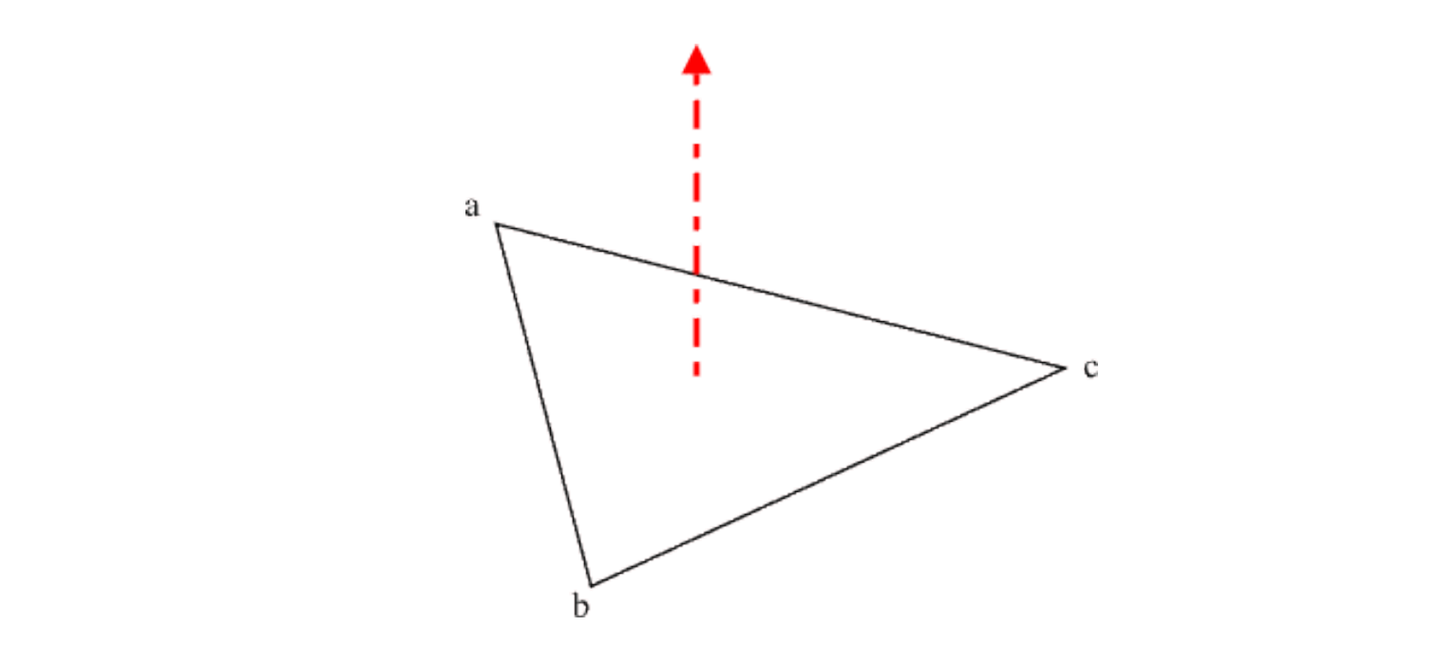
三角形每个顶点附带的法线信息称为顶点法线(vertex normal),通过顶点间向量的叉乘求取的法线称为面法线(face normal)。
Calculating Normals
所有在屏幕上渲染的几何图形都是由三角形组成的,幸运的是,计算三角形的表面法线非常容易。两个向量a和b,它们的叉积结果可以得到一个与向量a与b同时正交的向量,该向量即为面法线(face normal)。
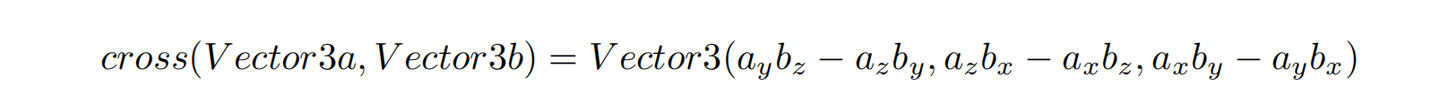
但是要取哪两个向量作为叉积来求取正确的法线向量呢?简单,我们选择三角形的一个顶点,其它两个顶点都与该顶点做减法操作,即可生成两个向量,通过这两个向量的叉乘结果就可以得到我们的法向量了。求取的表面法线需要被标准化:
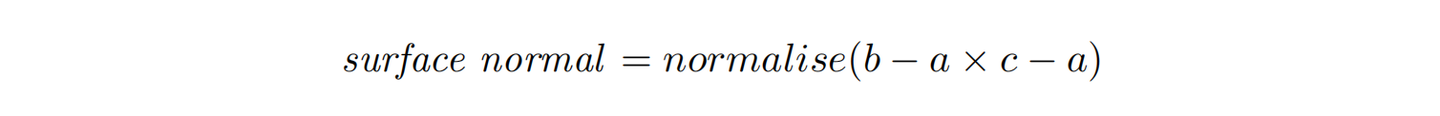
要确定法线所指向的方向,需要知道三角形的环绕方式与所使用的参考系(左手还是右手系),且向量a和b的叉积与向量b和a的叉积方向相反。
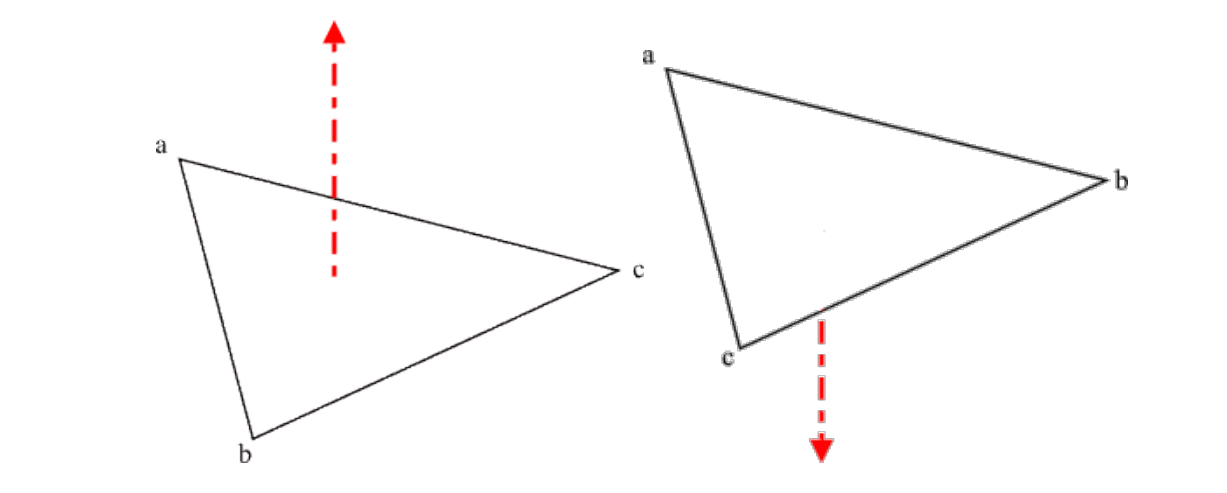
Normal issues
现在已经知道如何计算面法线了,也知道了顶点法线与面法线的区别。从顶点数据来讲,一般顶点数据会附带顶点法线,但是顶点法线是不是等于面法线呢?在有对应索引缓冲区的顶点数据来讲,面与面之间共用了相同顶点,如果每个顶点存储一个法线,而每个面的方向完全不同,会发生什么情况呢? 以下面立方体的顶点a为例:

顶点a是立方体三个面的共用顶点,一个面朝上,一个面朝左,还有一个面朝外。绿色箭头表示对应面的面法线(朝外的法线没有画出),但是哪个面法线对应于顶点a的顶点法线呢? 如果顶点法线可以当作面法线,那么无论选择哪个面作为顶点a的顶点法线,貌似都会引起其它面的面法线指向错误的方向。常见的解决方案是使用共用顶点的各个面的面法线求其标准化向量的和。当法线被顶点着色器之后的阶段插值时,我们将得到一个近似代表每个表面的法线向量:
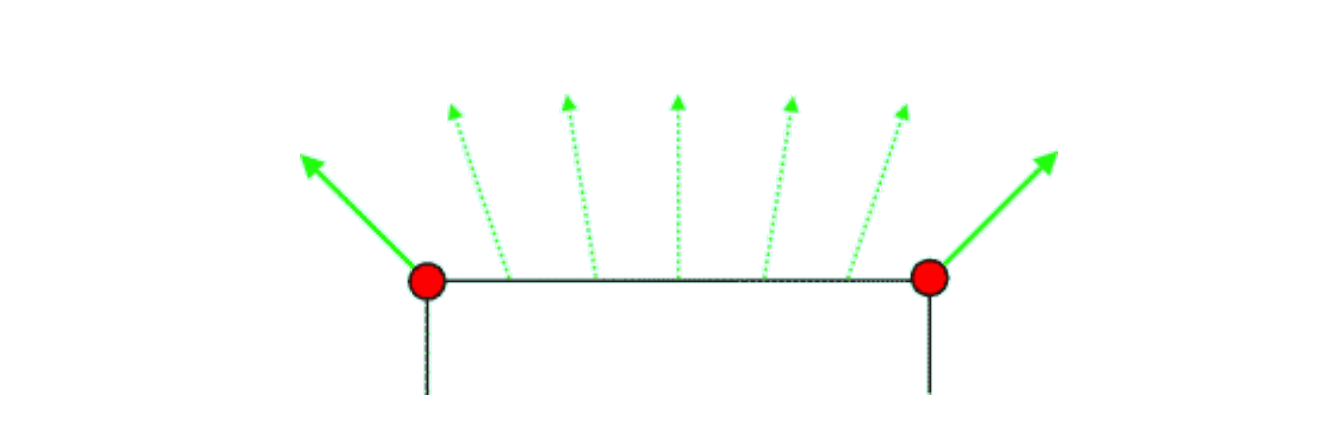
实线箭头是共用顶点的各个面的法线标准化向量求和的结果,虚线箭头是插值的结果
对于顶点法线来说,上述共用顶点的立方体例子确实特殊,所以建模人员通常会放弃对立方体创建索引数据,使得顶点法线可以更精确的应用于各个面。如果非要使用顶点索引数据,上面提供的解决方案也能够很好的工作。
Normal Matrix
顶点通过模型矩阵可以从本地空间转换为世界空间,同样顶点法线或面法线也能够被矩阵转换,但是顶点法线具体要通过哪种类型的矩阵转换呢?实际上与顶点的转换一样,法线也可以通过模型矩阵或模型视图矩阵转换到对应的空间当中,以模型矩阵为例,因为模型矩阵可能包含了位移信息,如果平移变换的越远,那么所得到的法线就会越不垂直于表面,这不是我们想要的。
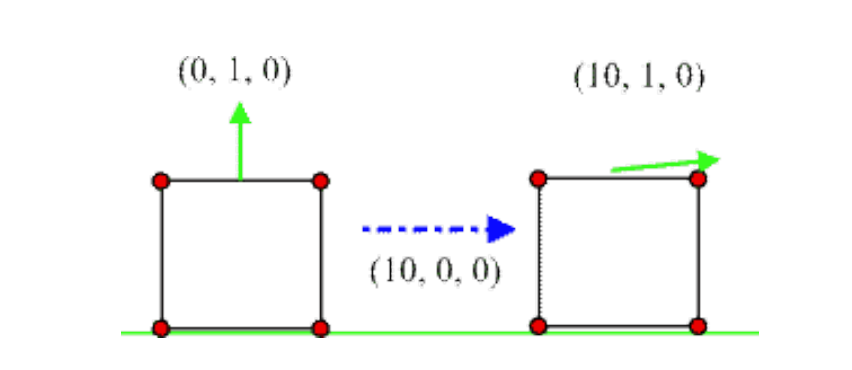
上图的变换结果是把面法线乘上了带位移的模型矩阵,答案很明显,是不可行的。但是如果我们忽略模型矩阵的平移分量(除了去除模型矩阵的平移分量外,还可以使法线向量的w分量设置为0去乘以该模型矩阵, 它会自动忽略矩阵的平移部分的分量),而使用左上方的3x3矩阵部分呢?好吧,这可能行得通,除了在模型矩阵中应用非均匀缩放的情况。
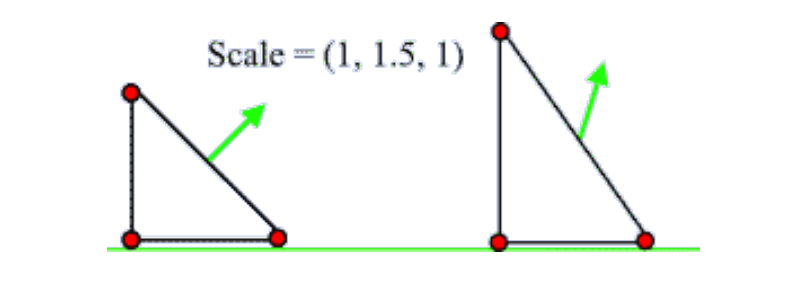
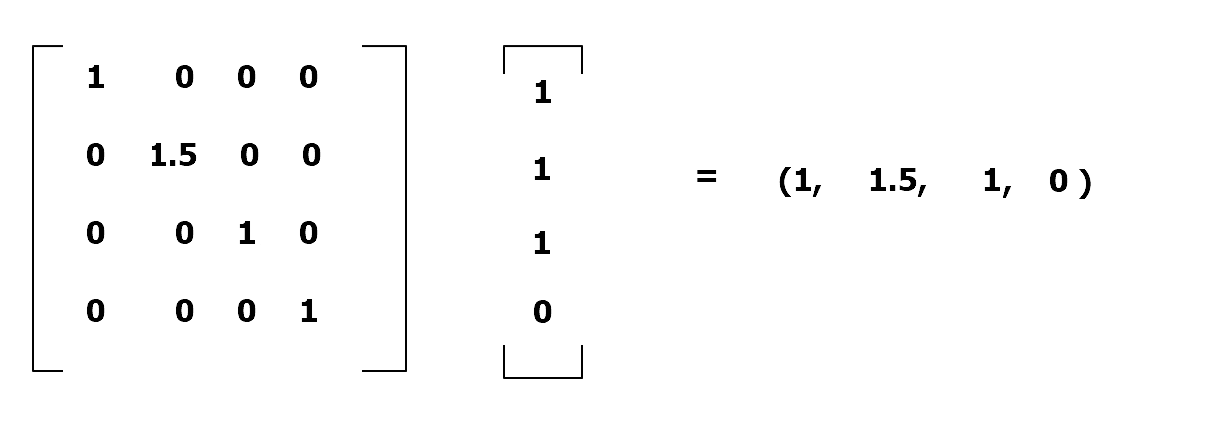
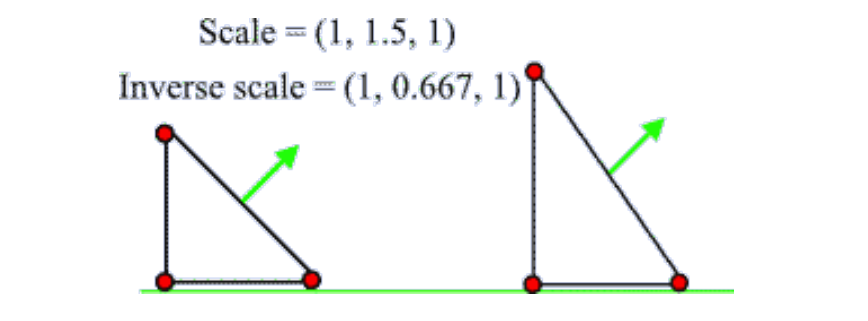
假设当前法线向量为(1, 1, 1),矩阵中的缩放值为(1, 1.5, 1),得到的结果为(1, 1.5, 1):
而均匀缩放值如(3, 3, 3)指向的方向与(1, 1, 1)指向的方向是一致的,且它们的标准化向量也是一致的,所以矩阵是不是均匀缩放值是很重要的。
在模型矩阵(指忽略位移后的模型矩阵)中需要考虑不均匀的缩放终究有点麻烦,因此需要寻找其它的解决方案。为了解决不均匀缩放的问题,我们需要使用模型矩阵的逆矩阵的转置矩阵。这将保留模型矩阵中的旋转,但会反转缩放值,使得法线仍然朝向正确的方向。
如何证明呢?需要引入切线向量。
Tangent
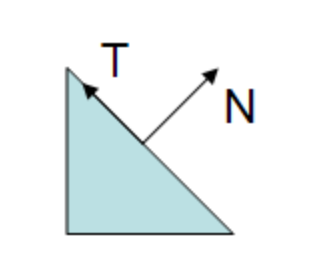
还是以三角形为例,三角形的切线向量是两个顶点间相减得到的,如下面的公式所示,P1与P2代表三角形的两个顶点:

我们可以将法线与ModelView矩阵相乘(也可以与模型矩阵相乘,这不重要):
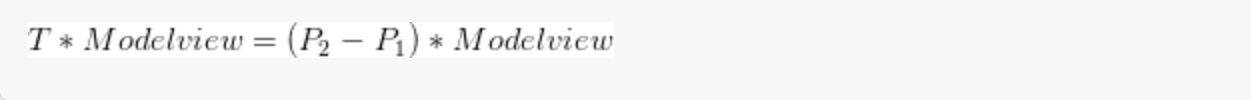
展开后结果为:
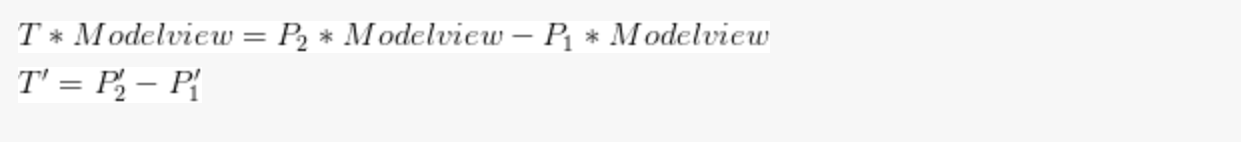
P1'与P2'是变换后的P1点与P2点,
由于P1'和P2'是通过模型视图矩阵变换后的三角形的顶点,所以切线向量T'依旧与三角形的边重合。因此,Modelview/Model矩阵的变换保留了切线,但不保留法线。
Verify
了解了切线向量的概念后,我们就可以做进一步求证。因为切线与法线是互相垂直的两向量,所以N·T = 0(不管变换前还是变换后)。
还是以ModelView矩阵为例,因为ModelView的变换保留了切线,所以切线的变换与矩阵是不是等比缩放并没有关系,所以我们可以放心的取ModelView左上角的3x3矩阵,取名为M,并且假设矩阵G是能够正确变换法线向量到对应空间的矩阵,矩阵值未知,所以求取矩阵G是我们要做的任务:

又因为点积的结果是两向量对应各分量相乘的和的结果( 可转为行向量(GLSL默认使用列向量),用行向量乘以列向量,相当于1x4矩阵与4x1矩阵相乘,结果为1x1是个标量),所以可转换为:

又因为:
所以继续展开:

又因为:
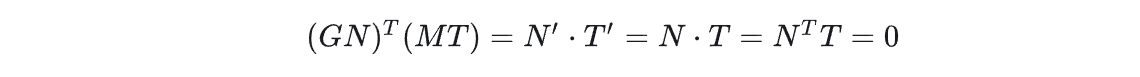
所以:
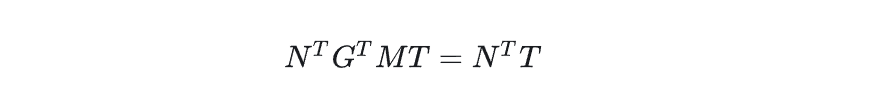
所以:
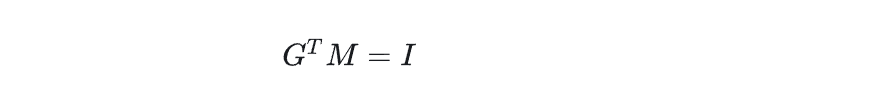
得到G:

推导过程参考可查阅这里,因此变换法向量的矩阵是矩阵M的逆矩阵的转置。其中M矩阵不限定为模型矩阵/模型视图矩阵,一般光照算法是在模型视图空间中进行,所以就需要转换矩阵为模型视图矩阵。另外上面说到M与G取4x4矩阵中左上方3x3部分的值作为矩阵的值,这里是为了便于理解,实际开发还是可以取4x4矩阵,但是需要把切线向量与法线向量的第4分量填充为0,再与4x4矩阵相乘,此时就会忽略矩阵的位移部分。
由于矩阵求逆成本很高,如果保证模型矩阵具有统一的缩放值,仅使用模型矩阵就可以了。