这是Games101的笔记。
线性变换的逆等于该矩阵的转置:

三维变换:

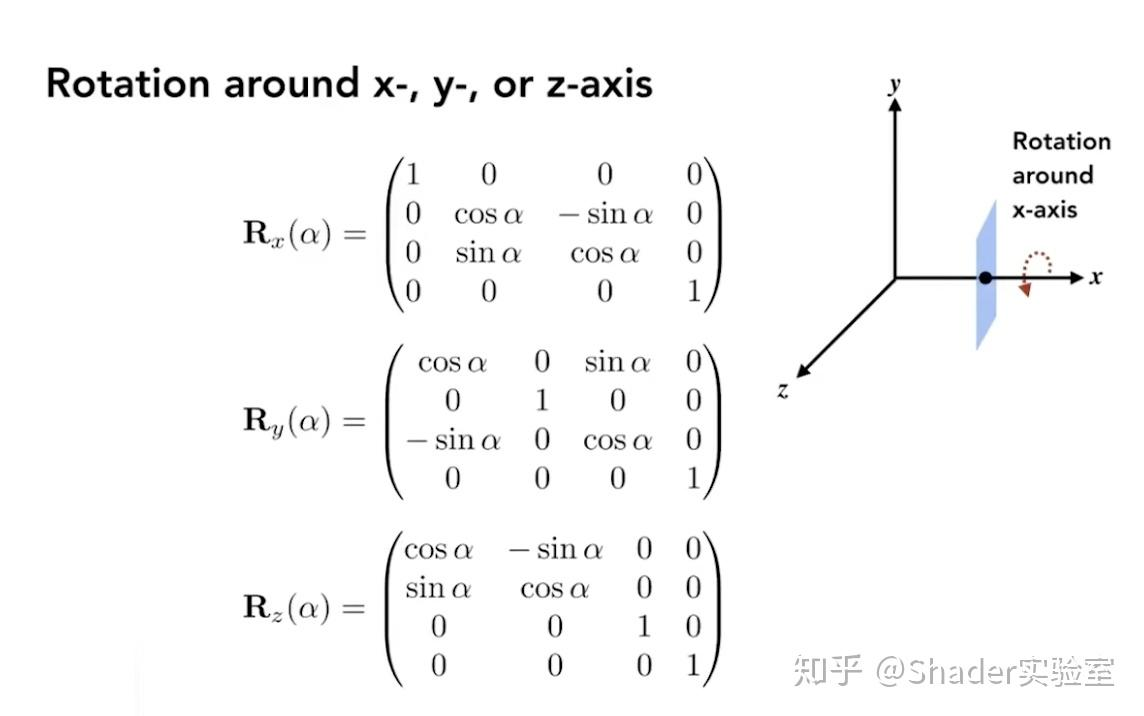

Roll(x),Pitch(y),Yaw(z)
选择Roll-Pitch-Yaw(横滚-俯仰-偏航)作为旋转顺序的原因主要是基于其直观性和在特定应用中的实用性,尤其是在航空和航海领域。这种顺序的选取并不是因为它是“唯一正确”的方式,而是因为它提供了一种符合人类直觉且易于理解和操作的方法来描述物体的姿态变化
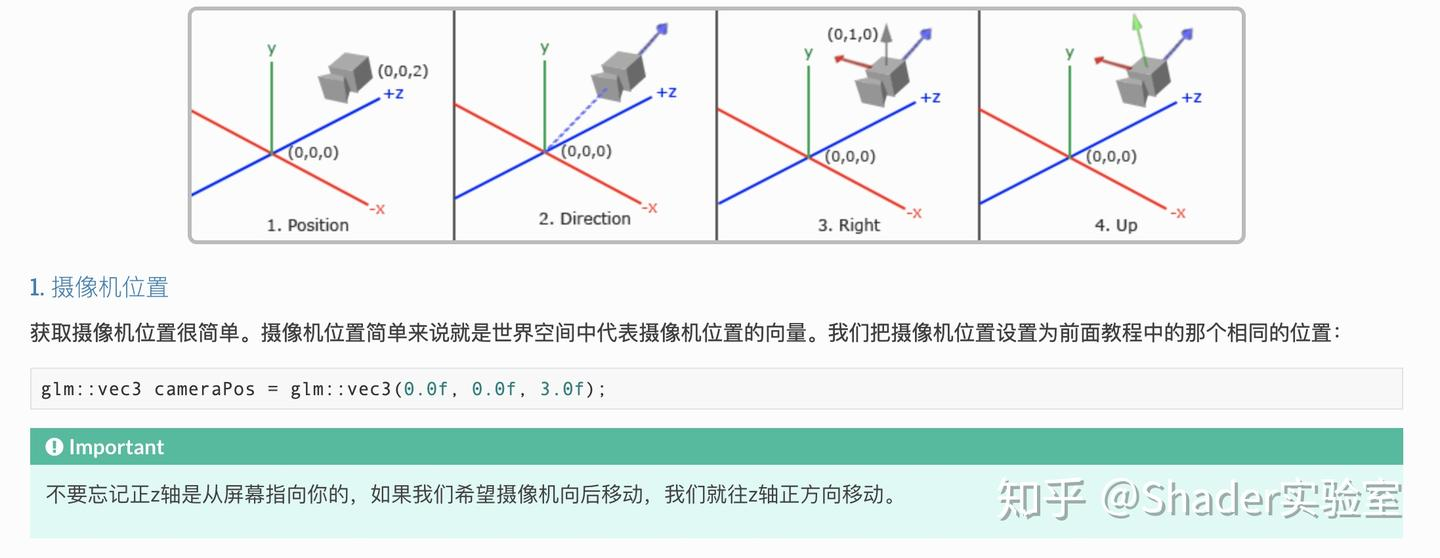
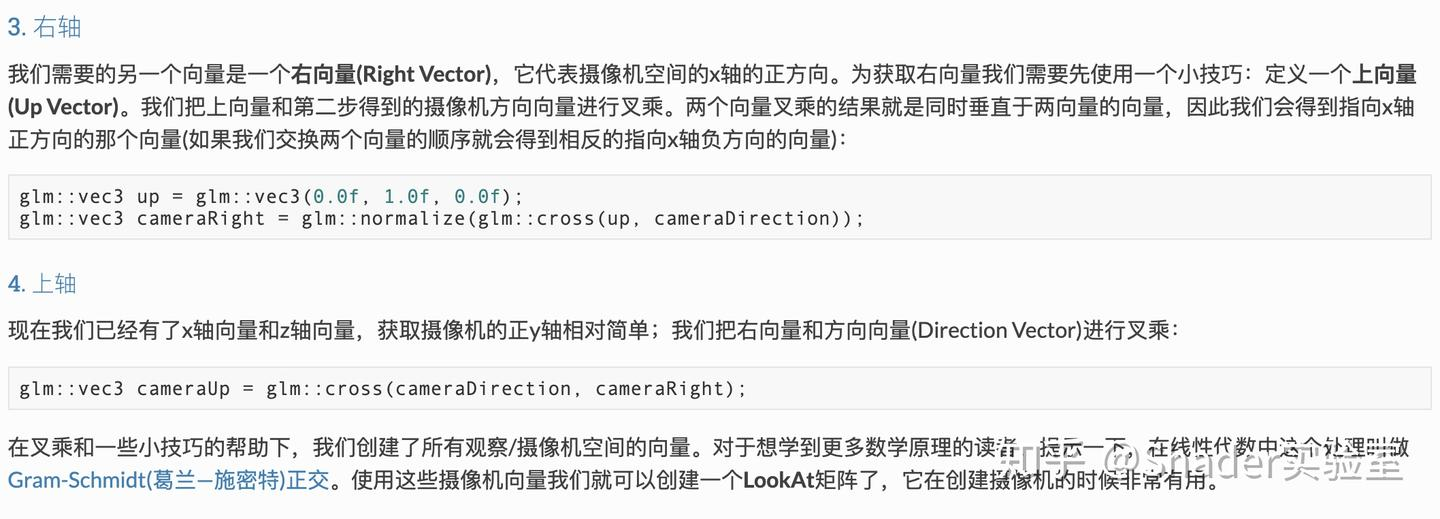
视图变换:

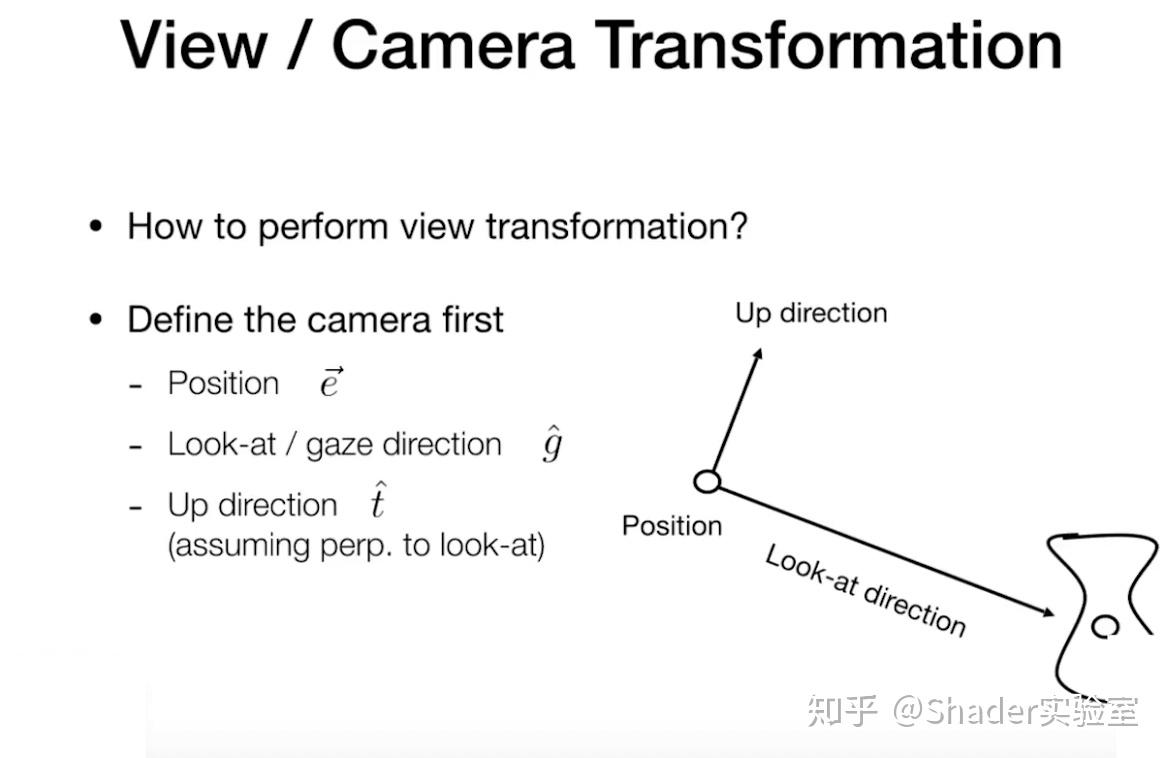
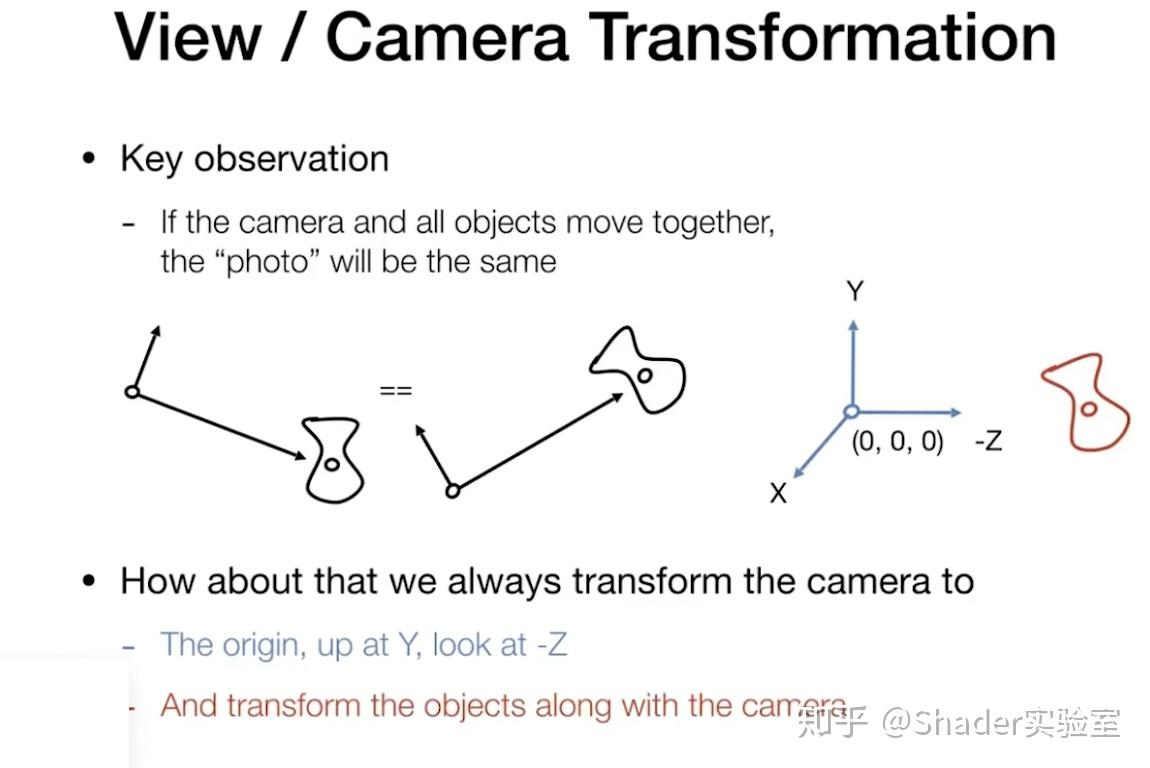
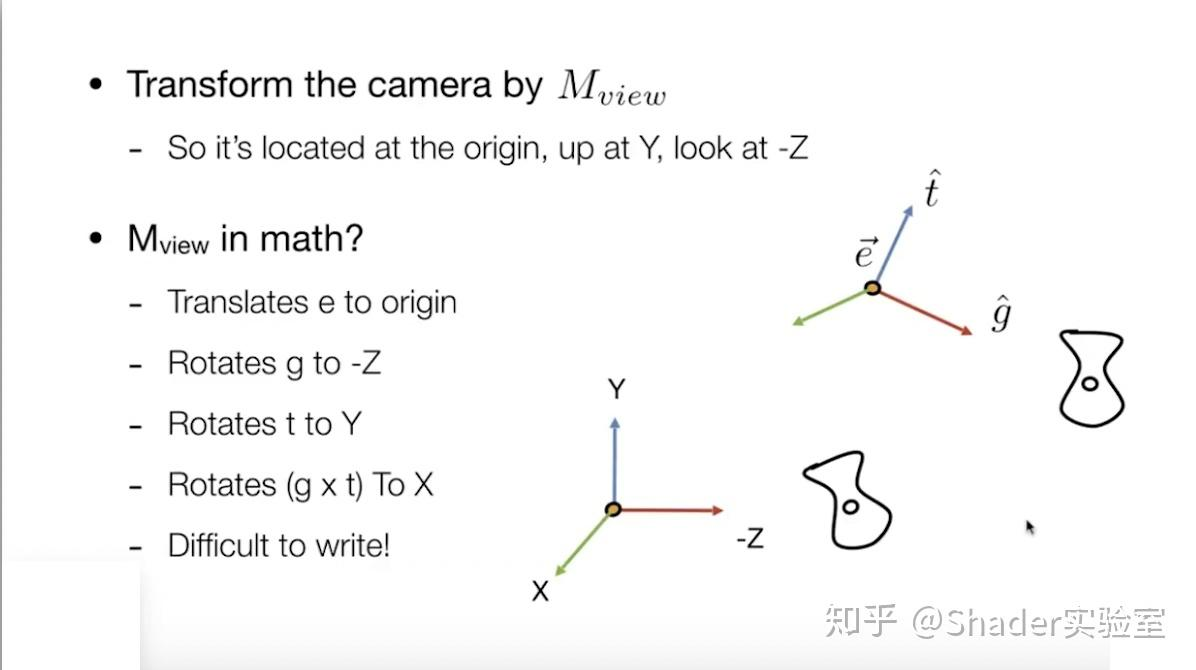


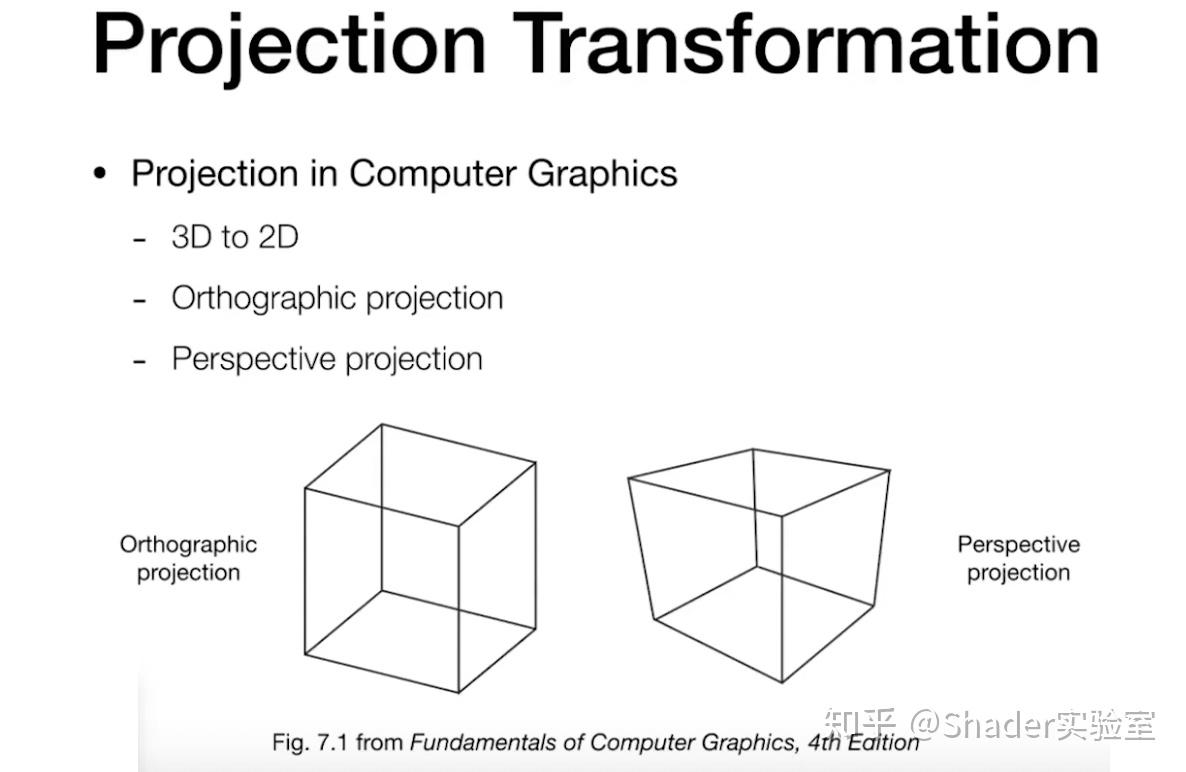
投影变换:
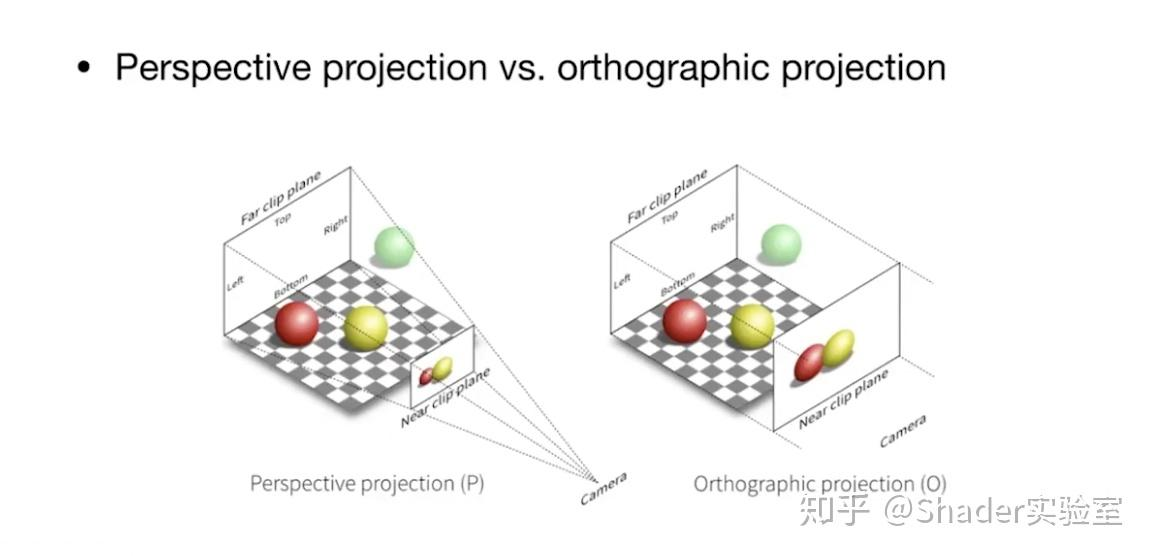
正交投影:
非标准化操作:
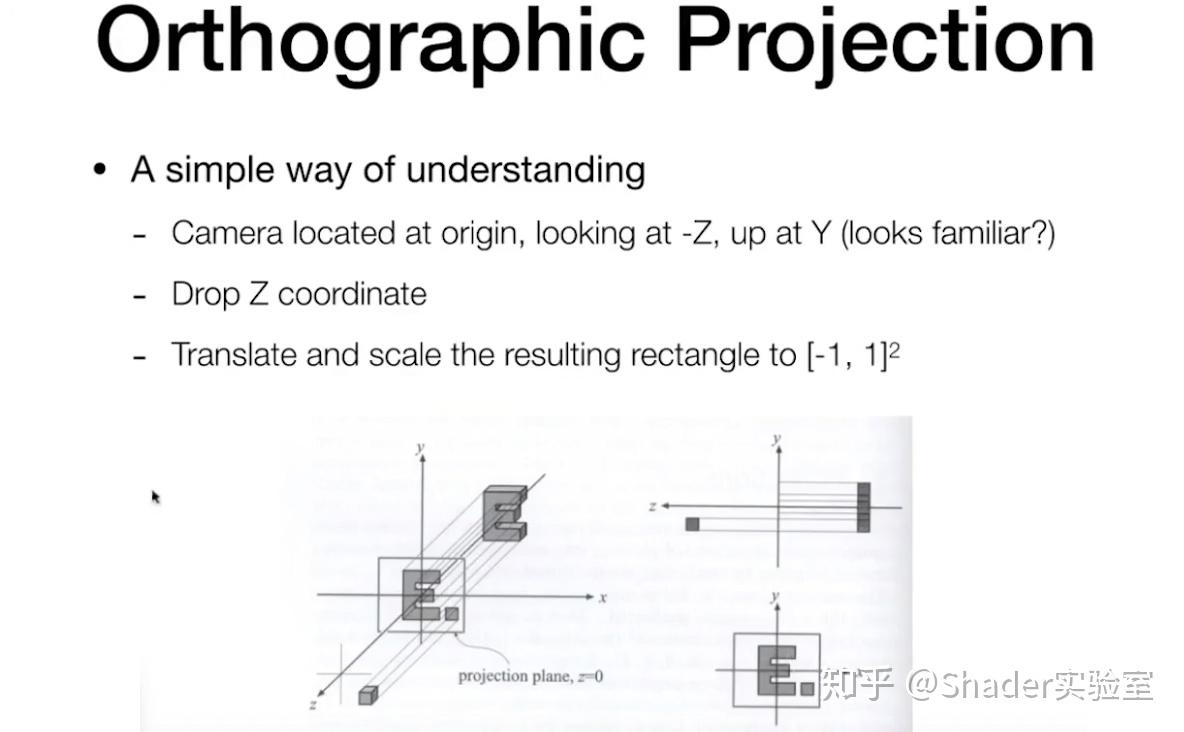
标准化操作:
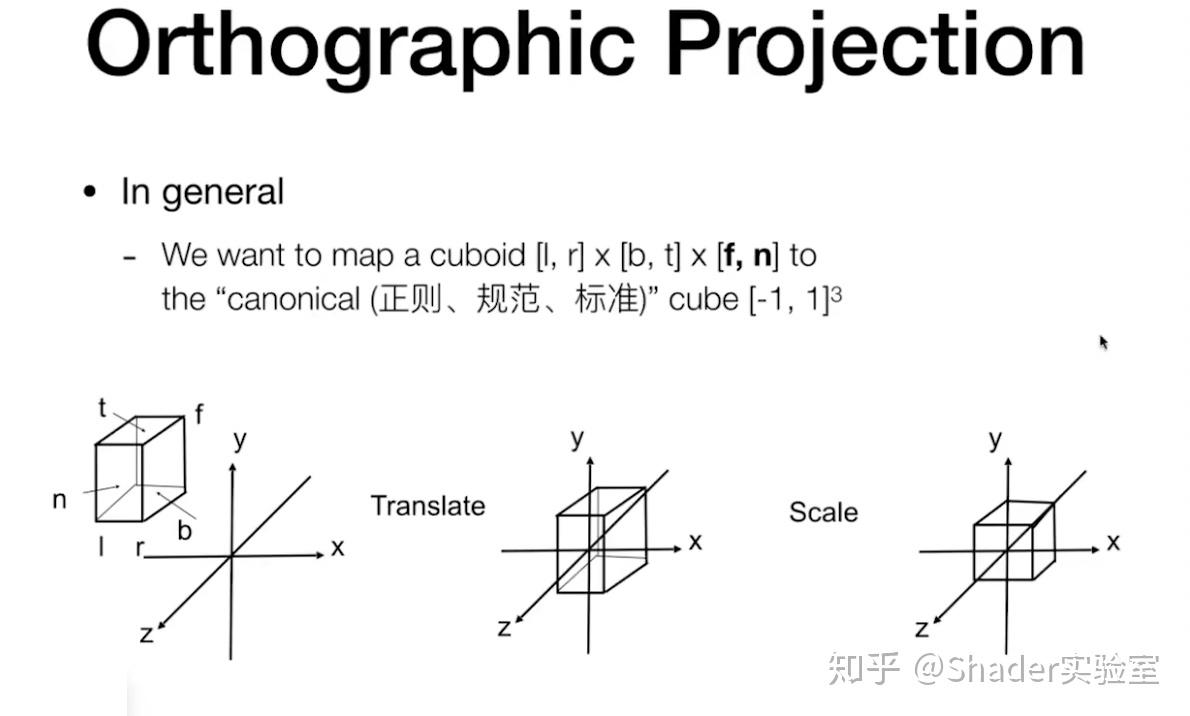
与非标准化的不同:
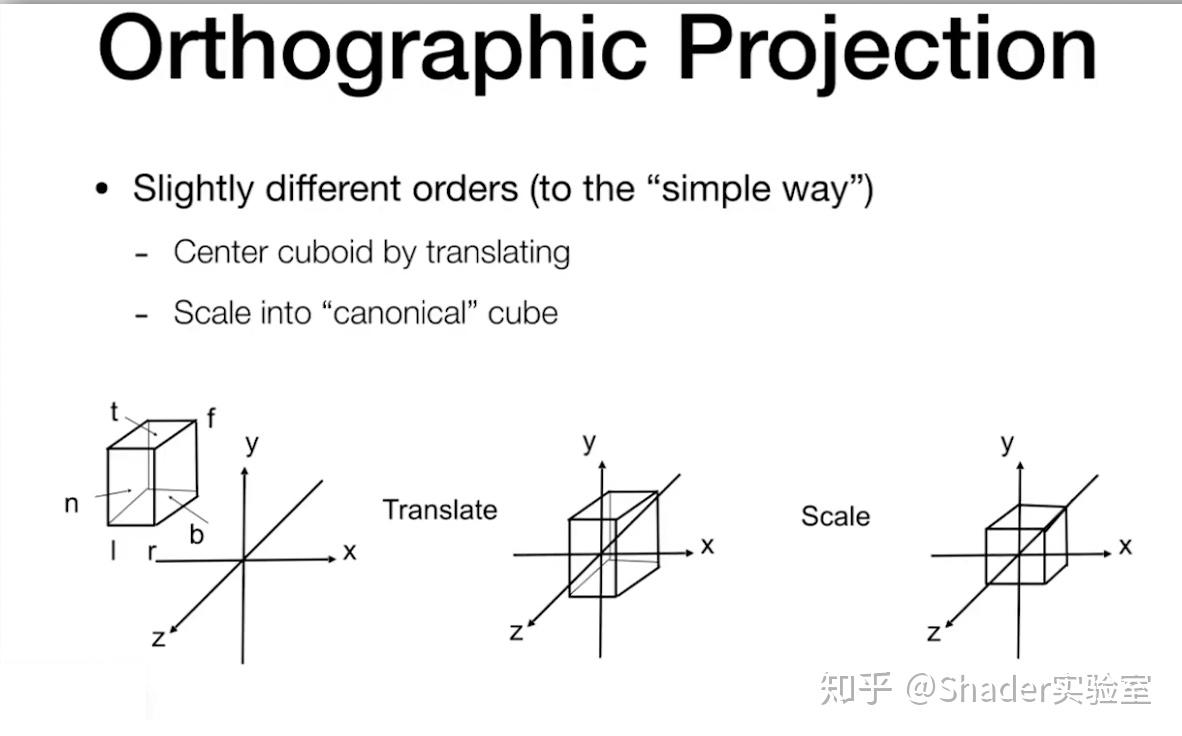
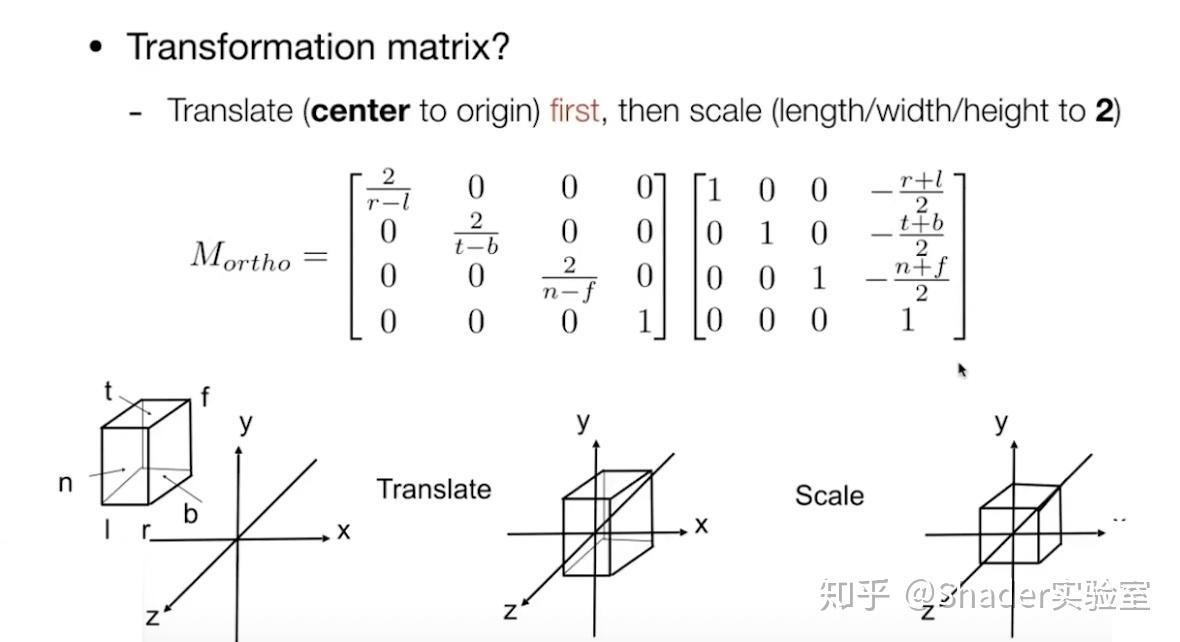
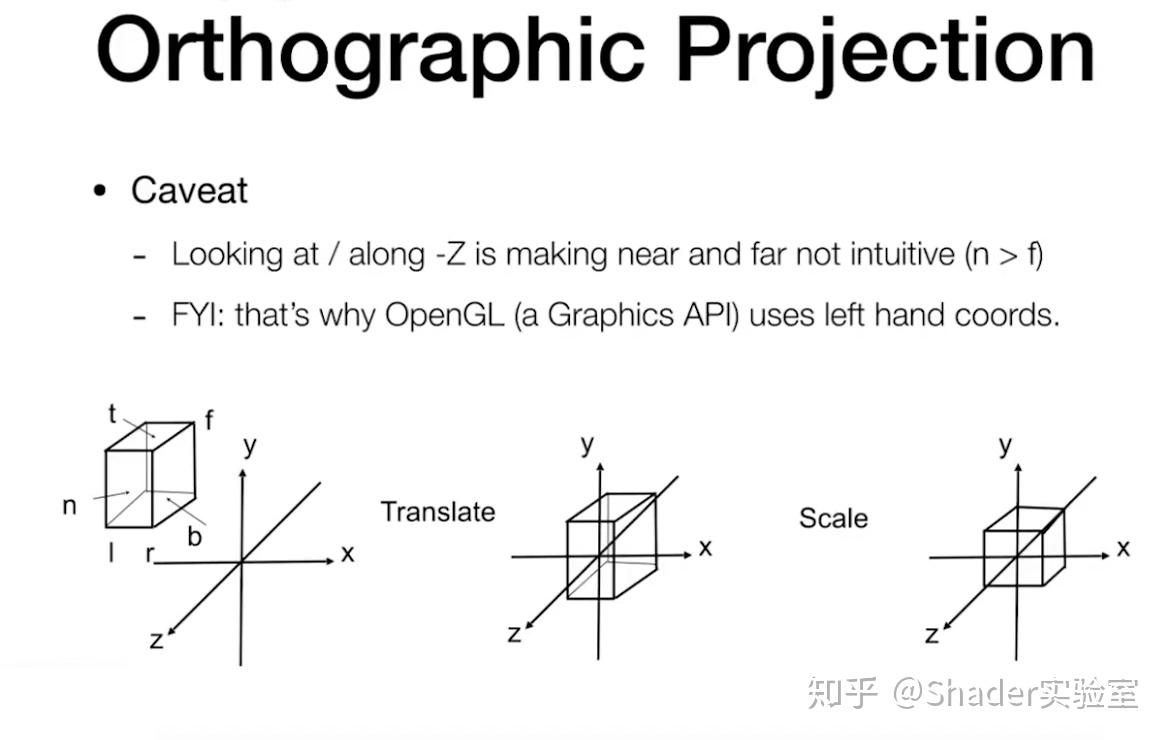
做完变换后,内部的物体是会被拉伸的,但是后面会通过视口变换矩阵重新还原被拉伸的物体。
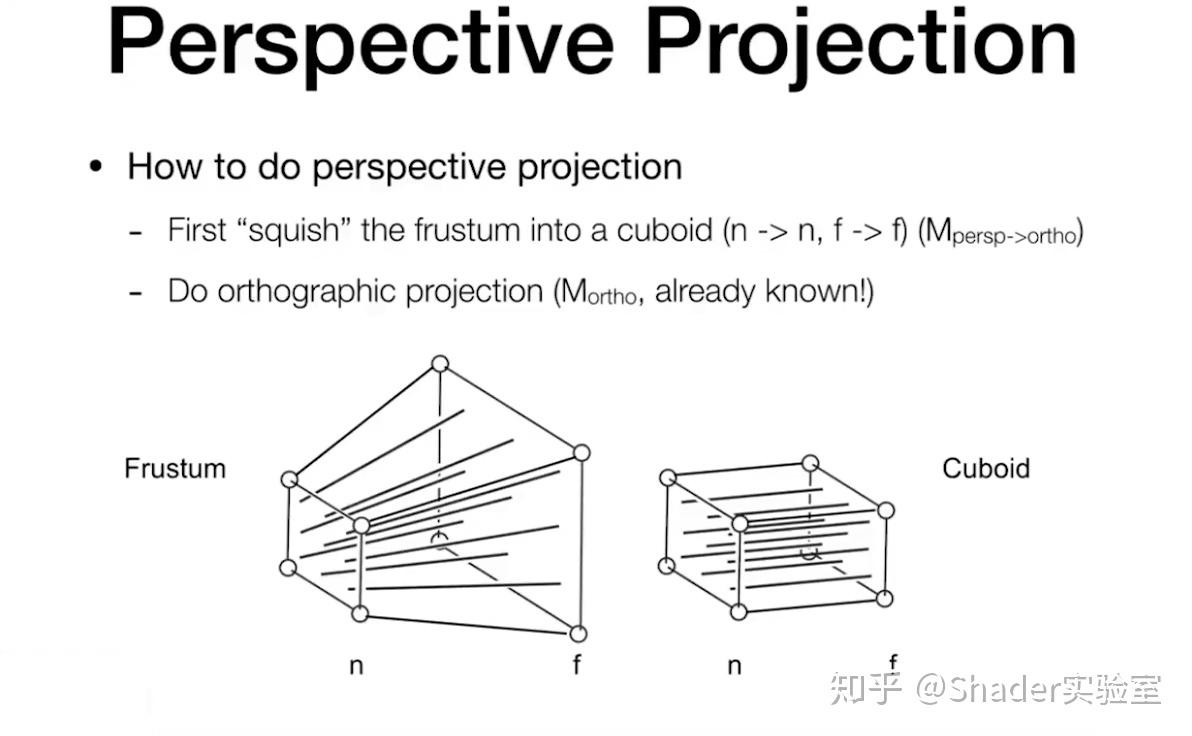
透视投影:
我们已知了正交投影的计算方法,要得到透视投影,可以把透视投影与正交投影做对比,发现透视投影的近平面可以等效为正交投影的近平面,透视投影的远平面是放大后的正交投影的远平面。直观上,我们可以把透视投影的远平面挤压为正交投影的远平面。
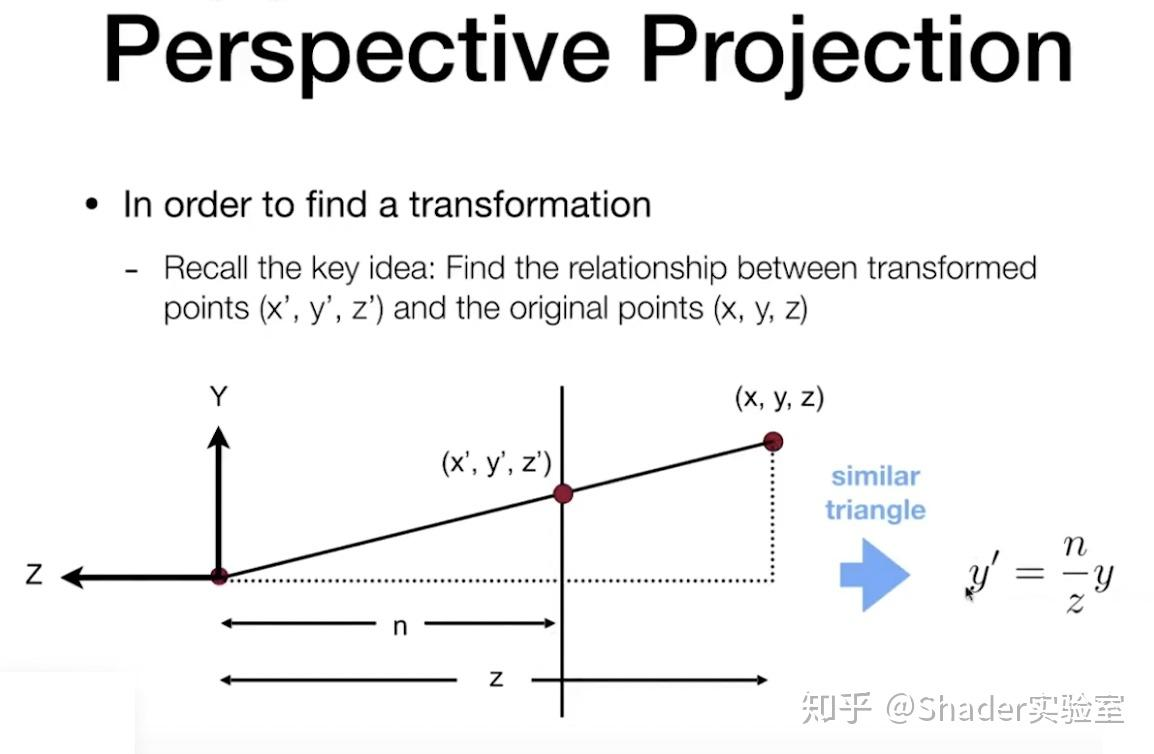
根据相似三角形,(x,y,z)如何映射为(x',y',z')是求取的重点,由于n/z=y'/y,所以 y' = n/z * y :
同样x'也同样满足 x' = n/z * x,但是挤压后的z的值是未知的:
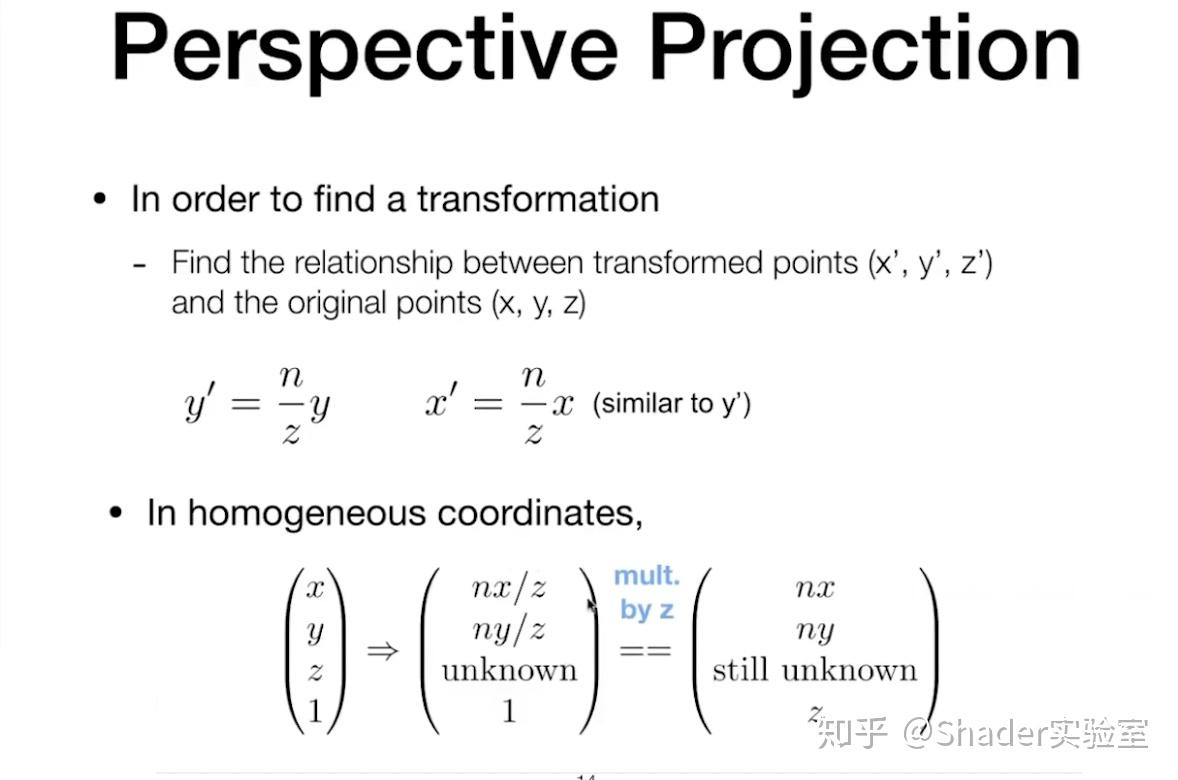
剩下的是求取挤压后的z值,可通过右乘于一个矩阵:

剩下的是求取第三行矩阵的值,观察挤压的过程可以知道近平面与远平面的z值无论如何挤压都是不变的,可根据这个特性求取,先求取n平面上的z值,剩下矩阵第三行的末尾两个数未知:

再取一个特殊点,就是远平面的中心点,这个点不管如何挤压z值都保持不变:

