原理
下图展示了一个角色网格。图中突出的骨骼链称为骨架。骨架为驱动角色动画系统提供了一个自然的底层结构。骨架被外部皮肤包围,皮肤由顶点与多边形构成。与现实中的骨骼一样,骨架中的每一根骨骼都会影响皮肤的形状和位置。数学上,骨骼是由变换矩阵来描述的,通过调整变换矩阵也会相应的改变皮肤的几何形状。因此,当我们对骨骼编辑动画时,附加的皮肤也会相应地实现动画,以反映骨骼的当前姿势。

骨骼与变换
与模型变换空间(Model Space)一样,骨骼变换也有自己对应的变换空间,称为骨骼变换空间(Bone Space)。同样,与模型变换一样,骨骼变换也有局部变换(Local Transform)与组合变换(Combined Transform)的概念。如下图所示。(实际上骨骼变换就是一系列的矩阵变换)
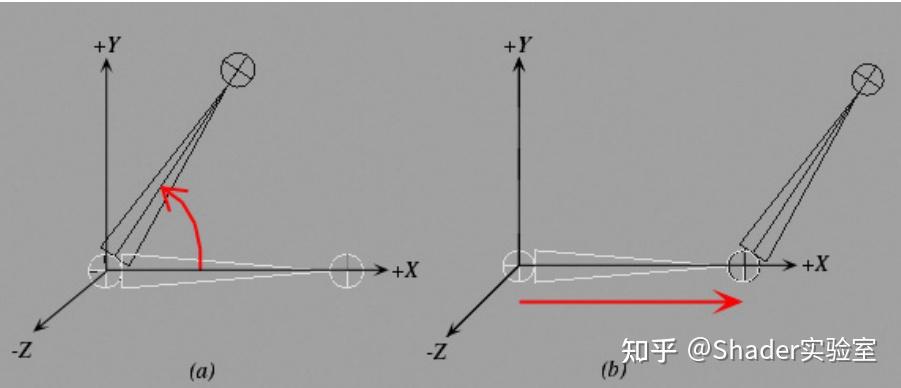
与局部变换不同,组合变换负责实际摆出相对于角色的骨骼,以便构建角色的骨架,如图所示。也就是说,组合变换将骨骼从骨骼空间(Bone Sapce)变换到角色空间。因此,组合变换是用于在角色空间中实际定位和塑造皮肤的变换。
所以要确定角色的姿势,首先应该先计算Bone Space中的组合变换结果,计算过程并不是直接可求取的,因为骨骼之间不是相互独立的,而是影响彼此的位置。暂时不考虑旋转,考虑一下理想的手臂骨骼布局。如图所示:
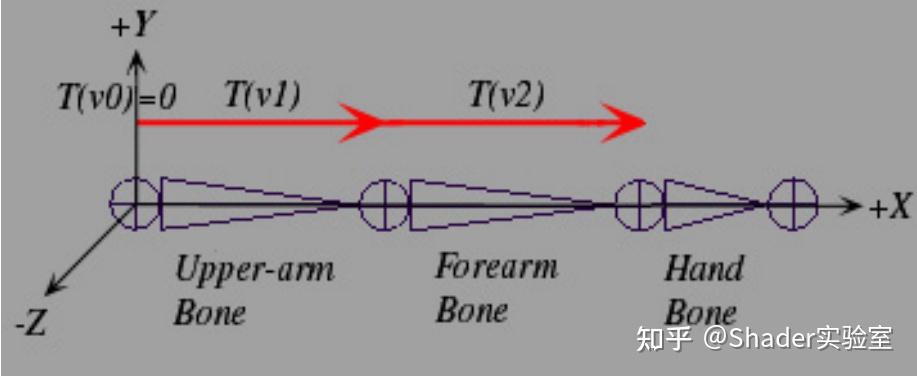
上图HandBone的位置需要通过计算T(v0) + T(v1) + T(v2)决定,也就是说Hand Bone的位置取决于Upper-arm Bone与Forearm Bone的位置所产生的组合变换结果,因为Forearm Bone是Hand Bone的父骨骼,而Upper-arm Bone是Forearm Bone的父骨骼。
刚刚只考虑了位移变换,现在加入旋转变换。如图所示:
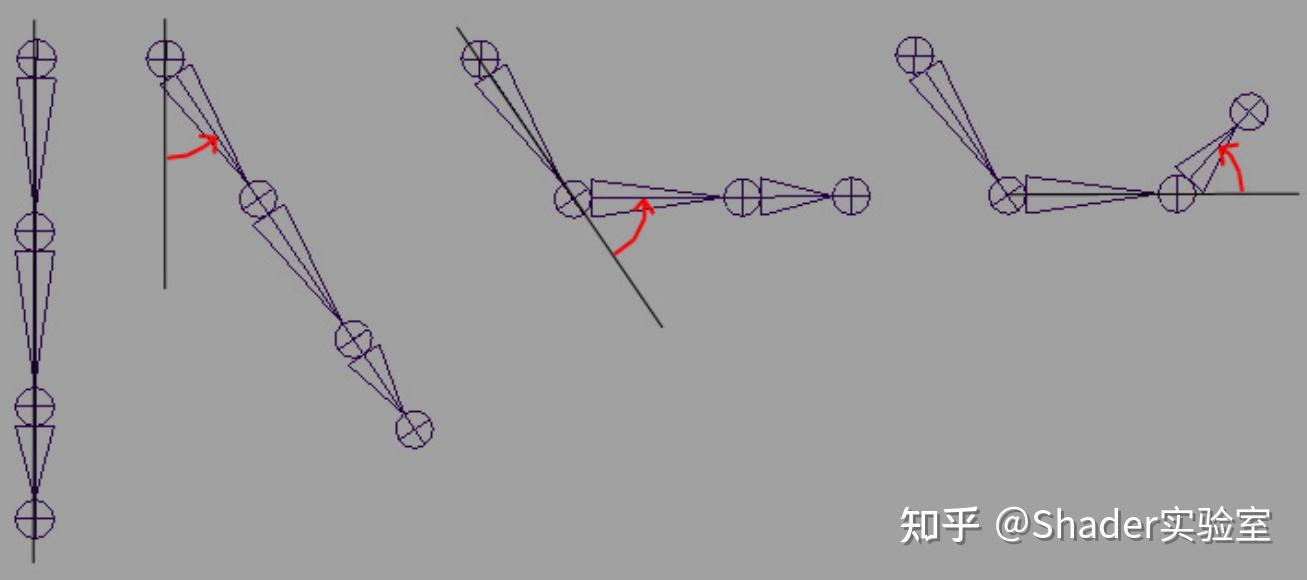
从物理上讲,转动上臂骨骼时,下臂骨骼与手部骨骼也会随之转动。同样的,如果我们旋转前臂,那么手部骨骼也会跟着转动,但是上臂骨骼是不会有变化的。当然,如果我们只转动手部骨骼,那么上臂骨骼与下臂骨骼是不会转动的。由于网格顶点是骨骼变换后的结果,所以要确定角色的姿势,那么首先应该确定各个骨骼局部变换后的结果,然后通过组合变换应用其所有父节点的局部旋转变换来确定,如:要确定手部骨骼的组合变换结果:
$$
Mat(手部) = Mat(手部局部变换) * Mat(前臂局部变换) * Mat(上臂局部变换)
$$
帧与动画
我们主要讨论的是在模型中预定义好的骨骼动画,如在3dmax或maya等建模软件中已经对模型绑定好的角色动画。前面说到,角色的动作是通过骨骼变换矩阵的组合变换来模拟的,那么如何让骨骼动起来是我们下面要讨论的。
假设3D建模人员创建了一个持续5秒钟的机器人手臂动画序列,在0秒的位置手臂的旋转角度为0°,在2.5秒处手臂的旋转角度为60°,在5秒处手臂相对0秒位置时旋转角度为30°。
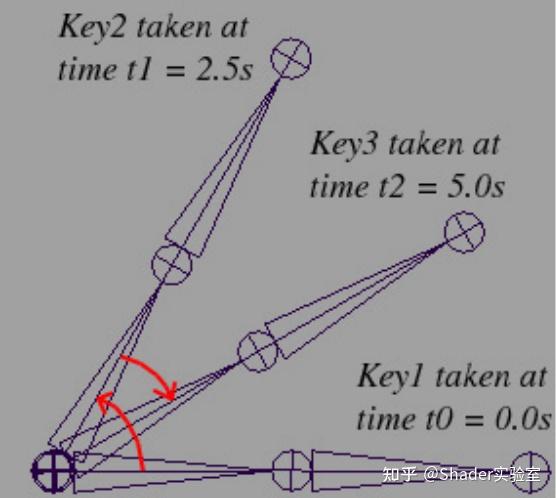
0s => 0°,2.5s => 60°,5s => -30°。我们把在特定时间点上的特定变换状态称为关键帧,那么骨骼的关键帧就是在特定时间点上的特定变换状态所形成的特定姿势就可以称为骨骼关键帧。在一个动画序列中,骨架中某些特定的骨骼(Bone)通常都会设定几个关键帧。关键帧的变换状态常用旋转四元数、缩放向量和平移向量表示。
回到刚刚的例子,我们在五秒内只设定了3个关键帧,但是我们知道要使一个动画平滑或者动画不至于出现"跳跃"的现象,五秒内仅仅设定三个关键帧是明显不够的,那么再多设定几个关键帧?也能解决问题,但是这种方式很繁杂,增加了多余的工作量,而且尽管多设定了一些关键帧也不一定能够完全保证平滑。那么有没有办法通过头尾两个关键帧让计算机自动计算两个关键帧内的变换状态呢?如图所示:
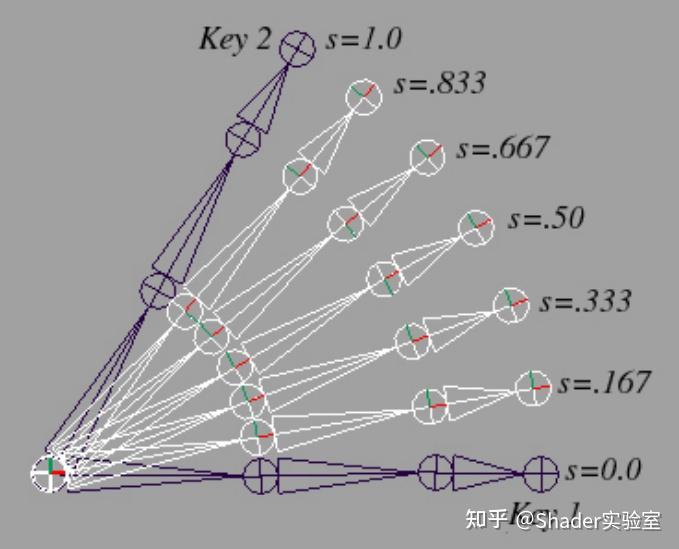
这是接下来要讨论的骨骼关键帧插值。
骨骼关键帧插值
如上图所示,从Key1到Key2的中间姿态是通过关键帧插值来计算的。也就是说,给定关键帧Key1和Key2,我们可以通过数学插值从Key1描述的骨骼姿态到Key2描述的骨骼姿态来计算中间姿态。当插值参数s从0移动到1时,中间姿态分别从Key1移动到了Key2。因此,s表示从一个关键帧到另一个关键帧的混合因子。
最常用的插值方式是**线性插值**(其它插值有Hermite样条插值等),但是骨骼的线性插值只适用于位移变换与缩放变换,不适用于旋转变换,因为在三维空间中旋转要更复杂,它必须使用四元数来表示旋转并用球面插值来正确地计算基于四元数的旋转。
注意:由于矩阵在处理旋转过程中无法有效的进行插值处理,所以一般不对矩阵直接进行插值处理。因此关键帧的变换数据通常以旋转四元数、缩放向量和平移向量(RST)存储,而不是以矩阵的形式存储。在对所有骨骼(Bone)的RST值进行插值(即旋转四元数、缩放向量和平移向量插值)之后,我们可以继续利用插值后的RST值为每个骨骼重新构建骨骼矩阵。
但是由于骨骼的特殊性,通常不会对平移与缩放进行插值,更多的是对骨骼的旋转变换进行四元数插值。
上述只对一根骨骼的插值变换进行了描述,为了使整个骨架动画化,就必须对骨架中的多根骨骼进行插值。我们把所有这些骨骼动画内插的过程称为interpolated-skeleton。
骨骼与蒙皮
我们已经知道了角色动画需要骨骼作为驱动,也知道了通过关键帧定义骨骼变换后,需要做对应的插值,才可使骨骼动画变得更加平滑。但是我们还不知道骨骼与蒙皮的关系,需要明确的是蒙皮的概念:简单的讲,蒙皮即是角色的网格。骨骼与蒙皮的关系即是骨骼与角色网格(模型顶点)的关系。用一个简单的例子来描述他们间的关系:假设建模人员建立了一个手臂骨骼,并在Bone Space中建立手臂模型的网格顶点,这个过程可近似看成骨骼绑定的过程("近似"是因为确实有个绑定空间,这里只是为了便于理解),这里不需要纠结是先有骨骼还是先有网格,而要说明的是,要想让骨骼的运动影响蒙皮,那就需要把蒙皮与骨骼放置在同一参考坐标系中,而影响的过程就是把网格顶点与对应骨骼的Bone Sapce坐标系对应,使得骨骼的变换能直接影响对应的蒙皮(即网格顶点)。这种技术也叫做Rigid Body Animation。
到这里我们已经了解了不少骨骼动画的相关知识了,但是按照目前的知识去解析一段上臂与下臂屈伸的模型动画,会发现骨骼连接处的蒙皮会出现非常生硬的穿帮现象,如图所示:

顶点混合(Vertex Blending)
刚刚说到Rigid Body Animation存在一定的缺陷,比如上图中人物的骨骼蒙皮分割成了互不相连的部分。为了解决这个问题,我们需要把角色的皮肤当作一个连续的网格来处理,如图所示:
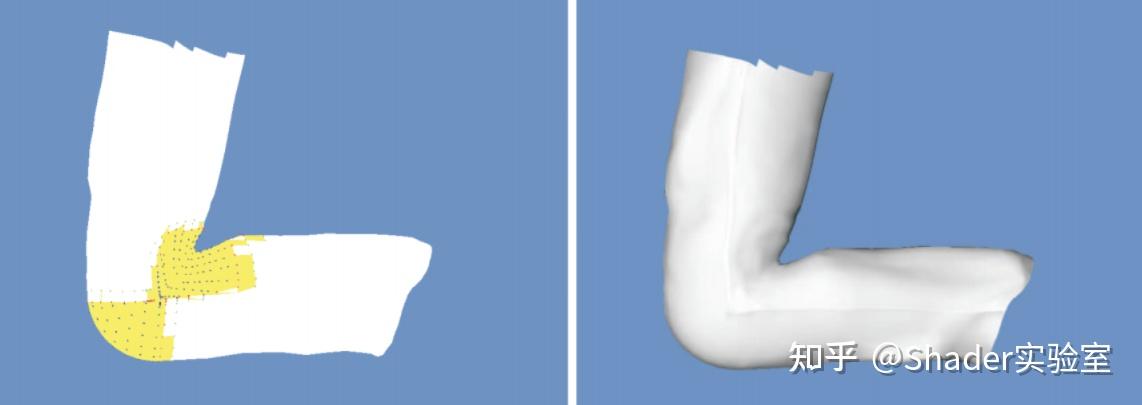
观察上图可以发现,蒙皮网格是连续的,关节附近的顶点似乎同时受到上臂和前臂的影响;换句话说,关节附近顶点的位置是由上臂与前臂两个骨骼同时影响的结果,数学概念称为加权平均值,这一概念是顶点混合(Vertex Blending)算法的核心思想,也就是说,部分皮肤可能受到不止单一骨骼的影响。建模人员常称它们为权重。
在探讨顶点混合具体细节之前,需要处理一个问题:上面提到蒙皮的运动需要在对应骨骼的Bone Sapce中建立对应关系,但是要具体实施顶点混合,就需要将角色的网格建立在角色的模型空间中。因此,由于顶点不在Bone Space中,所以不能简单地使用骨骼的组合变换。
为了解决上述问题,需要引入新的变换矩阵: Offset Transform, 骨架中的每根骨骼都有一个对应的Offset Matrix,Offset Matrix指的是蒙皮网格顶点绑定到骨骼时,从绑定空间到相应的骨骼空间(Bone Space)的变换矩阵。绑定空间指的是角色网格在应用任何骨骼变换之前的默认姿势(坐标空间)(也就是此时Bone Matrix为identify),比如T-Pose。

所以第i根骨骼的最终变换矩阵Fi为:
$$
Fi = MiCi
$$
其中Mi为第i根骨骼对应的Offset Matrix,Ci为第i根骨骼对应的组合变换矩阵(combined matrix)。
上面说到顶点受骨骼的影响,影响程度称为权重。说明了同一个顶点可能会受不同骨骼的影响,那么同一个顶点受越多骨骼的影响,最终必然导致计算量加大,效率降低,所以普遍做法是:同一个顶点最多限制为受4根骨骼的影响。一般会如下定义顶点结构:
struct Vertex
{
vec3 pos;
vec3 normal;
vec2 uv;
vec4 jointIndices;
vec4 jointWeights;
}
其中jointIndices代表四根骨骼的索引(也就是对应骨骼矩阵的索引,之所以不直接存储矩阵,是为了减少内存消耗),jointWeights代表对应骨骼影响顶点的权重。不一定4根骨骼都会对相应顶点产生影响,比如只有两根骨骼产生了影响,那么另外两根骨骼的权重值就为0,且骨骼的索引可能为-1(取决于项目规范)。顶点的最终位置的计算结果如下所示:
$$
V' = W_0VF_0 + W_1VF_1 + ... + W_{n-1}VF_{n-1}
$$
上式中w0 + w1 + ... + wn-1 = 1,即100%