Introduction
在每款3D游戏中,都会有这类应用场景,比如用户需要点击场景中的某些游戏物体。也许是在诸如RTS类型游戏中选择一个建筑单元,或者在RPG类型游戏中打开一扇门,或者在关卡编辑工具中删除一些几何体。这些功能尽管在概念上很简单,但是实现过程还是有些细节容易出错。
比如如何通过给定鼠标在窗口中的点击位置,判断在游戏场景中选择了哪个游戏物体?
一种方法是通过鼠标在屏幕中点击的位置生成一条射线,然后将其与世界空间中的几何物体进行相交测试,找到与该射线初次碰撞的物体。或者,我们也可以通过采样深度缓冲区(比如在延迟渲染中介绍的方法)并执行逆变换来确定用户点击的实际世界空间中的位置。从技术上讲,还有第三种方法,使用游戏对象的ID Buffer借助深度图的方式,但这有许多限制,使得它不适合广泛使用。
本篇介绍了通过使用逆变换如何让鼠标从屏幕上的位置推导出世界空间坐标。
在介绍坐标空间的逆变换前,需要先回顾下渲染管线空间变换相关的数学方法。
The View Transformation
渲染管线会将模型空间中的点,通过一系列的转换矩阵,转换到视口空间中:
添加图片注释,不超过 140 字(可选)
上面的转换矩阵不一定是按固有的矩阵逐步进行的,比如可以把模型矩阵与视图矩阵组合为模型视图矩阵(可用M表示),它可以将模型空间的点p转换为视图空间的点v。模型空间和视图空间可以都使用右手坐标系,+Y向上,+X向右,-Z 指向屏幕:
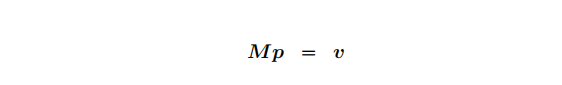
添加图片注释,不超过 140 字(可选)
接下来就是投影矩阵(可用P表示),可以将视图空间上的点转换为裁剪空间。裁剪空间使用的是右手坐标系(+Z向内):
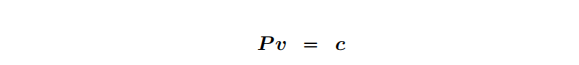
添加图片注释,不超过 140 字(可选)
经过裁剪空间转换后,需要通过透视除法将裁剪空间中的齐次坐标点c转换至标准化设备空间中的点n。标准化设备坐标系是左手坐标系,其中w=1,它的范围为(−1、−1、−1)到(+1、+1、+1):
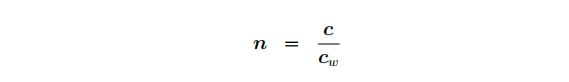
添加图片注释,不超过 140 字(可选)
最后是视口变换矩阵V,它将n转化为最终的视口坐标w。这里有可能包含其中一个轴的反转(视viewport坐标原点是左上角还是左下角决定):+Y向下而不是向上。视口的深度值是通过将NDC的Z坐标从(-1,1)重映射为(0,1)的范围,0在近裁剪平面,1在远裁剪平面:
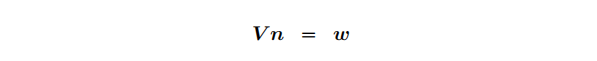
添加图片注释,不超过 140 字(可选)
我们的目标是将鼠标在视口坐标系中的位置转换回世界空间。因为我们不需要渲染模型,所以模型空间和世界空间在说法上是一致的。
The Inverse View Transformation
为了把屏幕坐标转换为世界坐标,我们需要做与上述转换完全相反的过程。
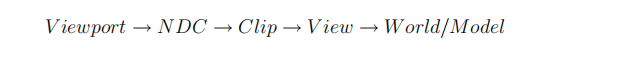
添加图片注释,不超过 140 字(可选)
由于转换过程比较复杂,一旦中间的哪个转换步骤出现问题,那么结果必然出现问题。
Viewport → NDC → Clip
第一步是将视口坐标转换为裁剪空间坐标。通过给定视口宽度w和高度h,视口变换V将一个归一化的设备坐标n转化为了视口坐标。那么我们的视口坐标v的结果就是:
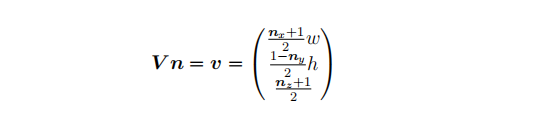
添加图片注释,不超过 140 字(可选)
通过上式就可以求取n:
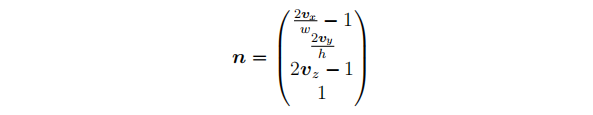
求取过程把v看成[vx, vy, vz]
求取过程还算顺利,但是有一个问题是Vz的值是什么?要求取Vz可以通过采样深度图来求取Vz,或则如果求取的是射线而不是具体的世界空间坐标,可以把z值直接设为1。
接着需要转换为裁剪坐标,由于裁剪坐标转为NDC坐标是除以裁剪坐标的w值,但是因为目前n的w值已经为1了,非0值的w只是同一坐标点的不同表示,所以这一步可以跳过。
Clip → View
通过将视图空间中的向量v乘以投影矩阵P,可以将其转换为剪辑坐标c:
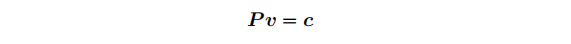
添加图片注释,不超过 140 字(可选)
基于上述公式,要求取v,我们可以将c乘以投影矩阵P的逆矩阵进行,但是由于计算逆矩阵是有时间成本的, 如果我们通过已知条件构建投影矩阵的同时构建逆投影矩阵,就可以避免计算4x4矩阵的逆矩阵了。
以OpenGL为例,透视投影矩阵P的形式为:
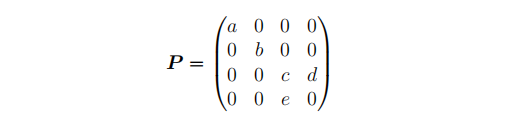
添加图片注释,不超过 140 字(可选)
上述各字母(a, b, c, d, e)表示的具体参数信息取决于透视投影矩阵的具体算法(更多信息建议看一下gluPerspective的手册)。这些辅助系数会将Vx、Vy和Vz缩放并偏移至裁剪空间中,同时将-Vz分配给Cw。
所以要从视图坐标v转换到裁剪坐标c需要经过如下变换:
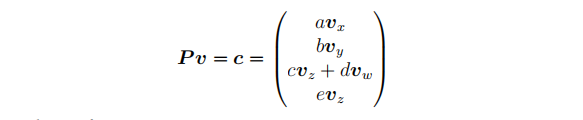
添加图片注释,不超过 140 字(可选)
所以求取v,可以得到:
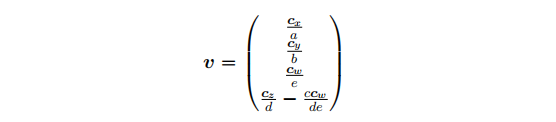
添加图片注释,不超过 140 字(可选)
通过上述的v坐标,封装成逆投影矩阵为:
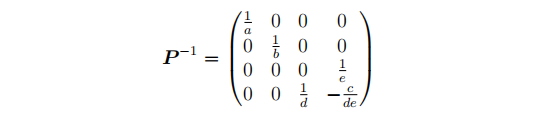
添加图片注释,不超过 140 字(可选)
现在,通过裁剪空间坐标计算视图坐标是很简单的:
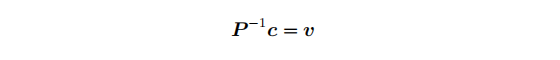
添加图片注释,不超过 140 字(可选)
我们无法保证Vw恒等于1,所以我们要重新调整v的坐标:
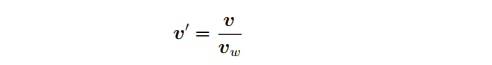
添加图片注释,不超过 140 字(可选)
View → Model
最后,我们只需要求取如何从视图坐标转换到世界坐标,可以通过将视图坐标与模型视图矩阵的逆矩阵相乘求取。同样的,直接求取逆矩阵会有时间上的成本,所以需要避免直接求取逆矩阵。我们可以把模型视图矩阵分解为两个矩阵一个是平移矩阵(以相机位置为原点),然后是旋转矩阵(相机的朝向),该旋转矩阵要求逆可以通过转置完成。所以模型视图矩阵的逆矩阵的求取就可以通过先求取逆向旋转后,再把平移分量取反进行平移。
如果初始模型视图矩阵为M,它由左上角3x3矩阵R和第4列的平移向量t组成:
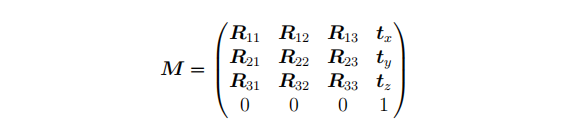
添加图片注释,不超过 140 字(可选)
然后可以通过R矩阵的转置与相机的平移向量t来构建模型视图矩阵的逆矩阵:
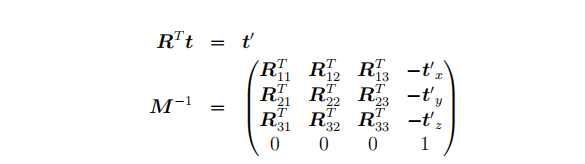
添加图片注释,不超过 140 字(可选)
现在我们有了模型视图矩阵的逆矩阵,现在可以用它来把我们的视图坐标v转换成世界坐标,从而得到坐标点w:
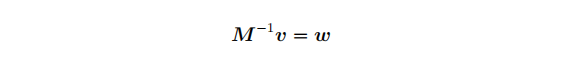
添加图片注释,不超过 140 字(可选)
如果我们在视口坐标中知道了z值,那么鼠标点击的世界空间中的位置也能够直接获取到了,如果并不知道z值,那么它的位置就有很多可能性,我们可以利用它来构建一条以相机位置a为起点的射线:
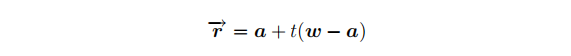
添加图片注释,不超过 140 字(可选)
如果觉得上述求取射线的公式实现稍显复杂,我们可以在与模型视图矩阵的逆矩阵相乘时,把v中的w(这是向量的w分量)直接设置为0即可在求取到世界空间坐标点w(这是坐标点与不是向量的w分量)时忽略平移,求取后的结果即为射线向量,如果需要求取世界空间中的具体点这种做法就不可取了。
现在应该会有两种情形:如果在视图坐标中已知了z值,那么就可以求取到世界空间中对应于鼠标点击位置的实际世界坐标点,如果无法知道z值则可以求取到表示鼠标点击方向的世界空间射线。如果有一个实际的点,我们可以搜索世界空间中的所有几何体,看看它最接近哪一个。如果有了射线,那么我们需要在射线和世界空间中几何体之间执行相交测试,并找到最接近近裁剪平面的几何体。两种方法的实现应该都不复杂。
本文参考:
- Mouse Ray Picking Explained:Brian Hook