Introduction
我们从SceneManagement篇中介绍了Frustum如何进行场景剔除,但是没有详细介绍如何提取Frustum平面,那么给定Model,View与Projection矩阵如何提取Frustum平面呢?我们还是使用Opengl进行阐述。
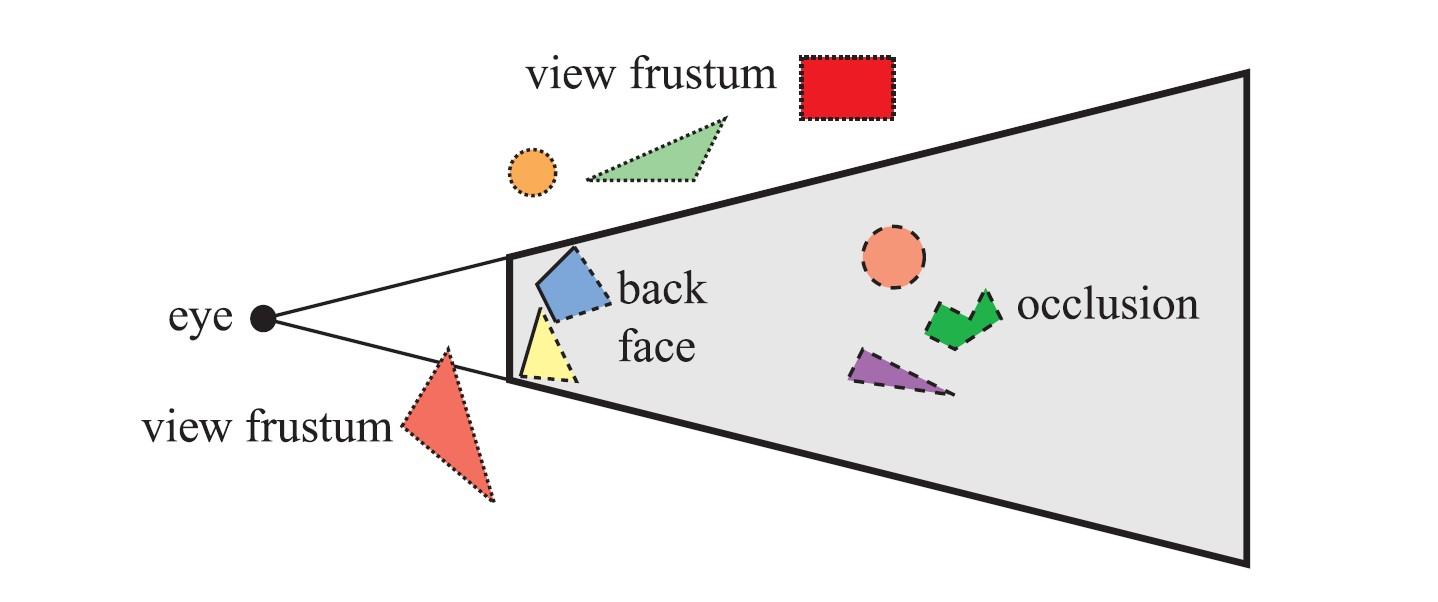
Plane Extraction in OpenGL
我们先从投影矩阵中提取Frustum平面,此时的模型视图矩阵是一个单位矩阵。
假设我们有一顶点 V:
$$
V=\left[ x ,y,z,w \right]^{T} (w = 1)
$$
矩阵M是一个4 x 4的投影矩阵:
$$
M=(m_{ij})
$$
V'是顶点V通过投影矩阵M变换的结果:
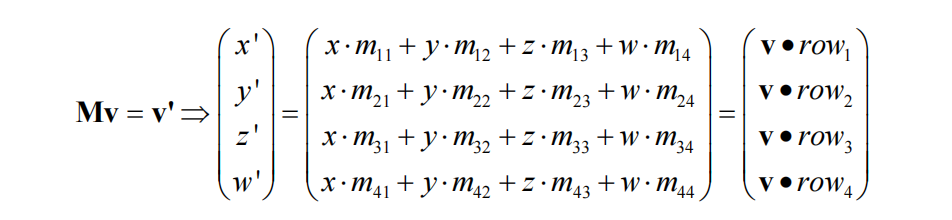
其中•表示点积, rowi表示矩阵M的第i行向量,如v·row2表示v与矩阵M的第二行所表示的向量的点积。
经过上述变换后,顶点V'将会处于齐次裁剪空间中。在这个空间,视图截锥就映射为了一个轴向对齐的Box。如果顶点V'在这个Box内,那么它必须满足以下条件:
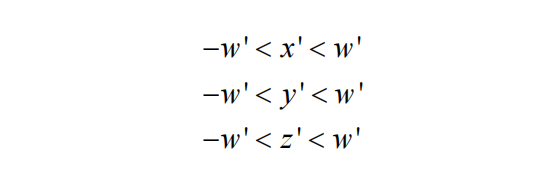
为什么需要满足以上条件?要怎么理解它?此时可能需要借助Projection Matrix:
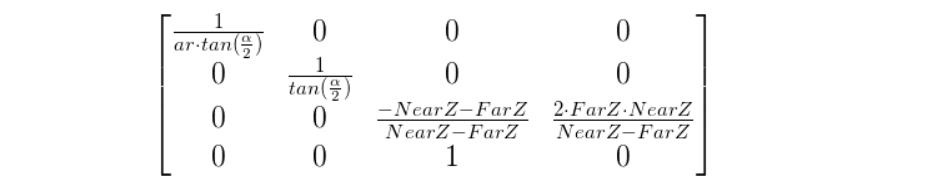
ar=width/height,代表屏幕宽高比
已知矩阵第四行第三列的值为1,这说明转换后顶点V'的w等于它的z值(即w'=z),在转为NDC空间过程需要通过透视除法除以它的w'值以让转换后的坐标点限制在[-1 1]的Box空间中,如果转换后的点不在该Box空间中,即剔除该点。以x'为例,当x'=w'时,x' / w' = 1,同理可证,要让转换后的点在NDC的[-1 1]空间中,就必须满足下述条件:
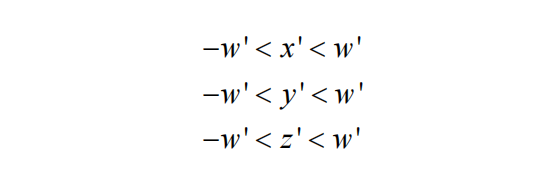
并且我们可以从上述不等式中得出一些结论,如下表:
| 条件 | 结论 |
|---|---|
| -w' < x' | x' 在左剪切平面的半内空间 |
| x' < w' | x' 在右剪切平面的半内空间 |
| -w' < y' | y' 在下剪切平面的半内空间 |
| y' < w' | y' 在上剪切平面的半内空间 |
| -w' < z' | z' 在近裁剪面的半内空间 |
| z' < w' | z' 在远裁剪面的半内空间 |
现在假设我们想测试一下x'是否在左剪切平面的半内空间中。如果以下不等式成立,也就是:
$$
-w' < x'
$$
结合开篇部分的信息,可以将不等式改写为:
$$
-(v \cdot row4) < (v \cdot row1)
$$
左右两边同时加上(v · row4),为:
$$
0 < (v \cdot row1)+(v \cdot row4)
$$
最后结果为:
$$
0 < v\cdot(row1 +row4)
$$
所以左裁剪平面的平面方程为:
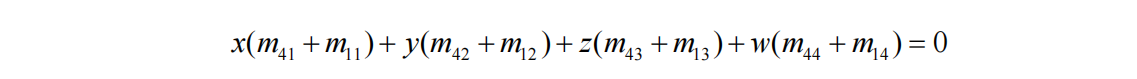
因为w等于1,所以可得:
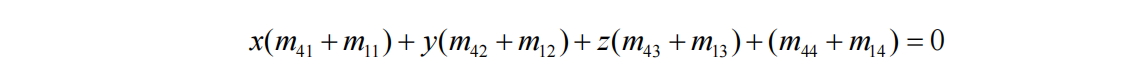
这就得到了平面的标准方程:
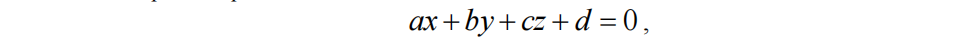
这里的:
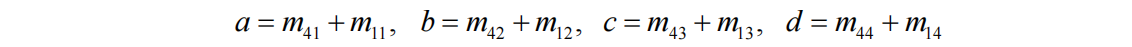
上述就是从投影矩阵中直接提取出视锥体左裁剪面的过程。值得注意的是,得到的平面方程没有归一化(即,平面的法向量不是单位向量),法向量指向内部的半空间。这意味着,如果顶点v在左裁剪平面的内部半空间中,则0 < ax + by + cz +d。
我们可以类似上述的求取过程得到所有裁剪平面:

Supporting a Non-Identity Modelview Matrix
上述我们假设模型视图矩阵是一个单位矩阵。然而,我们的目标是使算法对任意矩阵有效。这不是很难,稍微思考下,就很容易能够理解:
如果矩阵M是投影矩阵和模型视图矩阵的组合矩阵,则算法得出的结果就是模型空间中的裁剪平面(即M = V·P,其中V为模型视图矩阵,P为投影矩阵)。