SceneManagement实现

成熟的游戏引擎对SceneManagement的实现是必不可少的，同时SceneManagement涉及到的技术也复杂多样，场景排序，SceneManagement的八叉树实现，SceneCulling等都属于场景管理，本篇只对场景排序与FrustumCulling进行实现，八叉树实现与更复杂的遮挡剔除算法将在后续继续讨论。

使用SceneGraph可以很好地实现大量对象的高性能渲染。然而，我们仍然需要解决透明对象需要特定的渲染顺序的问题。此外，通常需要跳过对相机视角区域外的几何图形绘制——这种操作称为 FrustumCulling(截锥剔除)。在本篇中，将看到如何执行截锥剔除和几何排序，以及如何使用这种排序来提高渲染性能。

Node Order

Transparency

透明物体的渲染是需要确定好物体渲染先后顺序的，比如有两个对象:一个透明，另一个不透明，透明物体在物理上位于另一个物体的前面。如果先绘制不透明物体，alpha混合过程会得到正确结果，但如果先绘制透明物体，alpha混合会失败。理想情况下，透明的物体应该总是在其他非透明的物体之后绘制，并且应该按照从后到前的顺序绘制。也就是说，先绘制离相机最远的透明物体，然后绘制离相机较接近的透明物体，以此类推，直到最后绘制离相机最近的透明物体。这能够使alpha混合产生正确结果，并能渲染正确的几何画面。即使这不是完美的方案，因为透明物体仍然可能相交，要么与其它物体相交，甚至可能与自己相交。其实真正渲染透明物体的较完美的方法是在每个三角形的基础上进行渲染，但是对于游戏来说，将透明对象分开并从后向前绘制通常就足够了。

Overdraw

事实证明，对不透明物体进行排序也有好处。在正常渲染条件下，当网格中的顶点数据通过图形硬件管道时，片元着色器将在被几何体覆盖的逐个片元上执行。只有在片元着色器运行后才会执行深度测试，如果片元未通过深度测试，片元着色器的结果将被丢弃。

如果片元着色器只是使用简单的算法进行运算那还好，但是通常游戏中片元着色器的运算是复杂多变的，这就可能会造成严重浪费。我们可以把这种类型的浪费归类为Overdraw(过度绘制)现象的一部分：对于随机排序的各个不同物体的网格数据输入，重叠的物体将会导致最终屏幕像素会处理许多无用的片元。幸运的是，这两个问题都可以通过在渲染前对几何体进行排序来缓解，就像透明物体一样。但是，不同于透明物体从后往前对物体进行排序的方式，非透明物体的绘制是从前到后绘制，如果非透明物体依旧是从后往前绘制，反而会加剧Overdraw现象的发生。以这个简单的场景为例：

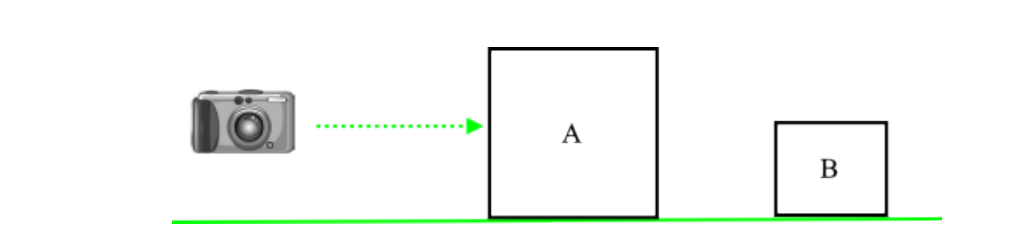
如果物体 B 在物体 A 之前绘制，则物体 B 的渲染进行的颜色和深度写入将被浪费，因为对象 A 完全挡住了对象 B。如果先绘制对象 A，则对象 B 的深度和颜色写入将会完全跳过，节省了不必要的操作带宽。从前到后渲染仍然会为每个像素多次执行片元着色器，但会降低内存带宽的消耗，作为一个表现良好、排序后的场景，这种排序带来的价值是巨大的，因为大场景中这种遮挡关系会更加频繁的发生，因此对图形内存的写入会大大的减少。

Early Z Test

传统渲染管线深度测试是在片元着色器后，但是实际上在光栅化阶段我们就能通过插值求取到每个片元的深度了，所以现代图形硬件在它的渲染管道中也提供了Early-Z阶段。这是一个深度测试组件，它放置在片元着色器之前，所以我们可以通过它避免无意义的片元着色器运算操作。只要满足一定的条件，潜在的片元可以在它们运行片元着色器之前被丢弃，从前到后的排序大大增加了Early-Z发生的机会。确切的条件取决于硬件，但通常禁用模板缓冲区和Alpha Test功能将会使Early-Z功能生效。它只是图形硬件中的一个组件，没有API状态专门启用或禁用Early-Z测试，所以其只会在适当的情况下自动发生。这也意味着很难测试Early-Z是否真的发生了，但由于从前到后渲染具有避免Overdraw的好处，尝试利用Early-Z也没有坏处。

Frustum Culling

在渲染网格顶点数据时，真正呈现画面区域的只是相机视角范围内的物体，而相机范围外的物体并不需要进行渲染，但是现实情况往往是不管物体有没有在相机视角范围内，都会对网格顶点数据提交渲染，这也大大增加了硬件内存的开销，针对该问题，它的解决方案是通过FrustumCulling(截锥剔除)进行优化。

Frustum(截锥)类似四棱台，正交投影会产生长方体截锥，透视投影将产生四棱台截锥。以透视投影四棱台为例，四棱台内的物体是当前相机视角范围内能被呈现画面的所有几何形体，四棱台的形状取决于相机的投影类型(vertical and horizontal field of vision)。投影矩阵中使用的near和far值将形成截锥的前面与后面。

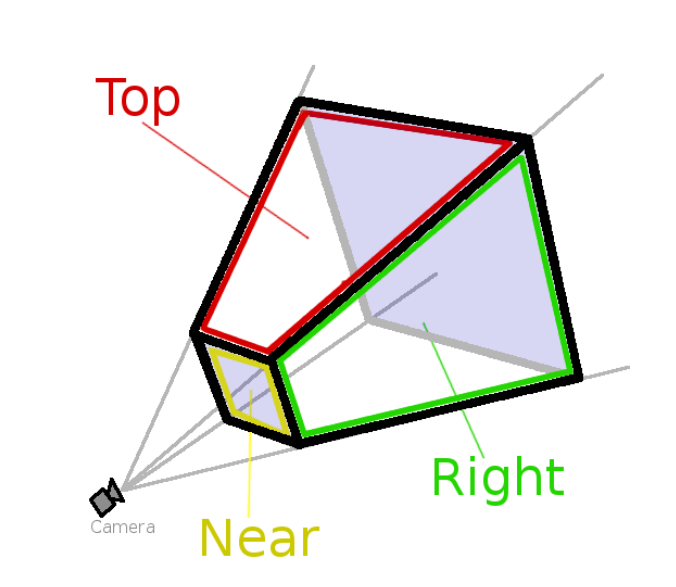
Bounding Volumes

为了有效地测试一个物体是否在Frustum中，通常测试其几何形状的包围体积。这是一个简单的形状，比如一个立方体或一个球体，它完全包围一个物体(类似于截锥完全包围了摄像机能看到的一切一样)。因此，可以执行少量的简单计算，而不用通过测试模型网格每个顶点是否在Frustum内。

通过立方体或球体等类似包围体并不能与场景中绘制的物体的形状完全一致，但只要这些包围体完全包裹着物体，它们就会在截锥剔除中发挥重要作用。虽然有时候一个物体可能会在它没有真正出现在屏幕上时就提交顶点数据(在上面的例子中，怪物手臂下面有很多空白空间，此时如果怪物已经在截锥体之外，但是立方体的空白区域还在Frustum内，还是会提交怪物的顶点数据)，但是执行截锥剔除通常会使整体的渲染性能得到很大提高。

Culling Equations

Frustum的截锥是由六个平面组成，平面的方程如下：

$$
ax+by+cz+D = 0
$$

这里的(a, b, c)为平面的法向量(不一定为单位向量)，(x, y, z)为平面上的点，D是将平面平移到坐标原点所需距离(所以D=0时，平面过原点)。

因为截锥剔除的作用是判断物体是否在截锥内，所以需要求取平面外的点到平面的距离。

我们可以求取下，已知平面外有一点Q(x0, y0, z0)，P(x, y, z)为平面上的点，求Q点到平面的垂直距离d：

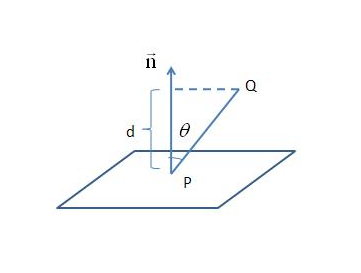过P做平面的法向量:

由图可知PQ在法向量n上的投影长度即为点Q到平面的距离d:

$$
d= \frac{\bar{n}}{|\bar{n}|}\cdot\bar{PQ} = \frac{\bar{n}\cdot\bar{PQ}}{|\bar{n}|}
$$

因为PQ向量的值为:

$$
\bar{PQ} = (x0 - x, y0 - y, z0 - z)
$$

所以：

$$
d = \frac{\bar{n}\cdot\bar{PQ}}{|\bar{n}|} = \frac{a(x0 - x) +b(y0 - y) + c(z0 - z)}{\sqrt{a^{2} + b^{2} + c^{2}}}
$$

继续展开:

$$
d = \frac{a(x0 - x) +b(y0 - y) + c(z0 - z)}{\sqrt{a^{2} + b^{2} + c^{2}}} = \frac{ax0 + by0 + cz0 - (ax + by + cz)}{\sqrt{a^{2} + b^{2} + c^{2}}}
$$

又因为ax + by + cz = -D，所以:

$$
d = \frac{ax0 + by0 + cz0 + D}{\sqrt{a^{2} + b^{2} + c^{2}}}
$$

如果法向量是单位向量，上面的分母部分就为1，所以最好确保法向量为单位向量，注意: 这里的d是有符号距离，不需要加绝对值；另外我们可以求取平面到原点的距离，此时(x0, y0, z0)可以用原点(0, 0, 0)代入, 此时原点到平面的距离就为：

$$
d = \frac{D}{\sqrt{a^{2} + b^{2} + c^{2}}}
$$

当法向量为单位向量，平面到原点的距离d=D。

我们可以把上面求证的结果稍微改写一下，变得更简单:

$$
(N \cdot V) + D = d
$$

其中N是法向量(a, b, c)并且为单位向量，V是平面外的参考点(x0, y0, z0)，(N · V)表示两个向量的点积, d为参考点到平面的距离。

上述方程的结果是参考点V到平面的距离d，以法线指向的一侧为平面前面的话，如果距离是负的，那么点在平面后面，如果是正的，那么点在平面前面。通过检验距离是否小于球面的负半径长度(为什么是负半径长度?如果物体中心在平面内(前),那么半径不管多大都可以判定为物体在平面内，此时物体到平面的距离必然大于负半径长度，因为距离是正的。如果物体中心不在平面内，只有当半径的长度大于物体中心到平面的无符号距离，才可以判定物体在平面内，此时物体中心到平面的距离小于负半径长度，因为距离是负的。所以可以总结为当物体中心到平面的距离大于负半径长度时，物体在平面内)，可以很容易地将这个方程展开来检验球面是否在平面内。

因此，我们可以简单地通过比较每个平面的点积和加法的结果来决定是否跳过当前物体的绘制来剔除网格，而不是在可能对最终可见场景没有贡献的巨大网格上执行顶点着色器操作。

Deriving a Frustum

OK，上述就是Frustum的介绍，Frustum一般用于对场景进行Culling(剔除)操作，但是它是如何做到的，以及如何生成一个Frustum？为了生成视锥体的 6 个面，我们可以从一个矩阵中导出它们(通过将当前投影矩阵乘以当前视图矩阵所形成的结果)。视图矩阵需要在笛卡尔空间中设置位置和方向，而投影矩阵需要根据投影矩阵的垂直视场设置近平面和远平面位置以及其它平面的角度。一旦我们有了该矩阵的结果，我们就可以从每一行中提取每个平面的轴，每一行的第四个值是该点到原点的距离。

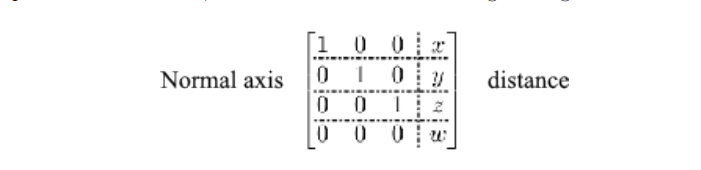
那么求取平面法线即可以通过下述方式(以左右平面为例)：

$$
Left Plane Normal = w axis + x axis
$$

$$
LeftPlaneDistance = w distance + x distance
$$

$$
Right Plane Normal = w axis - x axis
$$

$$
RightPlaneDistance = w distance - x distance
$$

最后求取的平面法线需要归一化。

Example

我们将创建一个场景，通过遍历场景节点，并将节点分成不透明与透明物体。然后根据它们与视图原点的距离对它们进行排序。然后，我们可以从前到后的顺序绘制不透明物体，以利用EarlyZ测试，然后从后到前的顺序绘制透明物体，以产生正确的alpha颜色混合效果。为了更好的优化场景，我们将添加Frustum Culling，并使用简单的球体半径检查-这对我们场景中的立方体并不完美，但是也能足够好地展示Frustum Culling功能。我们需要创建两个新的类型，Frustum与Plane类。此外需要对SceneNode进行补充：

public: 
        // 获取边界球体的半径
	inline float GetBoundingRadius() const { return boundingRadius; }
	// 设置边界球体的半径
	inline void SetBoundingRadius(float f) { boundingRadius = f; }
	// 获取当前物体到相机的距离
	inline float GetCameraDistance() const { return distanceFromCamera; }
	// 设置与相机的距离
	inline void SetCameraDistance(float f) { distanceFromCamera = f; }
	// 对比两节点到相机的距离
	static bool CompareByCameraDistance(SceneNode * a, SceneNode * b) {
		return (a -> distanceFromCamera <
			b -> distanceFromCamera) ? true : false;
	}
protected:
	float distanceFromCamera{0.0f};
	float boundingRadius{1.0f};

我们为SceneNode添加了几个新的成员变量，以及访问函数。为了执行Frustum Culling，还需要额外的代码来测试物体是否在Frustum内(为每个物体添加边界球体，实际开发一般会选择AABB进行，总体运行效率AABB>Sphere>OBB，OBB无疑是最契合物体的，但是很多时候不是空间换时间，就是时间换空间，而AABB是较为折衷的方案，后续可以新开文章讨论)。同时为了对SceneNodes排序，我们需要存储它们到相机的距离。还定义了一个静态函数来对不同物体到相机的距离进行比较。

#pragma once
#include "Vector3.h"
class Plane {
public:
	Plane(void) = default;
	Plane(const Vector3 &normal, float distance, bool normalise = false);
	~Plane(void) = default;

	void SetNormal(const Vector3 & normal) { this - > normal = normal; }
	Vector3 GetNormal() const { return normal; }

	void SetDistance(float dist) { distance = dist; }
	float GetDistance() const { return distance; }

	// 判断球体是否在平面内（前方）
	bool SphereInPlane(const Vector3 & position, float radius) const;

protected:
	// 平面法线
	Vector3 normal;
	// 平面延法线方向到原点的有符号距离
	float distance;
};

Plane类的代码比较简单明了，没什么可以解释的，下面是Plane类的cpp实现：

#include "Plane.h"
Plane::Plane(const Vector3 & normal, float distance, bool normalise) {
	// 如果需要归一化，则把normal与distance同时除以它自身的长度
	if (normalise) {
		float length = sqrt(Vector3::Dot(normal, normal));
		this -> normal = normal / length;
		this -> distance = distance / length;

	}
	else {
		this -> normal = normal;
		this -> distance = distance;
	}
}

bool Plane::SphereInPlane(const Vector3 & position,
	float radius) const {
        // 当距离小于负半径长度时，物体不在平面内
	if (Vector3::Dot(position, normal) + distance <= -radius) {
		return false;
	}
	return true;
}

我们的Frustum类也不是很复杂。它由6个Plane组成。我们需要一个公共函数来从矩阵中生成Frustum，以及一个公共函数来确定我们的场景节点是否在Frustum中。

#pragma once
#include "Plane.h" 
#include "SceneNode.h"
class Matrix4;
class Frustum {
public:
	Frustum(void) = default;
	~Frustum(void) = default;
        // 通过mvp矩阵生成6个Frustum平面
	void FromMatrix(const Matrix4 & mvp);
        // 判断节点是否在平面内
	bool InsideFrustum(SceneNode & n);
protected:
	Plane planes[6];
};

为了确定场景节点是否在Frustum中，我们使用了函数InsideFrustum。在我们简单的SceneNode系统中，我们将假设所有东西都包含在球体中，所以我们可以简单地针对组成Frustum的6个平面中的每一个做一次平面内是否包含球体的检查。如果场景节点的边界球在Frustum平面的外面，它就不能被看到，所以应该被丢弃。只有当它在所有平面内时，才应该绘制出来。

#include "Frustum.h"
#include "Matrix4.h"
bool Frustum :: InsideFrustum (SceneNode &n) {
  for( int p = 0; p < 6; ++ p ) {
      if (!planes[p].SphereInPlane(n.GetWorldTransform().
          GetPositionVector(), n.GetBoundingRadius())) {
               // 场景节点在Frustum外
               return false;
      }
  }
  // 场景节点在Frustum内
  return true ; 
}

接下来需要从ViewProjection矩阵中提取出Frustum 6个平面的结果：

void Frustum::FromMatrix(const Matrix4& mat) {
    Vector3 xaxis = Vector3(mat.values[0], mat.values[4], mat.values[8]);
    Vector3 yaxis = Vector3(mat.values[1], mat.values[5], mat.values[9]);
    Vector3 zaxis = Vector3(mat.values[2], mat.values[6], mat.values[10]);
    Vector3 waxis = Vector3(mat.values[3], mat.values[7], mat.values[11]);
  
    // RIGHT
    planes[0] = Plane(waxis - xaxis,
        (mat.values[15] - mat.values[12]), true);
    // LEFT
    planes[1] = Plane(waxis + xaxis,
        (mat.values[15] + mat.values[12]), true);
    // BOTTOM
    planes[2] = Plane(waxis + yaxis,
        (mat.values[15] + mat.values[13]), true);
    // TOP
    planes[3] = Plane(waxis - yaxis,
        (mat.values[15] - mat.values[13]), true);
    // FAR
    planes[4] = Plane(waxis - zaxis,
        (mat.values[15] - mat.values[14]), true);
    // NEAR
    planes[5] = Plane(waxis + zaxis,
        (mat.values[15] + mat.values[14]), true);
}

我们改造CubeRobot，为立方体机器人添加边界球：

CubeRobot::CubeRobot(): SceneNode(nullptr) {
    body -> SetBoundingRadius(15.0f);
    head -> SetBoundingRadius(5.0f);

    leftArm -> SetBoundingRadius(18.0f);
    rightArm -> SetBoundingRadius(18.0f);

    leftLeg -> SetBoundingRadius(18.0f);
    rightLeg -> SetBoundingRadius(18.0f);
}

为了验证Fustum Culling和不透明/透明节点的排序与渲染，我们需要稍微改变一下Renderer类。

#pragma once
class Renderer
{
public:
	Renderer(Window& parent);
	virtual ~Renderer();

	virtual void UpdateScene(float msec);
	virtual void RenderScene();

protected:
	void BuildNodeLists(SceneNode* from);
	void SortNodeLists();
	void ClearNodeLists();
        void DrawNodes ();
	void DrawNode(SceneNode*);

	SceneNode* root{nullptr};
	Camera* camera{nullptr};
	Mesh* quad;

	Frustum frameFrustum;
	vector<SceneNode*> transparentNodeList;
	vector<SceneNode*> nodeList;
};

我们需要三个新的Protected成员变量，一个Frustum与两个std::vectors用来存储不透明和透明的场景节点。除了我们在SceneGraph中创建的DrawNode函数，我们还需要4个新函数，它们都与SceneNodes的列表相关。每一帧，我们将执行以下的循环操作:

1)通过根节点的Update函数更新SceneGraph。

2)剔除Frustum区域外的节点，并使用BuildNodeLists函数将其放入对应的std::vectors列表中。

3)在SortNodeLists函数中，根据透明/不透明节点列表计算到摄像机的距离并对它们进行排序。

4)通过DrawNodes函数绘制不透明节点，然后是透明节点。

5)使用ClearNodeLists清除透明/不透明节点列表。

#include "Renderer.h"

Renderer::Renderer(Window& parent) : OGLRenderer(parent) {
	CubeRobot :: CreateCube ();
	projMatrix = Matrix4 :: Perspective (1.0f, 10000.0f,
	(float)width / (float)height, 45.0f);

	camera = new Camera ();
	camera -> SetPosition(Vector3(0 ,100 ,750.0f));

	 currentShader = new Shader ("SceneVertex.glsl",
	 "SceneFragment.glsl");

	 quad = Mesh::GenerateQuad();
	 quad -> SetTexture(loadTexture(
	   "stainedglass.tga", 1, 0, 0));

	 if (!currentShader->LinkProgram () || !quad ->GetTexture()) {
		return;
	 }
	 root = new SceneNode();
	 // 添加5个透明面片
	 for (int i = 0; i < 5; ++i) {
		 SceneNode * s = new SceneNode();
		 s -> SetColour(Vector4(1.0f, 1.0f, 1.0f, 0.5f));
		 s -> SetTransform(Matrix4::Translation(
		 Vector3(0, 100.0f, -300.0f + 100.0f + 100 * i)));
		 s -> SetModelScale(Vector3(100.0f, 100.0f, 100.0f));
		 s -> SetBoundingRadius(100.0f);
		 s -> SetMesh(quad);
		 root -> AddChild(s);
	 }
	 root -> AddChild(new CubeRobot());
	 glEnable(GL_DEPTH_TEST);
	 glEnable(GL_BLEND);
	 glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
	 init = true;
}

Renderer::~Renderer() {
	// 清理场景节点
	delete root;
	delete quad;
	delete camera;
	// 清理cube mesh
	CubeRobot::DeleteCube();
}

void Renderer::UpdateScene(float msec) {
	camera->UpdateCamera(msec);
	viewMatrix = camera->BuildViewMatrix();
	frameFrustum.FromMatrix(projMatrix * viewMatrix);
	// 更新所有节点的worldTransform
	root->Update(msec);
}

void Renderer::BuildNodeLists(SceneNode * from) {
	if (frameFrustum.InsideFrustum(*from)) {
		Vector3 dir = from -> GetWorldTransform().GetPositionVector() -
		camera -> GetPosition();
		from -> SetCameraDistance(Vector3::Dot(dir, dir));
		// 当节点带透明度时，把它加入透明列表中
		if (from -> GetColour().w < 1.0f) {
			transparentNodeList.push_back(from);
		}
		else {
			// 当节点时非透明时，加入非透明列表中
			nodeList.push_back(from);
		}
	}
	for (auto* node: from->GetChildren()) {
		BuildNodeLists(node);
	}
}

void Renderer::SortNodeLists() {
	// 虽然我们对透明物体与非透明物体都使用相同的排序，但是在绘制时透明物体会反向绘制
	std::sort(transparentNodeList.begin(),
		transparentNodeList.end(),
		SceneNode::CompareByCameraDistance);
	std::sort(nodeList.begin(),
		nodeList.end(),
		SceneNode::CompareByCameraDistance);
}

void Renderer::DrawNodes() {
	for (auto* node : nodeList) {
		DrawNode(node);
	}
	// 对透明物体反向绘制(即由远到近绘制)
	for (vector < SceneNode* >::const_reverse_iterator i =
		transparentNodeList.rbegin();
		i != transparentNodeList.rend(); ++i) {
		DrawNode((*i));
	}
}

void Renderer::ClearNodeLists() {
	transparentNodeList.clear();
	nodeList.clear();
}

void Renderer::RenderScene() {
	BuildNodeLists(root);
	SortNodeLists();
	glClear(GL_DEPTH_BUFFER_BIT | GL_COLOR_BUFFER_BIT);

	glUseProgram(currentShader->GetProgram());
	UpdateShaderMatrices();

	glUniform1i(glGetUniformLocation(currentShader->GetProgram(),
			"diffuseTex"), 0);
	// 绘制画面
	DrawNodes();

	glUseProgram(0);
	SwapBuffers();
	// 需要清空节点，以便下一帧重新计算
	ClearNodeLists();
}

void Renderer::DrawNode(SceneNode * n) {
	if (n->GetMesh()) {
		Matrix4 transform = n->GetWorldTransform() *
		Matrix4::Scale(n->GetModelScale());
		glUniformMatrix4fv(
			glGetUniformLocation(currentShader -> GetProgram(),
				"modelMatrix"), 1, false, (float*)&transform);

		glUniform4fv(glGetUniformLocation(currentShader -> GetProgram(),
				"nodeColour"), 1, (float*)&n -> GetColour());

		glUniform1i(glGetUniformLocation(currentShader -> GetProgram(),
				"useTexture"), (int)n -> GetMesh() -> GetTexture());
		// 绘制mesh
		n->Draw(*this);
	}
}

我们的main函数如下：

int main() {
	Window w("Scene Management!", 800,600,false);
	while(w.UpdateWindow() && !Window::GetKeyboard()->KeyDown(KEYBOARD_ESCAPE)){
		renderer.UpdateScene(w.GetTimer()->GetTimedMS());
		renderer.RenderScene();
	}
	return 0;
}

最后运行效果如下：