要求取二次误差矩阵,我们需要选择一个具有启发性的方法进行构建。我们选取的方法与下述链接给出的方法非常相似。
根据上述方法,我们可以通过观察了解到,在原始模型中,每一个顶点都是一组平面相交的解——即在对应顶点中有不同的三角面相交于该顶点。我们可以将顶点与相关平面集合产生关联,并将顶点相对于该平面集合的误差度量定义为到其所关联平面的距离的平方和:
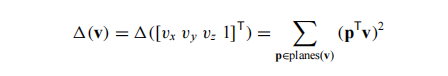
上述式子中,
$$
p = [a \space b \space c \space d]^{T}
$$
表示通过方程ax + by + cz + d = 0所定义的平面,其中a² + b² + c² = 1。
尽管我们在平面集合上使用了求和的方式而不是通过最大值的方法,但是▲v表示的误差度量还是与上述链接中所介绍的方法近似。而与顶点相交的所有三角面都会被当做平面集合的整体被初始化,需要注意的是,如果我们要像上面文档链接中那样明确的跟踪这些平面集合,那么我们会使用下述规则来坍缩(v1, v2) → v:
$$
planes(v) = planes(v1) ∪ planes(v2)
$$
它需要相当大的存储量,而且不会随着模型简化的进一步进行而减少。
我们可以对开篇的公式改写为如下形式:
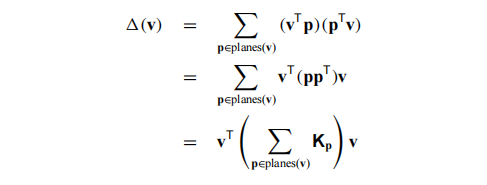
其中**Kp**的值为:
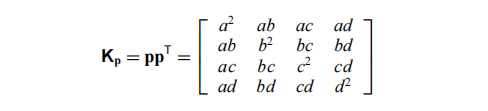
可以看到Kp是一个基本的二次误差曲面,用矩阵表示,它可用于求取空间中任意点到平面p的平方距离。我们可以将这些基本二次曲面相加,并用单个矩阵Q 来表示一整组平面。那么上述平面集合的并集 (planes(v1 ) ∪ planes(v2)) 就可以使用单个矩阵来隐式跟踪,并可以通过添加两个二次曲面 **(Q1 + Q2)**来表示它们的并集。但是,每个不同的平面最多可以 3 次计数,因为平面最初仅分布到其定义的三角面的顶点上。这可能会给误差测量带来一些不精确性,但它有很大的好处:跟踪一个平面集所需要的空间只是一个4×4的对称矩阵所需要的空间(10个浮点数),而更新误差测量的近似值成本只是增加两个这样的矩阵的成本而已。
我们对以下立方体进行分析:
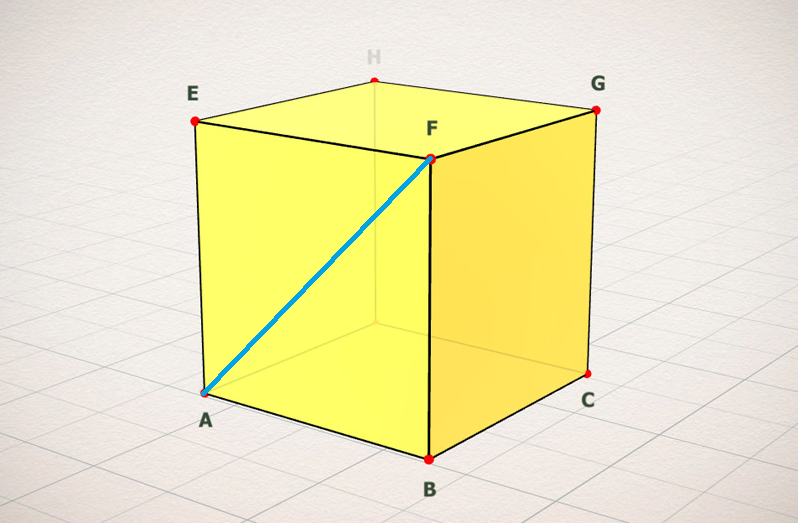
我们讨论的立方体或其它模型是使用共用顶点的方式(即通过索引缓冲区)建模。假定我们会迭代100次:
for (let iteration = 0; iteration < 100; iteration++) {
if (triCount - delTri <= targetCount) break;
// 每隔updateStep数值更新mesh
if (iteration % updateStep === 0) {
updateMesh(iteration, recompute);
}
......
}
在updateMesh函数中,我们会在第一次迭代以及recompute是否为true时为逐个顶点计算矩阵Q:
updateMesh(iteration, recompute) {
...
if (recompute || iteration === 0) {
for (i = 0; i < vertices.length; i++) {
vertices[i].q = new Quadric();
}
...
}
...
}
上篇我们说到矩阵Q是一个对称矩阵,只需要10个数值进行填充,所以我们创建了Float32Array并且确定它的长度为10:
class Quadric {
constructor() {
this.m = new Float32Array(10);
this.setZero();
}
setZero() {
for (let i = 0; i < 10; ++i) this.m[i] = 0;
}
addSelf (n) {
this.m[0]+=n.m[0]; this.m[1]+=n.m[1]; this.m[2]+=n.m[2]; this.m[3]+=n.m[3];
this.m[4]+=n.m[4]; this.m[5]+=n.m[5]; this.m[6]+=n.m[6]; this.m[7]+=n.m[7];
this.m[8]+=n.m[8]; this.m[9]+=n.m[9]
}
set( m11, m12, m13, m14, m22, m23, m24, m33, m34, m44 ) {
this.m[0] = m11;
this.m[1] = m12;
this.m[2] = m13;
this.m[3] = m14;
this.m[4] = m22;
this.m[5] = m23;
this.m[6] = m24;
this.m[7] = m33;
this.m[8] = m34;
this.m[9] = m44;
return this;
}
makePlane( a, b, c, d ) {
return this.set(
a * a, a * b, a * c, a * d,
b * b, b * c, b * d,
c * c, c * d,
d * d
);
}
...
}
接着updateMesh函数的逻辑,我们需要对矩阵Q进行实际填充,因为矩阵Q是通过各顶点形成的三角面的平面公式(ax + bx +cz +D = 0)进行构造,所以我们需要遍历三角面,并通过三角面的三个顶点求取出(a, b, c, D)的值,如下:
updateMesh(iteration, recompute) {
...
if (recompute || iteration === 0) {
...
for (i = 0; i < triangles.length; i++) {
let t = triangles[i],
// 通过三角面的索引找到三个顶点
/*
6---- 7
/| /|
2----3 |
| | | |
| 4--|-5
|/ |/
0----1
*/
p = t.indices.map(i => vertices[i].p),
p10 = vec3.subtract(p[1], p[0]),
p20 = vec3.subtract(p[2], p[0]),
// 叉乘后求取法线
n = vec3.cross(p10, p20),
q = new Quadric();
vec3.normalize(t.n, n);
// 因为法线是背离原点的,法线点乘于顶点可得该顶点到原点的垂直有符号距离
// 这边是不是取的p[0]不重要,只要是属于三角面上的任意顶点就行
q.makePlane(t.n[0], t.n[1], t.n[2], -vec3.dot(t.n, p[0]));
// 只要有共用顶点,涉及到的相关平面矩阵就得进行累加
for (j = 0; j < 3; j++) {
vertices[t.indices[j]].q.addSelf(q);
}
}
...
}
...
}
接着上面的逻辑,后面我们要计算误差度量值了:
updateMesh(iteration, recompute) {
...
if (recompute || iteration === 0) {
...
for (i = 0; i < triangles.length; i++) {
let t = triangles[i],
p = vec3.create(),
pts = t.indices.map(i => vertices[i]);
for (j = 0; j < 3; j++) {
let v1 = pts[j],
v2 = pts[(j + 1) % 3];
// 对关联顶点对[0][1],[1][2],[2][0]计算误差度量值
t.err[j] = calError(v1, v2, p);
}
// 取出最小的误差度量值在索引为3的位置
t.err[3] = Math.min(t.err[0], t.err[1], t.err[2]);
}
}
...
}
...
}
接着我们会使用误差度量所计算的结果在阈值的判断上:
let threshold = 0.000000001 * Math.pow(iteration + 3, 7);
for (i = triangles.length - 1; i >= 0; i--) {
let t = triangles[i];
if (t.err[3] >= threshold || t.deleted || t.dirty) continue;
for (j = 0; j < 3; j++) {
if (t.err[j] >= threshold) continue;
...
}
// 是否减面完成
if (triangle_count - deleted_triangles <= target_count) break;
}
输出结果(减面前):


减面后:

