概要
计算机图形学的许多应用需要复杂并高度细节化的模型,但是每个应用实际需要的细节化程度要求却可能大不相同。为了控制处理的时间成本,通常会使用模型近似来代替过度细节化的模型。
这篇会介绍如何通过模型表面简化算法来快速的生成高质量的模型近似。该算法使用顶点对的迭代坍缩来简化模型,并使用二次型矩阵(quadric matrices)维持表面误差近似值。通过收缩任意的顶点对(而不仅仅是边),我们的算法能够连接模型中不相连的区域。这可以促进更好的近似,无论是在视觉上还是在几何误差方面。为了允许拓扑连接,我们的系统还支持非流形曲面模型。
介绍
许多计算机图形应用程序需要复杂、高度细节的模型来突出令人信服的真实感。因此,通常以非常高的分辨率创建或获取模型,以适应这种高细节的需求。然而,有些模型并不需要太过复杂,并且模型的计算成本与其复杂性直接相关,因此就需要复杂模型的简单版本。当然,我们希望自动生成这些简化的模型。这就是为什么要推出曲面简化算法的目的。
与这一领域的大多数其他功能一样,我们将关注多边形模型的简化。我们将假设模型是由三角面构成。这并不意味着会失去通用性,因为原始模型中的各个多边形都可以作为预处理阶段的一部分进行三角化。为了获得更可靠的结果,当两个三角面的角相交于一点时,应将不同的两个面定义为共享一个顶点,而不是使用两个在空间上碰巧重合的独立顶点。
这篇文章讨论的算法,是基于顶点对的迭代坍缩。随着算法的进行,在当前模型的每个顶点上保持一个几何误差近似。这种误差近似用二次矩阵表示。算法的主要优点是:
效率:该算法能够非常快速地简化复杂模型。例如,我们的实现可以在70,000面的模型中简化至100面,并保持模型近似。
质量: 算法产生的近似保持了原始模型的高保真度。即使经过显著的简化,模型的主要特征也得以保留。
通用:与大多数其他模型简化算法不同,我们讨论的算法能够将模型不相连区域进行连接,我们将这一过程称之为聚集。假设不需要保持对象的拓扑结构,那么这可以促进对具有许多不相连的各部件模型进行更好的整合与近似。这也要求我们的算法支持非流型模型。
背景及相关工作
多边形曲面简化的目标是将一个多边形模型作为输入,并生成一个简化模型(即原始模型的近似模型)作为输出。我们假设输入模型(Mn)已经被三角化了,目标近似模型(Mg)将满足某些给定的标准,通常是期望的面数或最大可容忍误差。总之这些算法可以用于渲染系统的多分辨率建模——生成针对当前应用需要的具有适当细节级别的模型。
对于是否需要维持模型的拓扑结构,算法并不强制要求。根据应用领域的不同,例如医学成像,维持模型的拓扑结构可能是必要的。然而,在渲染等应用程序领域,是否保持拓扑结构无关于整体外观(即保留拓扑结构不如整体外观重要)。说了一堆干话,想说明的是我们讨论的算法既能保持拓扑结构,也能连接本互不相连的区域。
许多更早之前的简化算法或隐式或显式地假设它们的输入的模型曲面是(并且应该保持)流形曲面。让我们强调一下,我们并没有做这样的假设。事实上,聚合的过程会有规律性地产生非流形区域。
表面简化
近年来,模型曲面简化问题,以及更普遍的多分辨率建模问题,受到越来越多的关注。已有几种不同的算法用于简化曲面。大致可以分为三类:
顶点抽取(Vertex Decimation):
上述链接提供的方法通过迭代选择一个要删除的顶点,并删除所有相邻的面,删除后的顶点或面必然会造成模型缺失,最后会对模型缺失的部分重新通过算法生成三角面,以填补缺失的部分。
第二个链接描述了一个更复杂,但本质上与第一个链接是类似的算法。虽然两种算法提供了合理的效率和质量,但这些方法并不能完全满足我们的要求。这两种方法都使用了顶点分类和三角剖分的方案,而该方案都只能局限于流形曲面,并且它们都必须小心地维护模型的拓扑结构。虽然上面说到某些领域需要维护拓扑结构,但它们对多分辨率渲染系统有极大的限制。
顶点聚合(Vertex Clustering):
上述链接描述的算法是少数能够处理任意多边形输入的算法之一。在原始模型周围放置一个边界框,并将其划分为各个相间的网格。在每个网格单元中,网格单元的顶点聚在一起成为单个顶点,对应模型的面也要相应更新。这个过程可以非常快速,并且可以对模型的拓扑产生巨大的改变。然而,虽然网格单元的大小确实能提供一个几何误差界限,但输出的质量通常会产生廉价的既视感。此外,很难用特定的面数构造近似模型,因为面的数量是由指定的网格尺寸来间接决定的。产生的精确近似也依赖于原始模型相对于周围网格的实际位置和方向。这种方法也确实可以很容易地推广到使用自适应的网格数据结构,如
它依赖于八叉树。这可以提高简化结果,但仍然不能满足我们所期望的质量和简洁有效的控制。
迭代边缘坍缩:
目前已经发布了几种通过迭代边缘坍缩来简化模型的算法(如下图)。
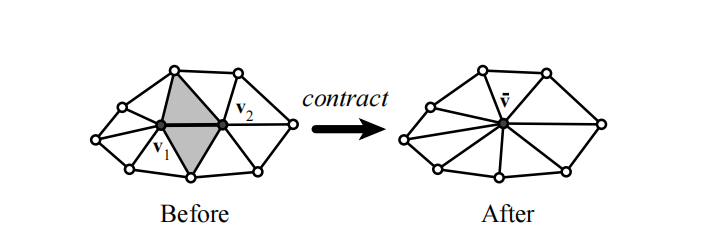
这些算法之间的本质区别在于它们如何选择坍缩边缘。此类算法有一些值得注意的例子是 :
这些算法基本上针对的是流形曲面,尽管边缘坍缩可以用于非流形曲面,但它们不能连接本不相连的区域。
上述已经发布的算法都没有提供我们期望的效率、质量和通用性的结果。顶点抽取算法不适合我们的需求;算法需要小心翼翼地维护模型拓扑关系,并且通常需要以流形曲面为处理前提。顶点聚合算法虽然比较通用并且效率也不错!但是,它们对结果的可控性比较差,而且这些结果的质量参差不齐。而边缘坍缩算法并不支持聚合。
我们要讨论的算法同时支持聚合和高质量的近似。它兼具顶点聚合的通用性,并且也能达到很好的质量和简洁的控制。它还比某些更高质量的算法有更快的简化能力(比如Progressive Meshes中介绍的方式)。
通过顶点对的坍缩
我们讨论的简化算法是基于顶点对的迭代坍缩,它是上述介绍的迭代边缘坍缩技术的扩展。假设我们有顶点v1与v2,它的工作原理就是把与顶点v2相连的所有边连接到顶点v1中,并去除顶点v2的过程。过程中除了顶点v2会被剔除外,任何与顶点v1与v2相关的边或面都有被剔除的可能。过程的影响结果很小并且也只对相关顶点周边产生局部影响,这将产生两种结果:
1.对本已经相连的Mesh进行简化,如下图:
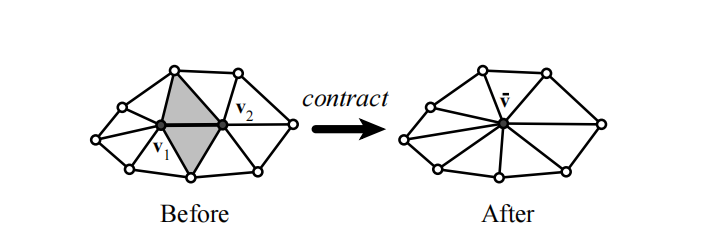
2.对本不相连的Mesh形成聚集:
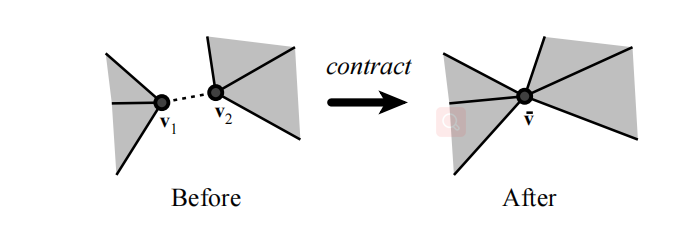
这种处理的方式实际上是很普遍的,我们可以把一组顶点集合(v1, v2, ..., vk)坍缩至单个顶点v。这种坍缩方式是个很广义的概念,既可以表示为成对的顶点坍缩,也可以表示为更一般性的坍缩方式,比如顶点聚合。但是我们还是采用顶点成对坍缩的方式作为我们算法的原子操作,因为它具有更细粒度的坍缩操作。
我们如果把最初的原始模型用Mn表示,当应用了一系列的顶点对坍缩算法进行迭代后,实际上就是对当前模型的表面进行增量修改,所以算法实际上会生成一系列的模型Mn,Mn-1,...,Mg;此时Mg就是原始模型的最简模型。因此,单次运行可以产生大量近似模型或多分辨率的不同模型表示,例如上面提到的Progressive Meshes。
Aggregation
利用顶点对坍缩算法的主要好处是算法能够将模型中从未连接的区域连接在一起(可减少drawcall)。但这也使算法对原始模型的网格的连接不那么敏感。如果模型的两个面有重合的顶点,那么顶点的坍缩将修复初始网格模型的这个缺陷。
上面说到,在渲染领域网格的拓扑结构可能不如整体形状重要。如下图,它由规则的100个紧密相连的立方体组成。假设我们想要构建左侧100个立方体模型的近似值,以便在一定距离上进行渲染(如LOD)。基于边缘坍缩的算法注定了它无法连接不相连的各个立方体,并且随着迭代的进行镂空的区域会越来越大(下图中间部分)。而使用顶点对坍缩算法,不相连的模型或网格可以合并成一个单独的模型对象,如下图右侧的画面所示,它的结果将会是一个更加可靠的近似。
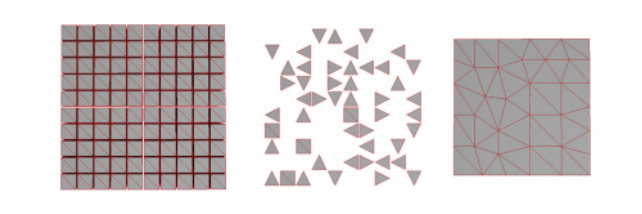
Pair Selection
我们会在初始化时选择有效的顶点对,并在应用算法过程中只考虑这些顶点对。过程需要基于这样的假设:即在一个很好的近似下,顶点不会远离它们在模型中的原始位置(这样模型才不会严重变形)。
当满足下面条件之一时,可以认为顶点(v1, v2)是有效顶点对:
- (v1,v2)两顶点形成三角面的边缘;
- 或 |v1 - v2| < t, 其中t是我们指定的阈值;
当阈值 t = 0 时,会剔除重合的顶点,它是简单的边缘坍缩算法。较高的阈值会使得不连接的顶点配对。所以阈值的设置就显得很重要。因为如果太高,模型互相远离的顶点可能会被连接,这当然是不可取的,并且它可能会创建 O(n²) 对。
在迭代坍缩的过程中,我们必须跟踪顶点有效对的集合。对于顶点对中的顶点,我们会将其作为成员的配对集合联系起来。当我们坍缩(v1, v2 )→ v 时,v1不仅会取得所有与v2相连的边,而且还会将与v2的配对集合合并到v1自己的集合中。在所有的有效配对过程中,v2的每一次出现都会被v1所取代,重复的配对也会被剔除。
Approximating Error With Quadrics
为了在应用迭代算法中选择要执行的坍缩,我们需要考虑坍缩的计算方法及目标顶点到原始顶点的误差▲v。为此我们将定义一个4x4矩阵Q,它会与每个顶点结合,并将顶点v(指的是源顶点,后面会说到如何找到该点):
$$
v=[v_{x} v_{y} v_{z} 1]^{T}
$$
通过矩阵Q,计算出▲v:
$$
\Delta v = v^{T}Qv
$$
后面我们会介绍如何构造初始矩阵Q.注意:
$$
\Delta v=\varepsilon
$$
是针对所有顶点的集合,它相对于Q的误差为∑,并且它是一个二次曲面.
为了执行坍缩(v1,v2)→ v,这一个过程有不同的算法可以完成映射. 简单的方法是直接选择v1、v2点或通过(v1 + v2 )/2来取v1与v2的中点位置,这取决于其中哪一个位置能产生▲v的最小值。然而,由于误差函数▲v是二次的,所以找到其最小值是一个线性问题。因此,我们通过解决∂▲/∂x = ∂▲/∂y = ∂▲/∂z = 0来找到v:
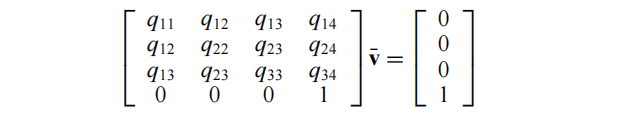
因为矩阵的最下面一行是(0, 0, 0, 1),而结果也是(0, 0, 0, 1), 所以v 的 w 分量也是 1。假设这个矩阵是可逆的,我们可以得到:
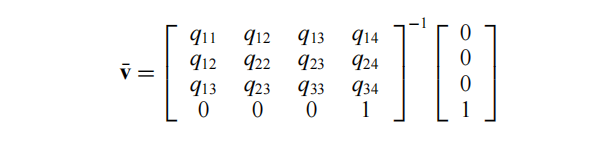
如果这个矩阵不是可逆的,我们就试图沿着v1 v2所形成的线段中找到最优顶点。如果这也失败了,我们就会选择从两端点或中点中选择v。
Algorithm Summary
我们的简化算法是围绕顶点对坍缩和误差二次曲线构建的。当前的实现使用邻接图结构来表示模型:顶点、边和面都明确表示并关联在一起。为了跟踪有效顶点对的集合,每个顶点都维护一个它所属的顶点对的列表。算法本身可以快速总结如下:
1.计算所有源顶点的Q矩阵。
2.选择所有有效的顶点对。
3.通过下述公式,得出每个有效顶点对的最优坍缩点
$$
\Delta v = v^{T}Qv
$$
4.将所有对放在一个以误差度量值▲v为键的堆中,最小成本对位于该堆的顶部。
5.迭代地从堆中移除误差度量值最小的顶点对 (v1, v2 ),坍缩该顶点对,并更新所有与 v1 有关联的有效顶点对的误差度量值。
剩下的唯一问题是如何计算初始矩阵Q,并从中构建误差度量值▲v。
算法原作者: Michael Garland,Pail S.Heckbert