在 Transformation Matrix 变换矩阵(二) 中已经知道LookAt矩阵的原理与实现,但是实际开发中可能不会直接采用LookAt矩阵进行相机视图的空间变换,并且相机视图空间为什么要进行所谓的逆操作也需要更加明确。
相机空间为什么要进行逆操作?
假设模型矩阵为M,视图矩阵为V, 得出的结果矩阵为R, 那么公式如下:
$$
V∗M=R
$$
假设相机在世界空间原点位置,模型在z=-10位置,以实际矩阵值代入V,M,R中,如下:
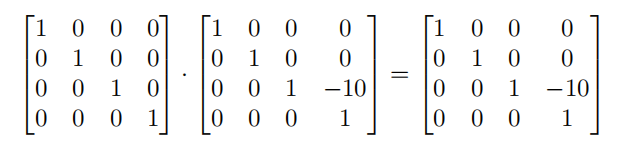
因为此时相机的视图矩阵是单位矩阵,所以转换的结果很容易就能计算,但是如果相机与模型都在x为10的位置上呢?
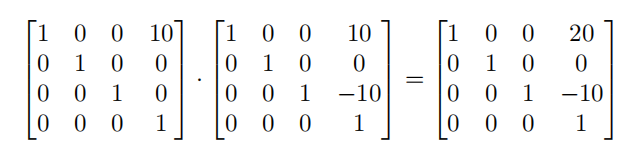
得出的结果x=20,这看起来不太对,如果我们使用这个矩阵来渲染我们的对象,它会出现在屏幕的右侧,而它应该仍然在屏幕中心,因为立方体和摄像机都在x轴以相同的数量移动。
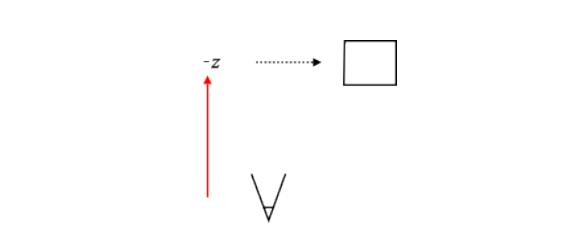
所以我们应该让视图矩阵V以相反方向移动10个单位,让它回到原点进行渲染,得出的结果如下:
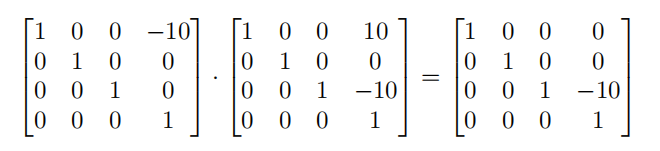
此时模型就回到屏幕中心位置了,还是不太理解?为了更容易理解,我们可以让相机位置在x=5的位置,让模型还是在x=10的位置,此时在屏幕中呈现的图像应该在中心偏右5个单位的位置(我们的分析忽略z的值):
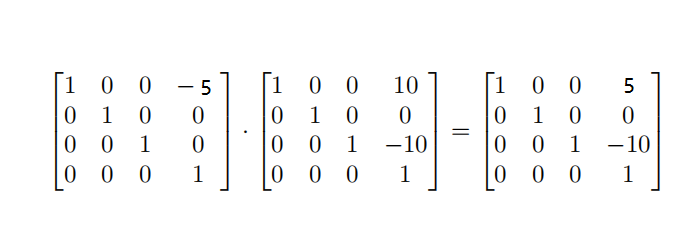
上面的分析针对的是位移间的转换关系,那么旋转呢?其实旋转也是类似,为了便于说明,这里以2D旋转为例,假设V是旋转矩阵,此时M为模型位置点且坐标为(1, 0):
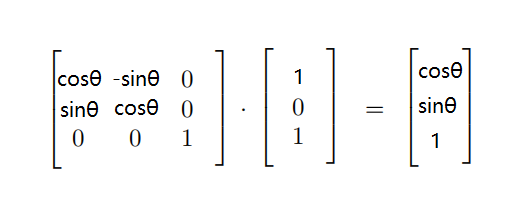
假设V旋转了30°,则变换后的模型位置点变为了(sqrt(3)/2,1/2) ,但是实际上此时M点在旋转空间的位置如下:
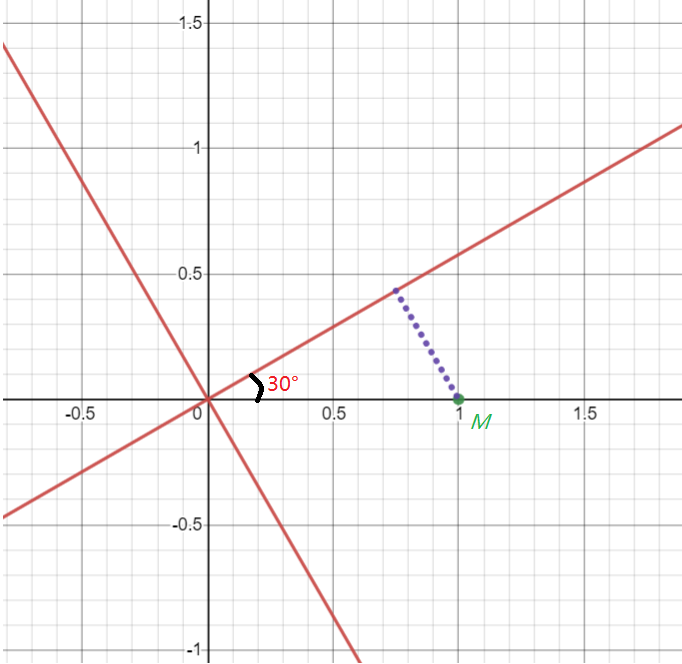
上图红线所形成的坐标系是旋转后形成的旋转空间,此时在该旋转空间下M的位置应为 (sqrt(3)/2,−1/2) ,而不是 (sqrt(3)/2,1/2) ,而旋转空间如果求取为之前矩阵的逆矩阵,如下:
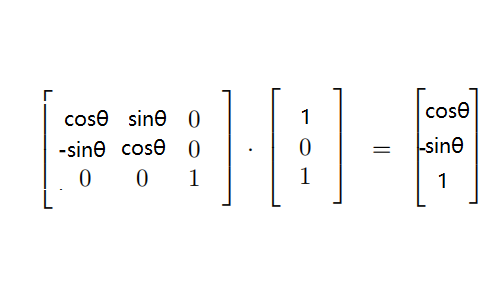
代入30°,则结果正好为(sqrt(3)/2,−1/2) 。
所以一般在代码中求取视图矩阵都会求取其“逆”过程,用于定位点在变换后所在空间的位置。
Matrix4 Camera::BuildViewMatrix(){
return Matrix4::Rotation(-pitch, Vector3(1,0,0)) *
Matrix4::Rotation(-yaw, Vector3(0,1,0)) *
Matrix4::Translation(-position);
};
总结:假设原矩阵为A,它的逆矩阵为B,则逆矩阵B与顶点v相乘的结果就是把v在以原矩阵A为坐标系下重新标注的结果。