随机与噪声系列会对以下噪声进行实践,包括了White Noise, Value Noise, Layered Noise,Voronoi Noise以及Tiling Noise。下面进入White Noise部分。

要开始noise部分必然要先知道随机的概念,实际上Noise的生成就是通过各个部分的不确定性而输出的最后结果,如何在看似可预测的代码环境中来确保随机性是我们要讨论的重点。
很多复杂的效果必然先从简单的效果着手进行分析,先在一维的环境分析下如何生成随机值。
1D随机
我们讨论的所有Noise都是为了图片效果输出服务,而着色器颜色值的输出数值结果范围在01之间,我们很容易能想到是否可以运用fract函数来生成随机值 (可参阅Shader实验室:fract函数),因为fract函数的生成结果也在01之间:
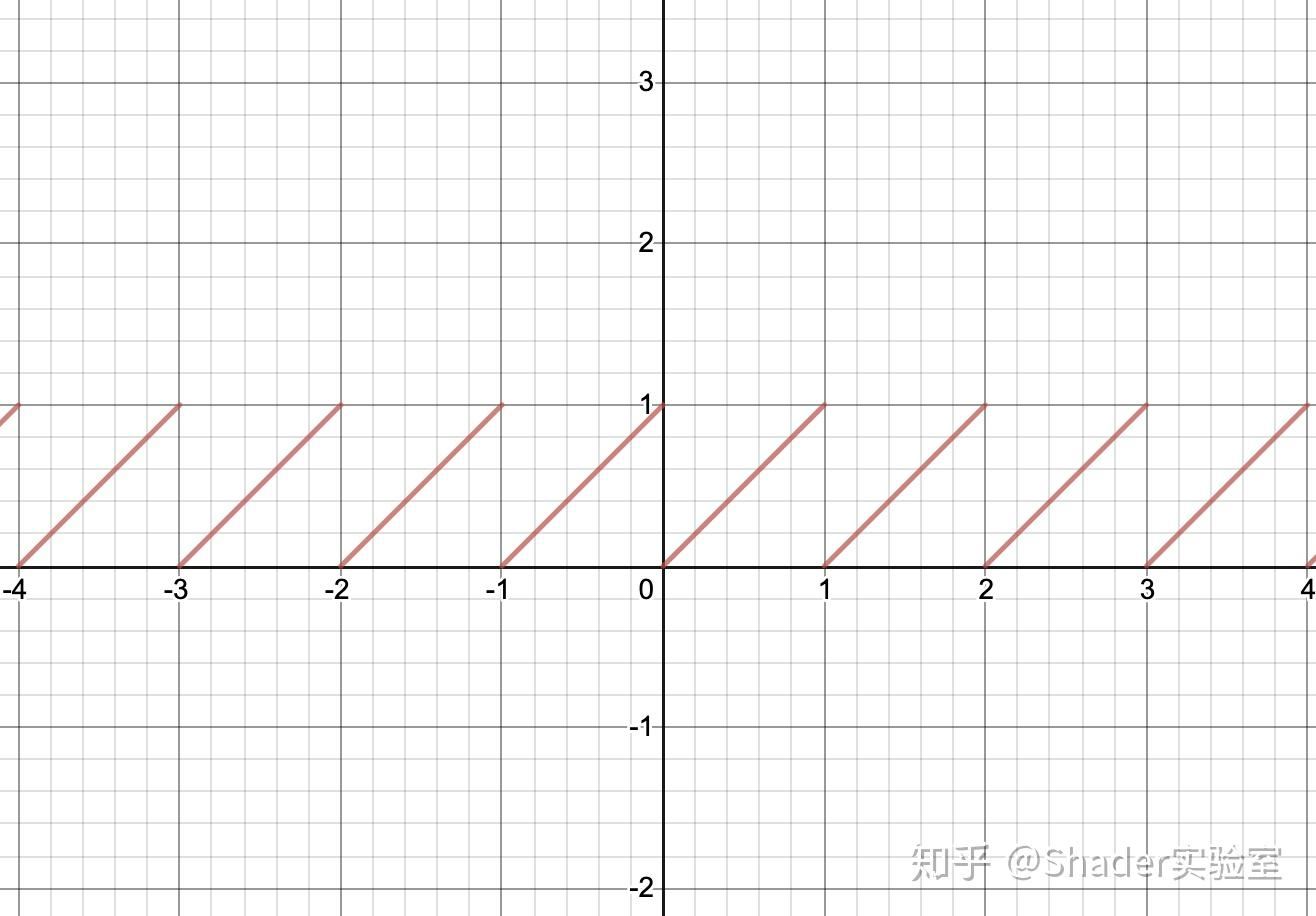
fract(x)的计算结果肯定还无法满足随机的条件,那乘于10乃至1000呢?
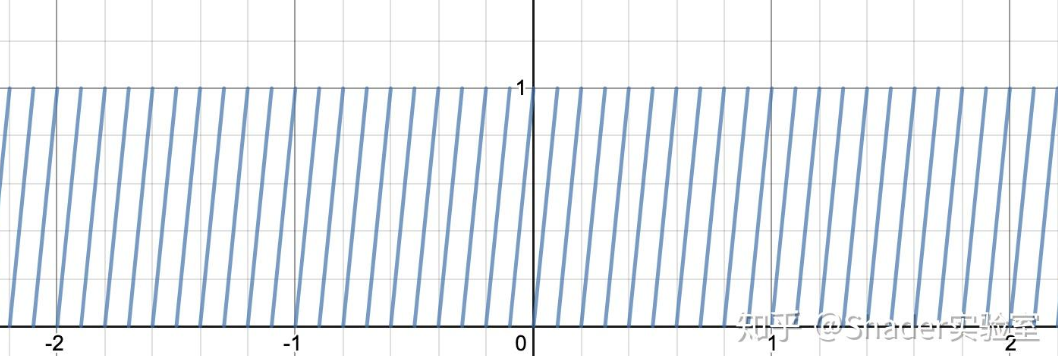

fract(1000x)的输出结果已经密到看不出图像规则了,我们可以对fract(10x)进行分析,从图像可以看出数字10代表单元格内出现的fract(x)的次数,那么fract(1000x)就表示单元格内出现了1000次的fract(x),当数字越大时值就越密,那么肉眼就越难分辨其变化规律,从而达到伪随机的效果:

这种带状输出虽然能在某个范围内达到随机效果,但是从宏观来看依旧能看出值的分布规律,解决方法是把随机值的范围限制为小数运算,再将其乘于大数。这里可以使用正弦函数进行范围限制,形如:
fract(sin(x) * 1000)

等等,看上去比fract(1000x)是好很多了,但是依旧能看出在某个范围内它是能呈现随机状态的。既然我们之前通过把fract(x)中的x乘上一个大数来制造伪随机的效果,用sin(x)乘上一个大数不是也同样能呈现伪随机的效果么?再配合fract函数,应该能呈现更加随机的状态。
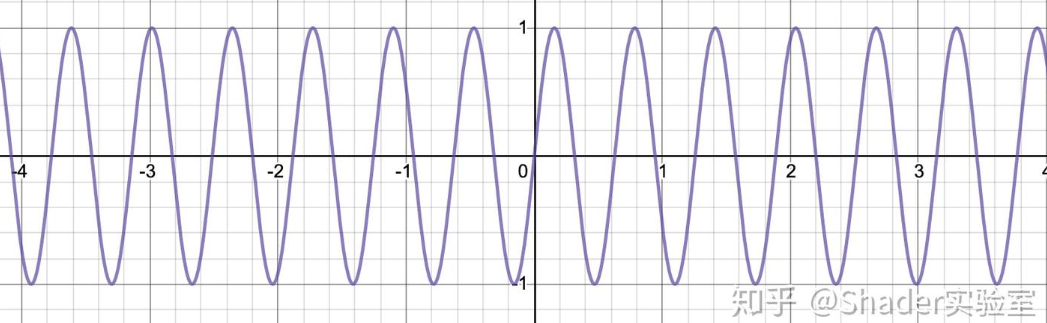
我们可以对fract(sin(x*1000) * 1000)进行绘制:

做到这里,图像输出看上去已经很随机了,虽然效果呈现上是随机的, 实际上它还是伪随机的算法,只要我们有精力去计算,总能预先知道某个位置的结果是怎样的。可那又如何呢,这不就是看脸的时代么?效果对了就好了,至于是否动刀还是天然美,又有什么关系。另外这里改成cos是否也可以呢?答案是肯定得,绝对没问题,这里的重点不是在于它是cos还是sin,而在于如何限制范围。
2D随机
在1D随机中已经解释了原理,2D随机只是对1D随机进行维度扩展,如:
fract(sin(dot(uv, vec2(28.323, 72.878))) * 10000.)
效果如下:

上面的效果是不是有点像小时候黑白电视机经常没信号时的效果?这就是White Noise。不好意思,暴露年龄。另外这里千万不要去计较vec2里是什么数值,这边数字为什么会是10000, 因为这数值是根据个人项目去调整的结果,合适自己的就行。(ps:有时候做技术真的不能钻牛角尖)。
感兴趣的伙伴们可以尝试实现下面的效果,过程可参阅“Shader实验室:极坐标系”,这里就不贴源码了。

什么?还有3D随机?告辞~~~ 本次实验就到这里啦,感兴趣的小伙伴可关注下面二维码。
