《点识成金AI》使用指南

阅读次数 681
learnearn

欢迎使用点识成金AI平台，以下是您需要了解的全面使用指南，包括主题类别、发布主题、AI使用指南、实名认证、声望兑换积分、积分提现、资产包子云盘扩容、VIP办理与积分购买、代码在线编译与预览，数学公式的添加等。

主题类别介绍

平台提供多种主题类别，以适应不同用户的需求：

  1. 问题主题：提出疑问，寻求解答。
  2. 积分问题主题：悬赏积分以吸引更专业的答案。
  3. 文章主题：分享见解或知识。
  4. 积分文章主题：通过积分激励创作者创作更优质的内容。
  5. 项目需求主题：发布合作项目，寻找合作伙伴。
  6. 云盘资源主题：在资产包子云盘上分享有用的文件或资料。

如何发布各主题

  • 登录账户：确保您已登录点识成金AI平台。

  • 选择主题类型：在导航栏选择“我要发布”并选择相应类别。
    image.png

  • 填写信息：输入标题、详细内容，添加相关标签或积分。

    • 发布问题时，您可以选择是否设置积分奖励。若设置积分，则为积分问题；若不设置，则为普通问题。当您的问题被其他用户回复并采纳，该用户将获得相应的积分。积分问题的发布会自动通知全站成员，以便您能够迅速获得答案。
      image.png

    • 发布文章时，您有权决定是否为文章附加积分权益。选择附加积分，您的文章将被归类为积分文章，读者需支付积分以阅读；若不附加积分，则文章为普通文章，对所有用户免费开放。您的积分文章若被阅读，将为您带来相应的积分收益。
      image.png

    • 发布项目需求时，您也可以选择是否设置积分奖励，当您的项目需求被其他用户回复并采纳，该用户将获得相应的积分。项目需求的发布也会自动通知全站成员，以便您能够迅速获得接受项目需求的人
      image.png

    • 发布云盘资源时，会跳转至资产包子云盘平台，具体可以查看平台内的云盘使用指南.pdf文件，对上传至云盘平台内的资源，用户可以选择公开分享，公开积分分享或私密分享，对于任何形式的公开分享，只要审核通过，分享的资源信息将会在点识成金AI中云盘资源主题专栏公开显示。
      image.png
      上述主题除了云盘资源主题，您都可以使用AI回复，以便更快获得答案及响应。具体可以查看AI使用指南

  • 提交审核：提交后，等待平台审核通过，用户也可以通过实名认证，实名认证成功后可简化审核的流程。关于提交的内容，用户需严格遵守用户协议上的条款避免违规。

AI使用指南

在提问或回复时，均可以使用AI回复开启辅助功能快速生成回复内容。

image.png

AI生成过程普遍较快，如果出现速度较慢的情况，用户可以先浏览其它内容，中断或浏览其它内容不会影响生成结果。
image.png

对于AI已经回复过的内容，会提示已经进行过AI回复。
image.png
对AI回复的内容可以追加回复，追加后的回复，可以继续让AI进行回复，AI会联系上下文，继续给出合理回复。
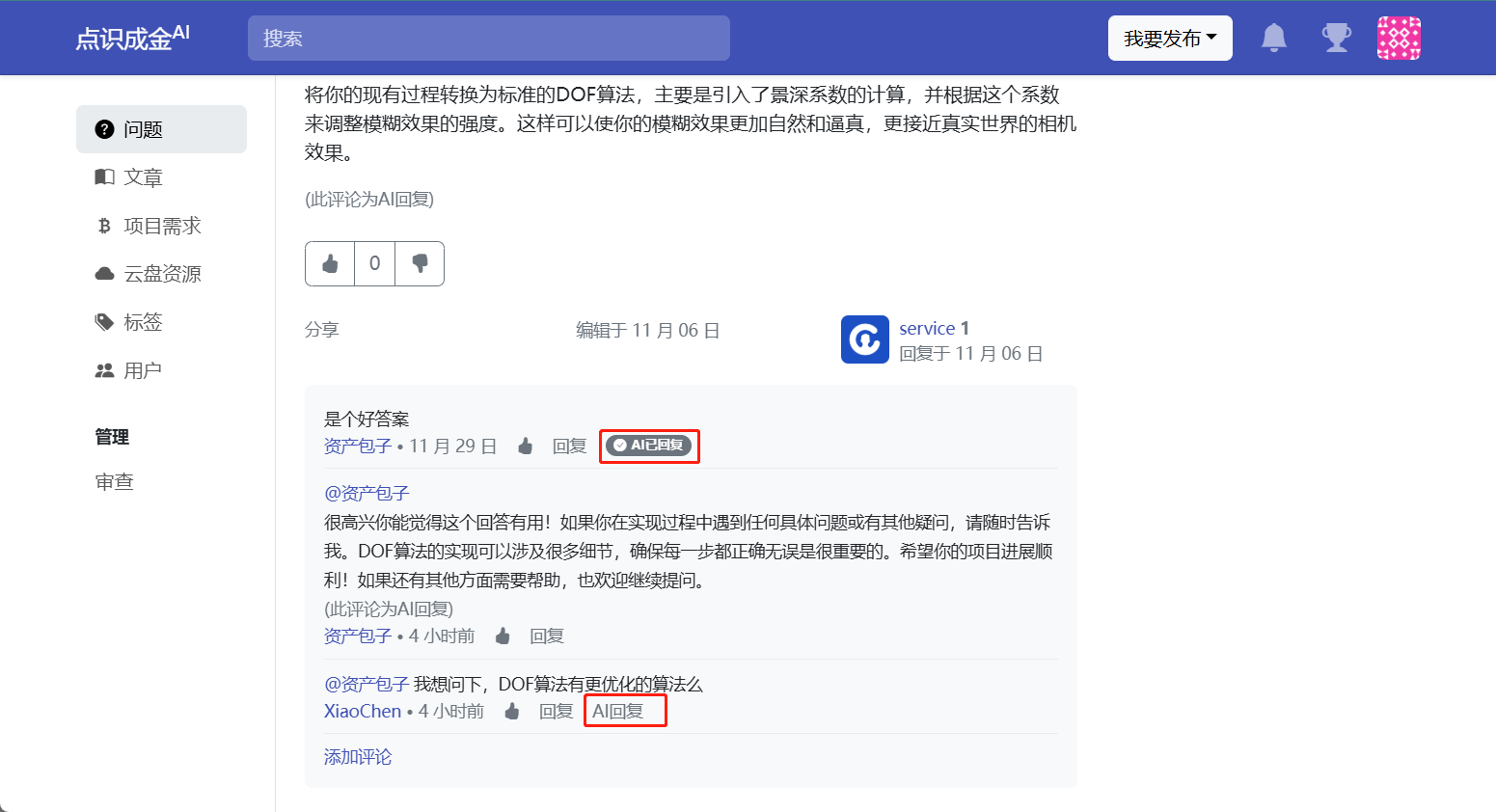
image.png

实名认证

实名认证是点识成金AI平台为了确保用户身份的真实性、安全性和交易的可靠性而实施的一项措施。通过实名认证，平台可以简化审核流程，提高用户体验与交易安全，并增强社区用户的信任度。

实名认证的流程
登录账户：确保您已登录点识成金AI平台。
实名认证选项：在点击个人头像找到“实名认证”选项，点击进入。
image.png
上传身份信息：我们通过支付宝平台进行实名认证信息填写，包括(支付宝登录账号，身份证ID，身份证姓名及绑定的支付宝手机号)
image.png

声望兑换积分

声望兑换积分是平台中一项重要的功能，它允许用户通过参与平台主题发布、参与主题回复或项目需求等方式将积累的声望值最终转换为积分。我们在这给出了声望兑换积分的详细信息：声望兑换积分的详细说明

积分提现

积分提现是点识成金AI平台提供的一项服务，允许用户将账户中的积分转换为现金，并提取到个人的银行账户或支付账户。以下是积分提现的具体流程和规则：

提现流程

  • 登录账户：用户需要登录到点识成金AI平台。

  • 进入提现页面：点击个人头像找到积分提现的选项，点击进入提现页面。
    image.png

  • 绑定支付账户：在申请提现前，用户需要完成实名认证并绑定支付宝账户, 以便提现金额能够顺利转入。
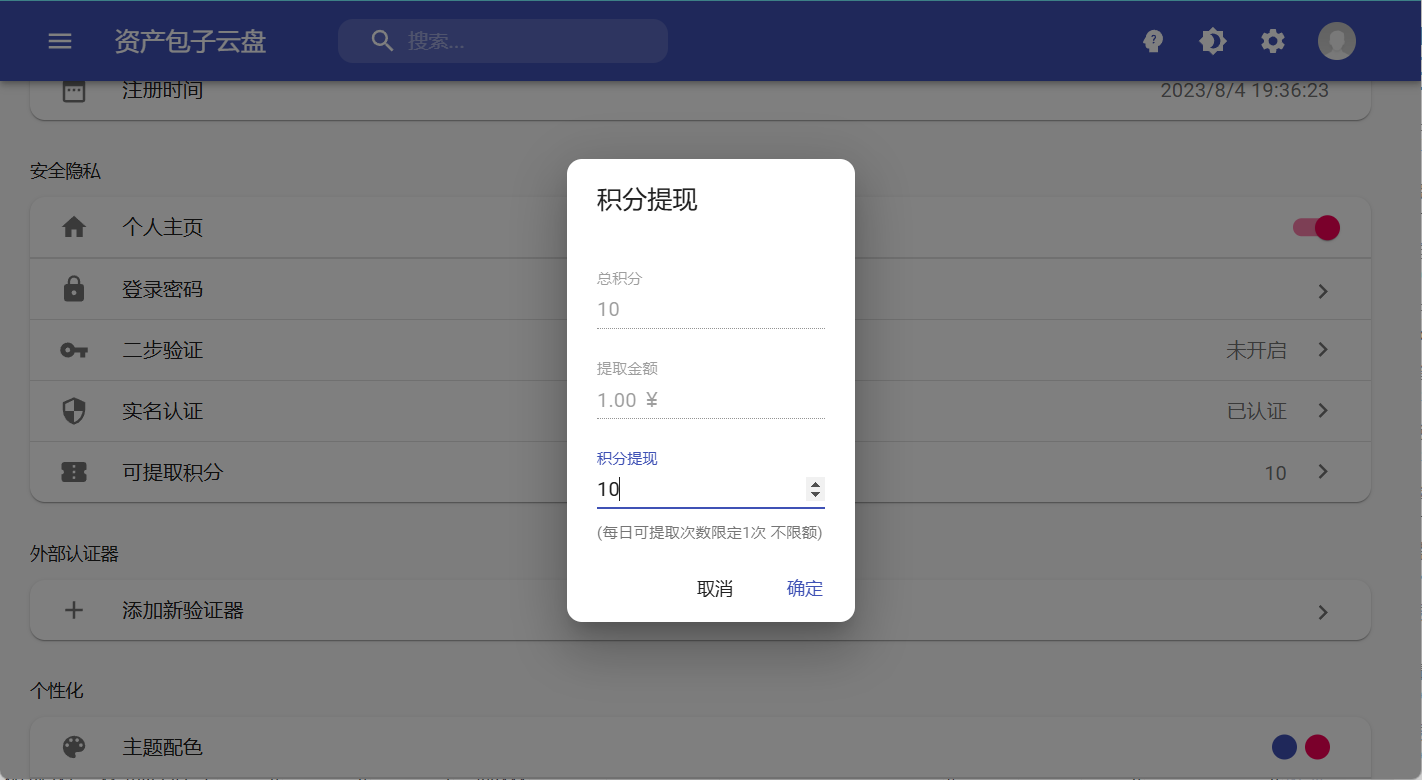
    image.png

  • 输入提现金额：用户可以根据账户中的积分余额，输入想要提现的金额。目前平台0.1¥≈1积分。

  • 提交提现申请：确认提现信息无误后，提交提现申请。提交提现申请后，系统会进行快速审核，审核通过后提现金额会快速到账。

资产包子云盘扩容

我们已经对资产包子云盘进行了全面升级，基础容量已从早期的500MB升级到了5GB，如果空间对您来说依旧不足，我们提供了更加优惠的扩容方案，可点击云盘扩容进行。

VIP办理与积分购买

用户可以点击办理会员链接成为VIP会员，用户不仅能够享受到更多的优惠和服务，还能在社区中获得更多的特权。具体的VIP权益可能会根据平台政策的变化而有所调整，建议用户定期查看平台官方的最新公告以获取最新的VIP权益信息。
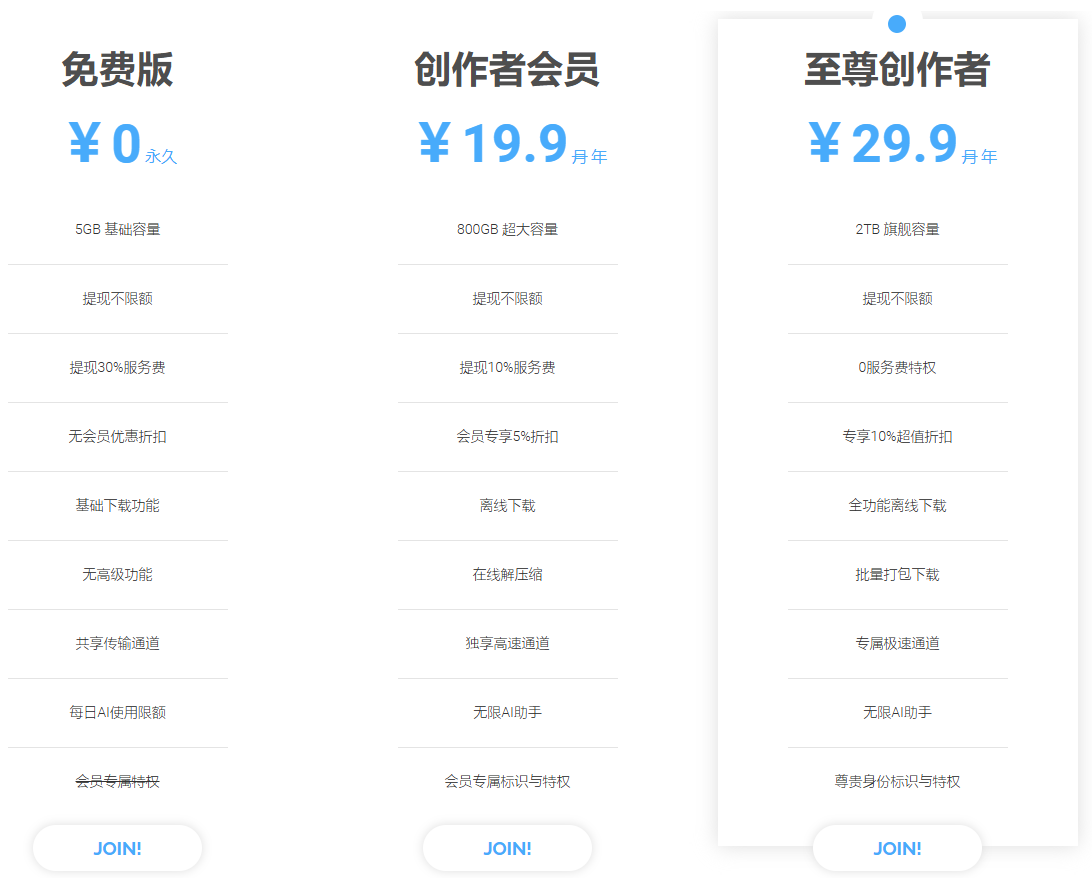
image.png

VIP专属折扣

  • VIP会员在查看或下载积分文章和资源时，可以享受专属折扣，降低查看和下载的成本。
  • 用户通过平台获得的积分收益，在提现或使用时会扣除规定的平台费用。
  • VIP会员可以享受部分费用减免，具体减免比例根据VIP等级而定。

积分充值
平台上的某些专题内容，包括但不限于特定主题的发布、查看和下载，均需通过积分支付来完成。例如，针对项目需求与积分问题的发布、积分文章的阅读以及积分资源的下载等操作，用户必须先购买相应的积分（VIP会员享受专属折扣）。当用户的账户积分不足以支持上述操作时，可通过以下链接进行充值：积分充值。此外，用户通过平台获得的收益，在扣除一定比例的平台服务费后将以积分形式返还至账户（VIP会员可享有部分平台费用减免优惠）
image.png

代码在线编译与预览

平台集成了一个全面的计算机编程知识体系，并特别为编程爱好者和专业人士提供了在线代码编译与预览的功能。针对图形编程，我们支持如ShaderToy和GLSL等着色语言的即时编辑与渲染。用户可以轻松定义和编写ShaderToy或GLSL代码，并直接将这些代码添加到专门的代码编辑面板中。一旦代码被输入或粘贴到面板内，系统会自动进行编译，并实时在预览窗口中展示效果，让用户能够立即看到自己的代码成果，极大地提升了知识分享的效率和体验。

  • 点击代码块
    image.png

  • 选择shadertoy添加代码块
    image.png

  • 即可编译与运行

float neLength(vec2 p, float l) {
    return pow(
        pow(abs(p.x), l) + pow(abs(p.y), l)
    	, 1.0/l);
}

float dSphere(vec3 p, float r) {
    return length(p) - r;
}

float dTorus(vec3 p, vec2 t) {
    vec2 d = vec2(length(p.xz) - t.x, p.y);
    return length(d) - t.y;
}

float dCircleTorus(vec3 p, vec2 t) {
    vec2 d = vec2(length(p.xz) - t.x, p.y);
    return neLength(d, 8.) - t.y;
}

float dBoxTorus(vec3 p, vec2 t) {
    vec2 d = vec2(neLength(p.xz, 8.) - t.x, p.y);
    return neLength(d, 8.) - t.y;
}

float dSegment(vec3 p, vec3 a, vec3 b, float r) {
    vec3 pa = p - a;
    vec3 ba = b - a;
    float h = clamp(dot(pa, ba)/dot(ba, ba), 0.0, 1.0);
    return length(pa - ba*h) - r;
}

vec2 opU(vec2 a, vec2 b) {
    return a.x < b.x ? a : b;
}

void rotate(inout vec2 p, float a) {
    float s = sin(a);
    float c = cos(a);
    
    p = mat2(c, s, -s, c)*p;
}

vec2 map(vec3 p) {
	vec2 p1 = vec2(p.y + 2.4, 0.0);
    p.y -= .6;
	rotate(p.xz, iTime);
    p.x -= 2.5;
    rotate(p.xy, 0.3*cos(2.0*iTime));

    vec2 w = vec2(dSphere(p, .70 - 0.1*sin(10.0*p.x + 5.0*iTime)*sin(10.0*p.y)*sin(10.0*p.z + 5.0*iTime)), 1.0);
    float radius = .15 - 0.1*smoothstep(2.3, 2.4, p.y > 0. ? p.y : abs(p.y + .4));
    vec2 sp = vec2(dSegment(p, vec3(0, 2.4, 0), vec3(0, -3.0, 0), radius), 7.0);
    rotate(p.zy, 3.14/2.0);
    vec2 bt = vec2(dCircleTorus(p, vec2(1, .08)), 2.0);
    for(int i = 0; i < 4; i++) {
        rotate(p.xy, iTime + float(i));
        p = p/1.2;
        vec2 bts = vec2(dCircleTorus(p, vec2(1, 0.08))*1.2, 3.0 + float(i));
        bt = opU(bt, bts);
    }
    
    return opU(p1, opU(opU(w, sp), bt));
}

vec2 spheretrace(vec3 ro, vec3 rd, float tmin, float tmax) {    
    float td = tmin;
    float mid = -1.0;    
    
    for(int i = 0; i < 256; i++) {
        vec2 s = map(ro + rd*td);
        
        if(abs(s.x) < 0.001 || td > tmax) break;
        
        td += s.x*0.5;
        mid = s.y;
    } 
    
    if(td > tmax) mid = -1.0;
    return vec2(td, mid);
}

vec3 normal(vec3 p) {
    vec2 h = vec2(0.01, 0.0);
    vec3 n = vec3(
        map(p + h.xyy).x - map(p - h.xyy).x,
        map(p + h.yxy).x - map(p - h.yxy).x,
        map(p + h.yyx).x - map(p - h.yyx).x
    );
    
    return normalize(n);
}

float shadow(vec3 p, vec3 l) {
    float res = 1.0;
    float td = 0.02;
    
    for(int i = 0; i < 256; i++) {
        float h = map(p + l*td).x;
        td += h*0.5;
        res = min(res, 32.0*h/td);
        if(abs(h) < 0.001 || td > 25.0) break;
    }
    
    return clamp(res, 0.0, 1.0);
}

vec3 lighting(vec3 p, vec3 lp, vec3 rd) {
    vec3 lig = normalize(lp);
    vec3 n = normal(p);
    vec3 ref = reflect(lig, n);
    
    float amb = clamp(0.7 + 0.3*abs(n.y), 0.0, 1.0);
    float dif = clamp(dot(n, lig), 0.0, 1.0);
    float spe = pow(clamp(dot(rd, ref), 0.0, 1.0), 52.0);
    
    dif *= shadow(p, lig);
    
    vec3 lin = vec3(0);
    
    lin += 0.4*amb*vec3(1);
    lin += dif*vec3(1, .97, .85);
    lin += spe*vec3(1, .97, .54);
    
    return lin;
}

vec3 material(float mid, vec3 p) {
    vec3 col = vec3(1.);
    
    if(mid == 0.0) {
        vec2 a = vec2(1)*smoothstep(-0.15, 0.15, mod(p.x, 2.))*smoothstep(-0.15, 0.15, mod(p.z, 2.));
        col = vec3(a, 1);
    }
    
    if(mid == 1.0) {
        col = vec3(.2, .8, .001);
    }
    
    if(mid >= 2.0 && mid < 7.0) {
        col = mix(
            vec3(1, .1, .1),
            vec3(.1, .1, 1),
            cos(mid + iTime));
    }
    
    if(mid == 7.0) col = vec3(.65);
    
    return col;
}

vec3 render(vec3 ro, vec3 rd, vec3 lp) {
    vec2 i = spheretrace(ro, rd, 0.0, 25.0);
    vec3 p = ro + rd*i.x;
    vec3 m = material(i.y, p);
    if(i.y == -1.0) return m;
    
    m *= lighting(p, lp, rd);
    
    return m;
}

mat3 camera(vec3 e, vec3 l) {
    vec3 rl = vec3(0, 1, 0);
    vec3 f = normalize(l - e);
    vec3 r = normalize(cross(rl, f));
    vec3 u = normalize(cross(f, r));
    
    return mat3(r, u, f);
}

void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
    vec2 uv = -1.0+2.0*(fragCoord/iResolution.xy);
    uv.x *= iResolution.x/iResolution.y;
    
    float s = 0.;
    if(iMouse.z > 0.) {
        s = 0.01*iMouse.x;
    } else {
        s = 3.1;
    }
    
    vec3 ro = 5.0*vec3(cos(s), 0.8, -sin(s));
    vec3 rd = camera(ro, vec3(0))*normalize(vec3(uv, 2.0));
    
    vec3 lp = vec3(.75, .75, 0);
    
    vec3 rend = render(ro, rd, lp);
    rend = pow(rend, vec3(.4545));
    fragColor = vec4(rend, 1.0);
}

数学公式

除了提供基本的排版功能外，我们还特别为内容创作者集成了数学公式的编辑支持。用户可以通过点击排版面板中的“数学公式”选项，按照提供的指南轻松插入和编辑复杂的数学表达式。这一功能使得技术文档、学术论文等需要精确数学表述的内容创作变得更加简单和直观，确保了数学公式的准确性和专业性。更多公式的写法可参考LaTeX数学公式指南。
image.png

我们将持续优化和扩展平台的工具链，致力于提升内容的质量与创作体验，为创作者带来更多的实质性价值。通过引入先进的功能和资源，我们旨在支持创作者更高效地创作，激发创新，并帮助他们实现更大的成功。

资产包子2043
0 Answers